钢悬链式立管涡激振动流固耦合非线性分析方法研究
刘 娟,黄维平
(1.中国海洋大学山东省海洋工程重点试验室,青岛 266071;2.青岛农业大学建筑工程学院,青岛 266009)
钢悬链式立管涡激振动流固耦合非线性分析方法研究
刘 娟1,2,黄维平1
(1.中国海洋大学山东省海洋工程重点试验室,青岛 266071;2.青岛农业大学建筑工程学院,青岛 266009)
随着油气资源勘探和开发活动不断向深海发展,钢悬链式立管(SCRs)成为深海浮式生产系统油气输送的首选立管,涡激振动是钢悬链式立管设计的核心问题。运用柔性索理论,采用具有弯曲刚度的大挠度细长梁模型模拟SCR,并根据提出的钢悬链式立管非锁定区考虑流固耦合的两向涡激振动模型,研究立管尤其是触地点处的涡激振动特性,算例表明,考虑流固耦合的两向涡激振动模型能够较好的模拟钢悬链式立管的涡激振动,可进行均匀流场中涡激振动的研究分析;钢悬链式立管触地点处的涡激振动响应较大且复杂,应作为SCR涡激振动研究的关键点。
钢悬链式立管;涡激振动;大挠度细长梁;触地点;流固耦合
海洋立管作为海面与海底井口的主要联系通道,既可用于浮式海洋平台,又可用于固定式平台及钻探船舶,是海洋石油开发的关键设备。钢悬链式立管(Steel Catenary Risers,SCRs)是近年来发展起来的一种新型深水立管系统[1],该立管克服了传统柔性立管及顶张力立管在深水应用的局限性,逐渐成为深水油气资源开发的首选立管系统[2]。由于钢悬链式立管是一个全新的概念,世界各国在各自独立研究的基础上开展了广泛的合作研究[3-4],如2H海洋公司发起的“深水钢立管”工业联合开发计划(STRIDE JIP)及MARINTREK、Statoil和NIG在众多投资商资助下发起的“钢悬链式立管-海床相互作用整体分析模型”工业联合发展计划(CARISIMA JIP)等,另外,巴西圣保罗大学在大量理论分析及实验研究基础上,提出了钢悬链式立管的数学模型[5],Silveira等[6]提出求解悬链式立管微分方程的数值方法,Moe等[7]分析了弹性伸长及弯曲刚度对钢悬链式立管静态位形的影响。
涡激振动(Vortex Induced Vibration,VIV)是钢悬链式立管设计的核心问题,由于钢悬链式立管的特殊几何形状和深水流场的复杂性,使钢悬链式立管的涡激振动分析比顶张力立管复杂的多。触地点作为立管悬垂段(sag bend)和流线段(flow-line)两部分的连接点,是钢悬链式立管涡激振动研究的特征点,其涡激振动特性是传统立管涡激振动研究中不曾遇到的问题[1]。随着水深的增加,深水立管的柔性越来越大,导致结构的涡激振动呈现不同的性能,而现有的涡激升力及涡激振动理论不能很好的解释圆截面柱体在稳定流场中的涡激振动现象,计算出的动态响应也与实际情况有较大出入[8-11]。
本文采用大挠度柔性索理论模拟钢悬链式立管,并基于深水立管结构振动与涡泄模式的相互影响,提出了钢悬链式立管非锁定区考虑流固耦合的两向涡激振动模型,进行钢悬链式立管尤其是触地点处的涡激振动及频谱特性分析。数值算列表明,考虑流固耦合的两向涡激振动模型能够较好的模拟钢悬链式立管的涡激振动现象,深水立管设计中,应考虑立管振动对其涡激振动特性的影响,钢悬链式立管触地点处涡激振动响应幅值较大且频率构成复杂,该点应作为钢悬链式立管涡激振动分析的关键点。
1 SCR大挠度细长梁模型
大挠度细长梁的运动分析是由Love等人于1944年首先提出的,后来经过Nordgren,Garrett,Paulling and Webster,Ma and Webster等人的改进,大挠度细长梁的运动方程更加完善[12]。该运动方程建立在图1所示的坐标系下,图中,梁的形状用向量r(s,t)表示,为梁变形后的弧长s及时间t的函数。ex、ey、ez表示随动坐标系与整体坐标x、y、z对应的单位矢量,n、b、t表示曲线s上一点的正法线、副法线和切线的单位矢量。假定梁的长度不可变化,即变形前后的弧长s不变。
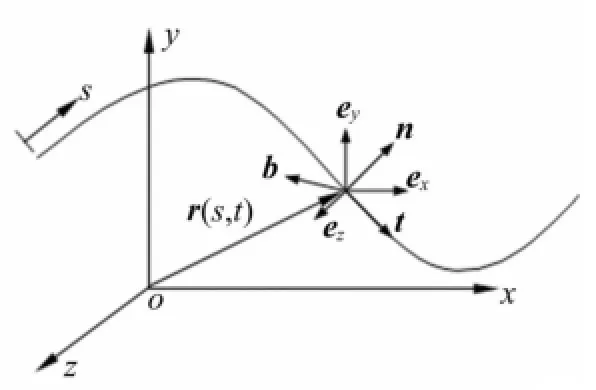
图1 大挠度细长梁的随动坐标系Fig.1 Coordinate system
根据动量和动量矩守恒定理,可得长为ds的梁平衡方程:
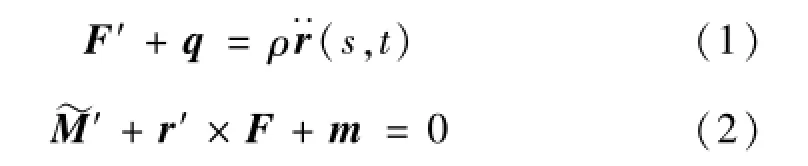
式中,F为梁截面的内力,~M为梁截面内力矩,q为梁上单位长度的分布外力,m为梁上单位长度的分布外力矩;ρ为梁单位长度的质量。梁截面内力矩~M(包括弯矩和扭矩)可表示为:
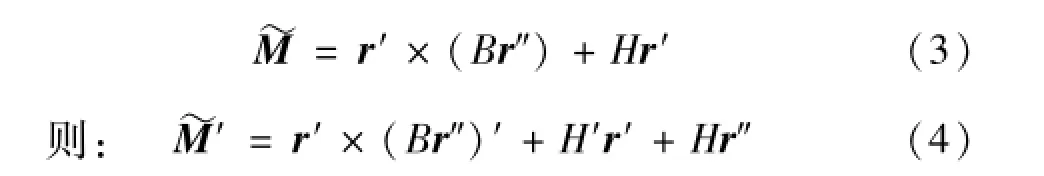
其中:B为梁弯曲刚度,H为扭矩。假定H=0,即忽略梁的扭矩,将~M′表达式带入式(2),若分布外力矩m=0,则:
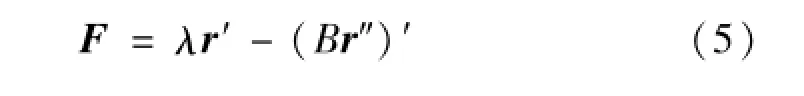
式中,λ为拉格朗日算子,λ=T(s,t)-Bκ2,其中,T(s,t)=r′·F为梁的截面张力,κ(s,t)为梁的截面曲率,κ2=-r′·r‴。
将式(5)代入式(1)得到大挠度细长梁的运动方程:
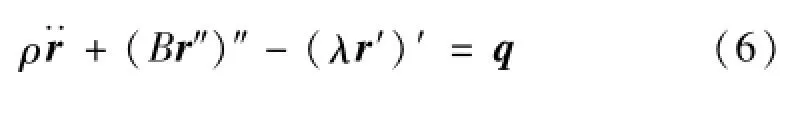
2 涡激振动模型
传统的涡激振动理论是建立在弱流固耦合基础上的,即圆柱体的振动幅度较小,因此可以把尾流处的流体看作固体,如尾流阵子模型。此外,传统的涡激振动主要关注的是横向振动,认为顺流向涡激振动的幅值相对较小,可以忽略,且顺流向涡激振动频率是横向振动的两倍。其涡激升力表达式为:
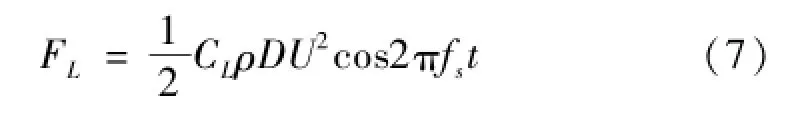
文献[13-14]通过模型试验研究了大柔性圆柱体的涡激振动,试验结果表明,管道模型的涡泄频率并不完全等同于Strouhal频率,在相同流速和管道直径的情况下,涡泄频率随管道模型固有频率的不同而有所不同,可见圆柱体的振动对涡泄频率有一定影响。另外,当振动处于锁定范围,顺流向幅值较小,模型的横向振动接近简谐振动,此时涡激振动的频率成分较少,且峰值接近Strouhal频率,该结论与传统的涡致振动理论一致;而当振动处于非锁定范围,模型的顺流向振幅达到与横流向同一量级,此时,模型的横向振动具有明显的随机特性,涡激振动的频率成分也增多,因此,圆柱体的顺流向振动对结构的漩涡脱落模式包括振幅和频率均有一定影响。
深水立管设计中,应尽量避免振动锁定以免产生共振现象,因此,非锁定区范围顺流向的振动以及流固耦合作用在立管设计中应予以充分考虑。将涡泄频率及涡激升力表达式中流场的速度项替换为流场与圆柱体的相对速度,则弹性圆柱体的涡旋泄放频率及涡激升力可修正为:
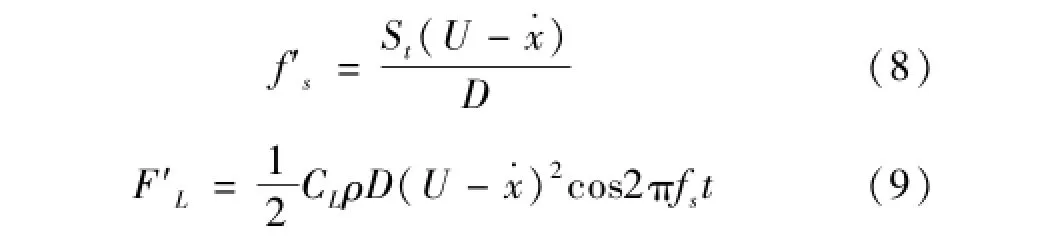
式中:x·为圆柱体顺流向速度,St为Strouhal常数,D为圆柱体直径,CL为升力系数,ρ为流体密度。由于结构振动产生的流固耦合作用,修正后的涡激升力模型是一个随圆柱体振荡而变频变幅的随机挠力。
式(8)和式(9)直观地反映了流固耦合效应,物理概念清晰,与试验结果吻合较好,如图2和图3所示,计算时,公式中的采用的是圆柱体顺流向响应的实测值。
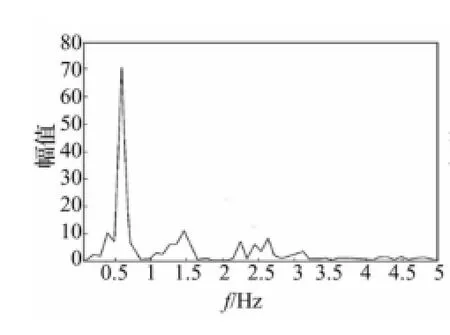
图2 计算涡激升力谱Fig.2 Calculated lift force spectrum
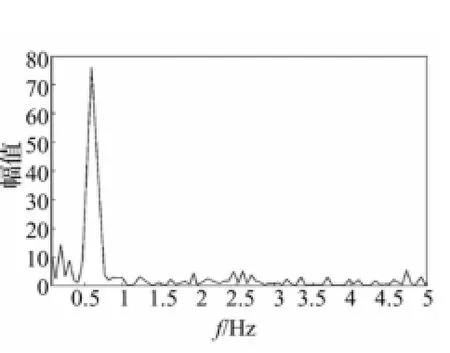
图3 实测涡激升力谱Fig.3 Measured lift force spectrum
基于修正的涡泄频率及升力模型,本文提出了一个深水钢悬链式立管非锁定区内考虑流固耦合的两向涡激振动分析模型:
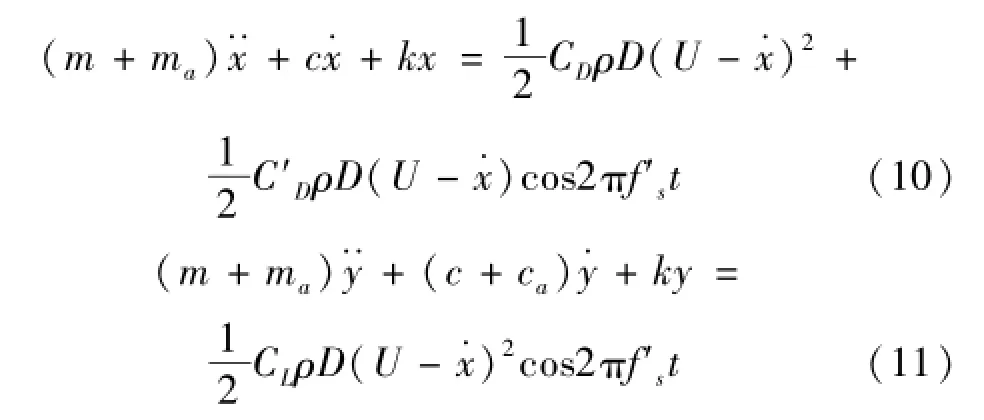
式中:x为顺流向弯曲挠度,y为圆柱体横向弯曲挠度,m,c及k分别为圆柱体单位长度的质量、阻尼及刚度,CD为拖曳力系数,C′D为顺流向的脉动拖曳力系数,CL为升力系数,ma和ca分别为附加质量和附加阻尼。
3 数值模拟
钢悬链式立管动力分析程序CABLE3D是2002年由美国A&M大学的Chen等[12]应用Fortran语言开发的三维非线性有限元分析程序。该程序基于大挠度柔性索理论,采用具有弯曲刚度的大挠度细长梁模型来模拟钢悬链式立管,可求解SCR的静力平衡位形及动力响应问题,具有较好的鲁棒性和有效性。
本文运用CABLE3D计算钢悬链式立管的静力位形及立管在均匀流场中的涡激振动响应,并根据本文提出的两向流固耦合涡激振动模型在CABLE3D基础上开发分析程序VCP_CABLE,计算考虑流固耦合的钢悬链式立管两向涡激振动时程响应,重点分析立管触地点处的振动响应,并对其作出谱分析,验证模型的可行性。
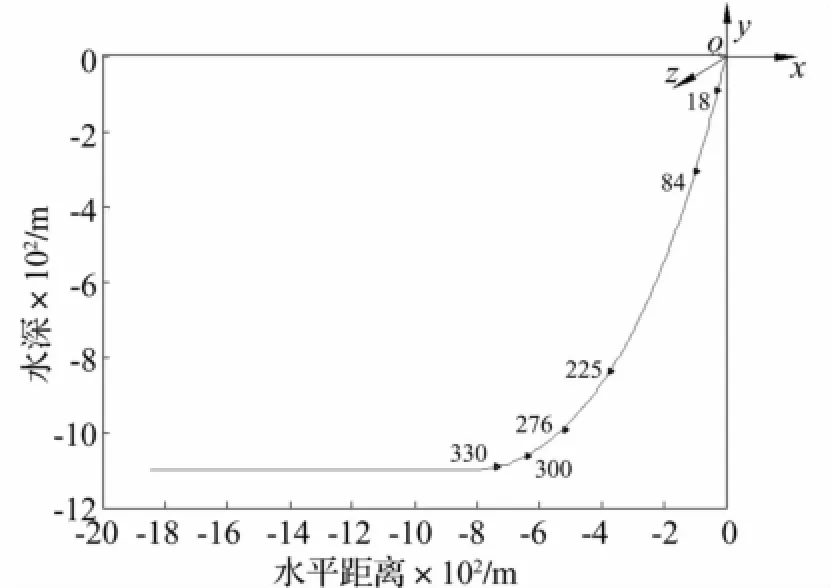
图4 SCR静平衡位形Fig.4 Static configuration of the SCR
本文模拟的钢悬链式立管外径为0.355 m,壁厚为0.025 m,设计总长为2 500 m,设计水深为1 100 m,悬挂点为铰接,井口距平台悬挂点的水平距离为1 846m,其它主要物理参数列于表1。图4为CABLE3D的静力分析部分模拟的该立管预张力为2 100 kN时的静力位形,此时SCR顶端与水深方向的夹角为16°。
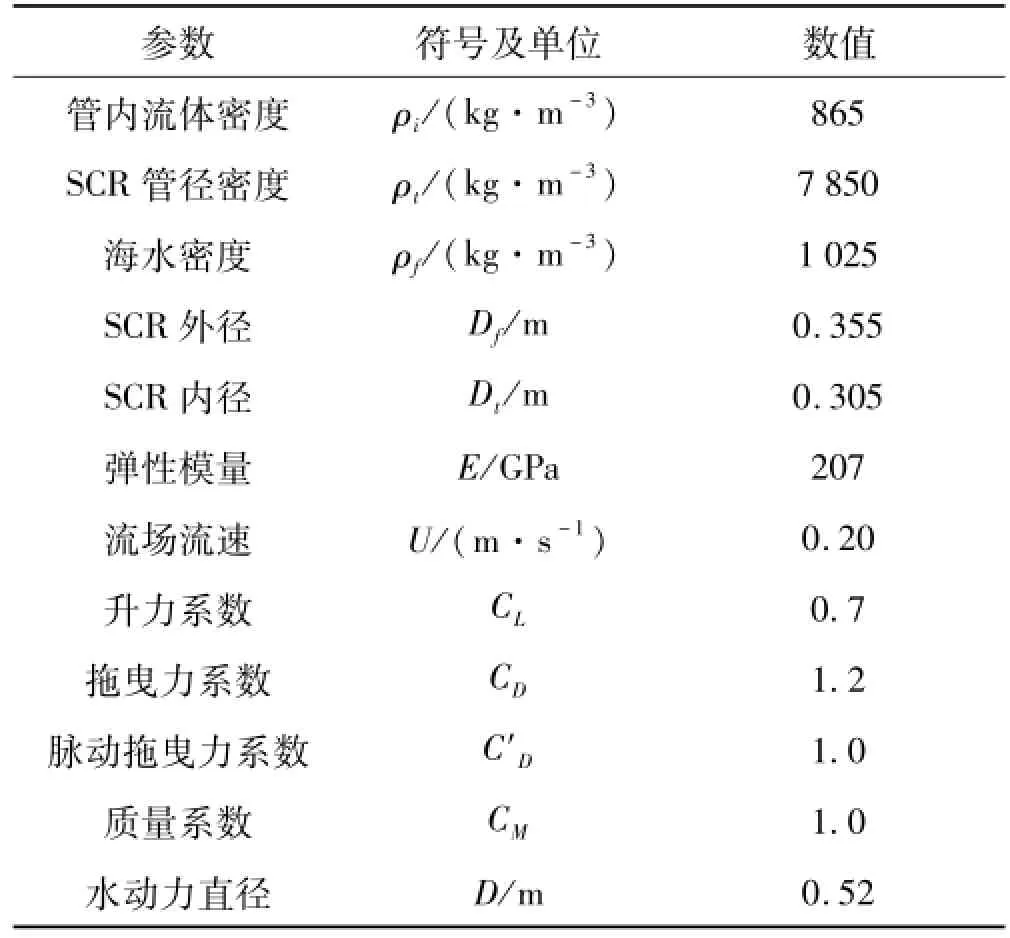
表1 SCR主要物理参数及流场参数Tab.1 Key parameters of the SCR and current
该立管设计海流流速为0.20m/s,来流位于立管初始平面内,即沿x轴方向。取Strouhal常数St=0.2,其它流场参数见表1,本文不考虑波浪作用。运用CABLE3D程序计算该立管的顺流向位移及流致横向涡激振动响应,本文选取立管上6个特征点进行分析,各点在立管中的位置见图4,可以看出18节点位于立管的悬挂点区域,84和225节点位于立管中部,276、300及330节点位于立管的触地点区域。图5~8分别为立管第18及330节点顺流向位移及横向涡激振动响应时程。
从图5及图7可以看出,顺流方向,立管在海流拖曳力作用下沿流向有一个波动,然后趋于平衡,平衡位置较初始位置稍有偏移。横流向则在简谐涡激升力作用下产生基本规则的振动响应,如图6和图8,响应的频率即为Strouhal频率0.076 9,响应幅值分别为0.028 m及0.072m,其余各点的响应幅值列于表2,从表中可以看出,立管悬挂点处响应幅值较小,中部的响应达到整个立管的最大值,立管下部开始减小,但触地点处的振动响应幅值再次增大,330节点的响应幅值是18节点的近3倍,可见,虽然触地点处的振动响应不是整个立管的最大值,却处于一个局部峰值,而触地点作为立管与海床接触点,其较大的涡激振动响应是引起钢悬链式立管疲劳损伤的重要因素。

表2 立管涡激振动响应幅值Tab.2 The response amplitude of VIV
图9和图10为运用分析程序VCP_CABLE计算的立管第18节点考虑结构振动及流固耦合的两向涡激振动时程曲线中初始振荡后的平稳部分,从图中可以看出,考虑流固耦合后,立管两方向涡激振动均为围绕平衡位置的随机振动。比较图10及图6可以看出,考虑流固耦合时立管横向振幅较未考虑时的振幅偏小,但此时立管顺流向振动振幅与横向处于同一数量级。图11和图12为第18节点振动平稳后两向涡激振动的响应谱曲线,可以看出两向振动的频率峰值均为0.073左右,表明立管在非锁定区两向涡激振动的频率大致相同,该频率值略低于该工况下的Strouhal频率0.076 9,且幅值频率的带宽较大,说明涡激振动具有较强的随机性。
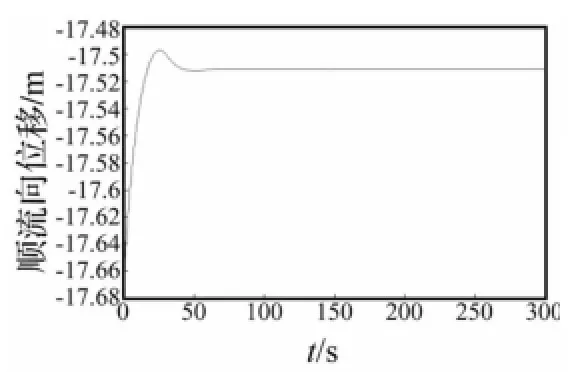
图5 立管第18节点顺流向位移Fig.5 The in-line displacement of the 18thnode

图6 立管第18节点横向涡激振动响应时程曲线Fig.6 The cross flow VIV response history of the 18thnode
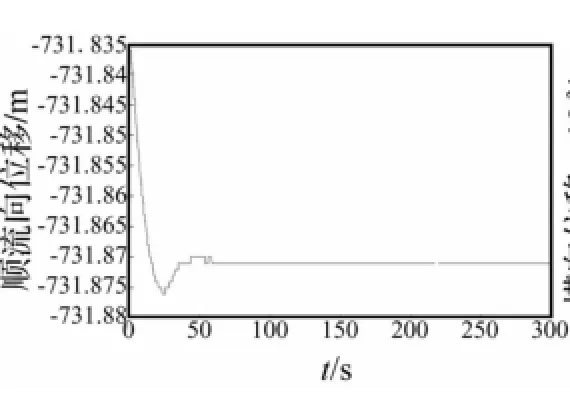
图7 立管第330节点顺流向位移Fig.7 The in-line displacement of the 330thnode
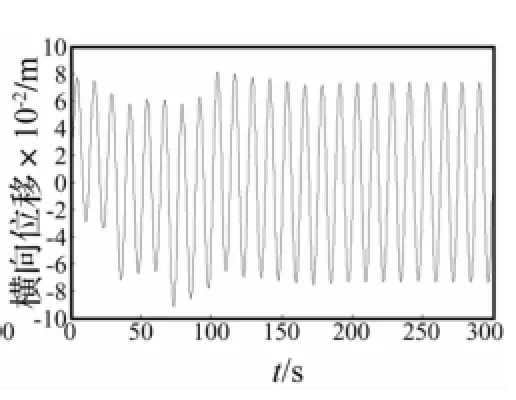
图8 立管第330节点横向涡激振动响应时程曲线Fig.8 The cross flow VIV response history of the 330thnode
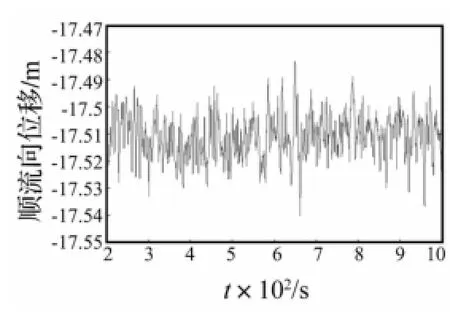
图9 立管第18节点的顺流向涡激振动响应时程Fig.9 The in-line response history of the18thnode
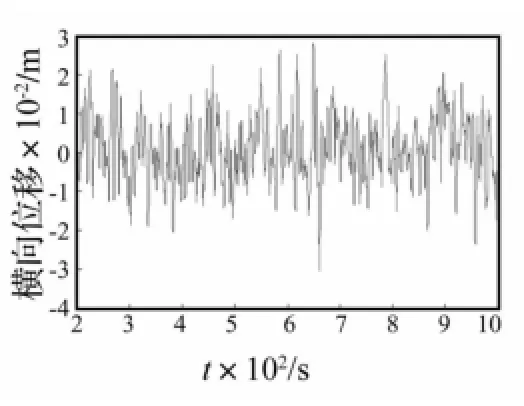
图10 立管第18节点的横向涡激振动响应时程Fig.10 The cross flow response history of the 18thnode
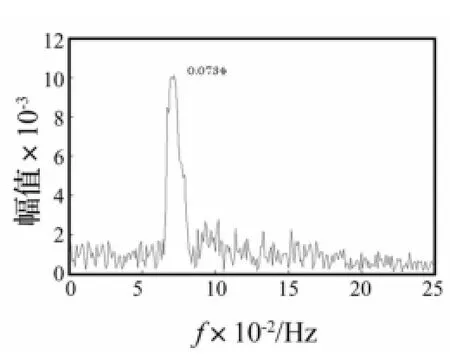
图11 立管第18节点顺流向涡激振动响应谱曲线Fig.11 Spectrum of in-line response of the 18thnode
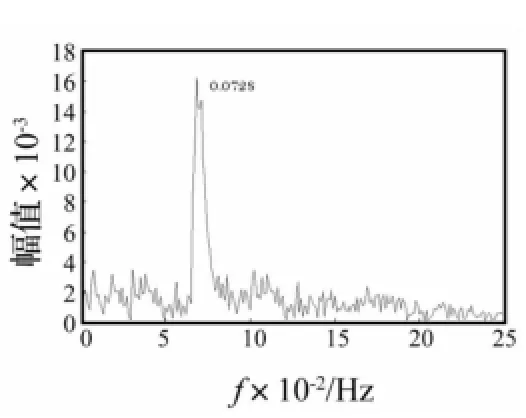
图12 立管第18节点横向涡激振动响应谱曲线Fig.12 Spectrum of cross flow response of the18thnode
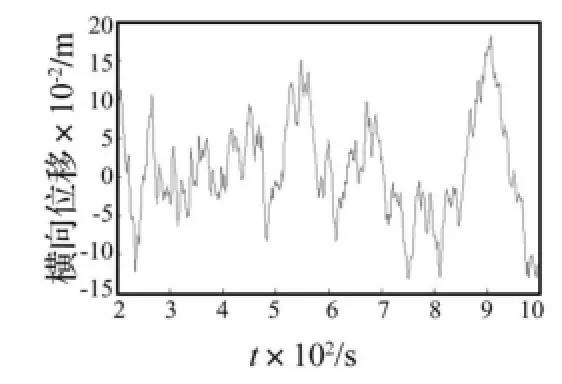
图13 立管第276节点的横向涡激振动响应时程Fig.13 The cross flow VIV history of the 276thnode
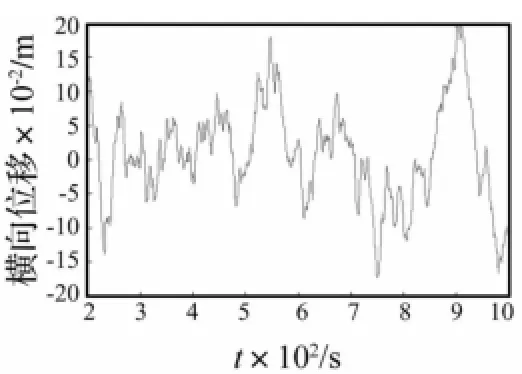
图14 立管第300节点的横向涡激振动响应时程Fig.14 The cross flow VIV history of the 300thnode
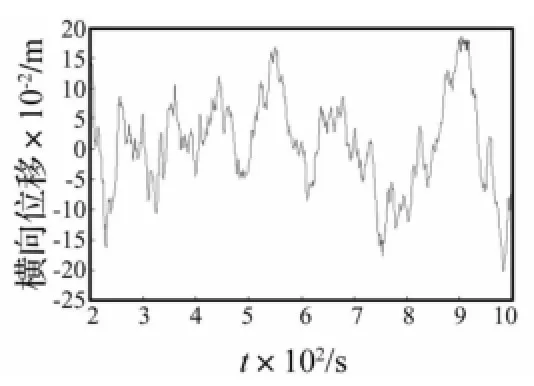
图15 立管第330节点的横向涡激振动响应时程Fig.15 The cross flow VIV history of the 330thnode
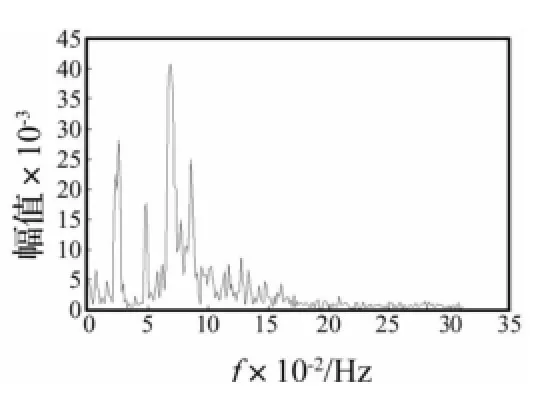
图16 触地点处横向涡激振动响应谱曲线Fig.16 Spectrum of cross flow response of TDP area
图13~15为运用VCP_CABLE计算的立管第276、300及330节点即触地点附近的横向涡激振动响应时程曲线,从图中可以看出,立管触地点处的横向振动比较复杂,除了涡激振动响应频率的小幅振动外,还存在低频大幅的振动,最大位移能够达到0.2 m左右,接近于一倍管径,该区域的响应复杂性也能从图16立管第330节点横向涡激振动响应谱曲线中看出,因此,钢悬链式立管触地点处响应幅值较大,且频率构成复杂,该区域在钢悬链式立管涡激振动的研究中是个十分关键的问题。
4 结 论
随着水深的增加,深水立管的柔性越来越大,大变形及强流固耦合作用使深水立管的涡激振动具有强烈的非线性性质,远远超出了传统圆柱体涡激振动研究所涉及的范围。本文采用大挠度柔性索理论模拟钢悬链式立管,并在前人研究的基础上提出了钢悬链式立管非锁定区考虑流固耦合的两向涡激振动模型,运用该模型研究钢悬链式立管尤其是触地点处的涡激振动问题。算列表明,结构振动及流固耦合作用对深水立管涡激振动具有一定的影响,在立管设计中应充分考虑;钢悬链式立管触地点处的涡激振动响应虽然不是整个立管的最大值,却处于一个局部峰值,而且其振动响应的频率构成比较复杂,除了存在涡激振动响应幅值外,还存在低频大幅值的成分,因为触地点在立管振动过程中不断与海底相互作用,其较大的响应及复杂的频率构成决定着钢悬链式立管的疲劳寿命,因此在钢悬链式立管涡激振动研究中是一个无法回避的问题,应该引起学术界的足够的重视。另外,本文仅是对钢悬链式立管触地点处的涡激振动情况进行初步的探讨,更为深入的了解触地点处的涡激振动特性还有待进一步的研究。
[1]黄维平,白兴兰,李华军.国外深水钢悬链线立管研究发展现状[J].中国海洋大学学报,2009,39(2):290-294.
HUANGWei-ping,BAIXing-lan,LIHua-jun.State of the art of research and development of overseas deepwater steel catenary risers[J].Periodical of Ocean University of China,2009,39(2):290-294.
[2]白兴兰.基于惯性耦合的深水钢悬链式立管非线性分析方法研究[D].青岛:中国海洋大学,2009:38-48.
[3]Hatton S A,Willis N.Steel catenary risers for deepwater environment[A].Proceedings of Offshore Technology Conference[C].Houston,USA,OTC,1998,OTC8607.
[4]Giertsen E,Verley R,Schroder K.A catenary riser/soil interactionmodel for global riser analysis[A].Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering[C].Vancouver,Canada,ASME,2004,23(1):633-640.
[5]Martins C A,Higashi E.A parametric analysis of steel catenary risers:fatigue behavior near the top[A].Proceedings of the International Offshore and Polar Engineering Conference[C].Seattle,USA,ISOPE,2000,2:54-59.
[6]da Silveira LMY,de Arruda Martins C.A numericalmethod to solve the static problem of a catenary riser[A].Proceedings of International Conference on Offshore Mechanics and Arctic Engineering[C].Vancouver,Canada,OMAE,2004,1:693-702.
[7]Moe G,Arnisen O.An analytic model for static analysis of catenary risers[A].Proceedings of the International Offshore and Polar Engineering Conference[C].Stavanger,Norway,ISOPE,2001,2:248-253.
[8]黄旭东,张 海,王雪松.海洋立管涡激振动的研究现状、热点与展望[J].海洋学研究,2009,27(4):95-100.
HUANG Xu-dong,ZHANG Hai,WANG Xue-song.An overview on the study of vortex-induced vibration of marine riser[J],Journal of Marine Sciences,2009,27(4):95-100.
[9]Sanchis A,Sælevik G,Grue J.Two-degree-of-freedom vortex-induced vibrations of a spring-mounted rigid cylinder with low mass ratio[J].Journal of Fluids and Structures,2008,24(6):907-919.
[10]Xu J,He M,Bose N.Vortex modes and vortex-induced vibration of a long,flexible riser[J].Ocean Engineering,2009,36(6-7):456-467.
[11]Lie H,Kaasen K E.Modal analysis ofmeasurements from a large-scale VIV model test of a riser in linearly sheared flow[J].Journalof Fluidsand Structures,2006,22:557-575.
[12]Chen X H.Studies on dynamic interaction between deepwater floating structures and their mooring/tendon system[D].Texas:Civil Engineering Department,Texas A&MUniversity,2002:15-28.
[13]黄维平,刘 娟,王爱群.基于实验的圆柱体流固耦合升力谱模型研究[J].工程力学,2012,29(2):192-196,204.
HUANGWei-ping,LIU Juan,WANG Ai-qun.A spectrum of the lift force on a cylinder with fluid-structure interaction based on experiment[J].Engineering Mechanics,2012,29(2):192-196,204.
[14]黄维平,王爱群,李华军.海底管道悬跨段流致振动实验研究及涡激力模型修正[J].工程力学,2007,24(12):153-157.
HUANG Wei-ping,WANG Ai-qun,LI Hua-jun,Experimental study on VIV of span of subsea pipeline and improved model of lift force[J].Engineering Mechanics,2007,24(12):153-157.
Fluid-structure interaction analysis for VIV of steel catenary risers
LIU Juan1,2,HUANGWei-ping1
(1.Shandong Key Laboratory of Ocean Engineering,China Ocean University,Qingdao 266071,China;2.College of Civil Engineering,Qingdao Agricultural University,Qingdao 266009,China)
With exploration of oil and gas in deep sea,steel catenary risers(SCRs)become the preferred riser systems for oil and gas import and export.Vortex induced vibration(VIV)is the key problem in design of SCRs.Here,SCRs were modeled into slender beams with large deflection and bending stiffness.The two-way VIV model with fluidstructure interaction was proposed,the VIV behavior of SCRs,especially,that at touch down points(TDP)was then studied based on the improvedmodel.The cases studies showed that themodel can be used to simulate the VIV of SCRs pretty well and to analyze the VIV of deepwater risers in uniform flow field;The VIV response of SCRs at TDP is larger and complex,it should be taken as a key point for the VIV study of SCRs.
steel catenary riser(SCR);vortex induced vibration(VIV);slender beams with large deflection;touch down point;fluid-structure interaction
P751
A
国家自然科学基金(51079136,51179179,51239008)
2013-02-07 修改稿收到日期:2013-04-01
刘 娟女,博士生,讲师,1977年12月生
黄维平男,教授,博士生导师,1954年3月生

