兆瓦级风力发电机组偏航反时限优化控制

徐卫峰 赵刚 郝勇生 严伟

(南京南瑞继保电气有限公司电气研究院,江苏 南京 211106)

兆瓦级风力发电机组偏航反时限优化控制

徐卫峰 赵刚 郝勇生 严伟

(南京南瑞继保电气有限公司电气研究院,江苏 南京 211106)

为解决兆瓦级风力发电机组不能频繁偏航和及时响应的矛盾,采用体现能量特征的反时限方法获得相对风向阈值及延时时间。考虑输入信号的稳定性,使用均值对风速和风向进行处理。在流程上对相邻两次动作进行时间限制,提高设备使用寿命。在PLC控制器上构建了仿真环境,实测结果验证了该算法的可行性及可靠性,为偏航系统优化运行提供可行指导。

风力发电机组 偏航控制 风向标控制 反时限 PLC

0 引言

随着各国对风力发电的大力支持,相关控制技术的研究也广泛开展起来。目前,研究主要集中在发电流程控制、变桨控制、变流器控制等[1]方面,在偏航方面也取得了一些成果。如基于风向标的风向标控制(vane control,V-C)[2],基于功率的爬山法H-C控制[3],及综合V-C和H-C的改进V-HC控制等[4]。此外,也出现了卡尔曼滤波的PI控制器、模糊控制器[5]、最优控制器等[6]。

上述算法和控制器对于兆瓦级以上的机组,虽理论上可行,但实际应用时存在一定的问题。如爬山法由于存在风速变化引起功率变化的情况,会触发偏航的尝试操作[7],该试探性的偏航操作是多余的。本文基于传统风向标控制,设计了一种反时限风向标控制(inverse time vane control,ITVC)算法,即通过反时限算法计算所需的偏差角度和延时,并采用改进的判断逻辑,取得了理想的预期效果。

1 ITVC算法

ITVC算法对原风向标控制算法中的相对风向阈值、偏航激活延时以及触发条件进行了改进。

1.1 风向标控制算法

风向标控制(V-C)算法的控制流程如图1所示。

图1 风向标控制流程图Fig.1 Flowchart of vane control

风向标控制就是根据安装在风机机舱尾部的风向标测得的相对风向差,通过判断风向偏差的大小来控制偏航,使得风机始终处于迎风状态的一种策略。由于具有控制流程简单、维护方便等特点,V-C算法在大中型风机上得到了广泛的应用。风向标有机械和超声波[8]两种类型,由于超声波风向标无机械结构,可靠性高,被广泛应用于风机。

由于结构和自重问题,在考虑设备使用寿命与自用电的情况下,大型风力发电机组不可能与小型机组一样可随时偏航保证对风,因此需合理规划启动偏航的时机,取得在发电量、设备使用寿命以及自用电三者之间的平衡,做到高风速下能及时响应、低风速下合理偏航。这取决与两个关键的因素,即启动偏航的相对风向的阈值和门槛越过后的延时。

1.2 相对风向阈值

相对风向的阈值决定了偏航系统什么时候被激活。该值的大小决定了偏航启动的频繁程度。文献[2]中由于传感器采样精度的问题,其阈值限制在了15°。近年高精度超声波风向标的大量采用,使该方案已经不能很好地满足实际需求。

偏航的目标是为了尽可能多地获取风能,但其自身运转需要消耗一定的能量,因而有必要评估不同工况下的偏差角带来的发电损失与自用电之间的关系,即通过偏航对风增加的发电功率需大于自用电功率。依据贝兹理论[9],风力发电机组的发电功率满足式(1):

式中:P为发电机组有功功率,W;ρ为空气密度,kg/m3; v为风速,m/s;S为风轮的扫风面积,m2;Cp为风能利用系数。

当风向存在偏差角θ(0～90°)时,有损失功率Ps:

当损失功率大于偏航自用电功率Pz时,则有必要进行偏航对风,获取最大能量,即Ps＞Pz。由此可得:

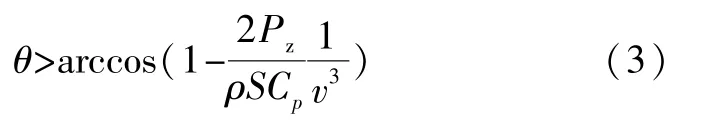
在风机型号固定及工况固定的情况下,通过式(3)可知θ与风速倒数的三次方成反余弦关系。由于式(3)比较复杂,有必要对其进行简化。设:

则式(3)可简化得到:

对于兆瓦级以上的风机,Pz取20 kW,ρ约为1.21 kg/m3,S以风轮半径50 m计算,Cp取0.48。因正常情况下风速在2 m/s以上对于启机才有意义,最终1/v′的取值在[0,1]之间,与1/v的区间匹配。

通过数据分析可知,偏差角与无量纲风速的倒数平方基本与原反余弦关系吻合,如图2所示。图中X轴为v0/v,为无量纲风速,其中v0为启动偏航的下限风速。

图2 偏差角与风速倒数的关系Fig.2 Relationship between difference angle and(v0/v)

根据上述关系,考虑只有v大于v0才有实际意义,设计偏差角θ满足以下表达式:

式中:a为常量,需根据风机系统的实际设计方案整定。

虽允许的偏差角θ取值范围为0～90°,但由于风向的波动性,为避免误动作,需设置一个下限。同理,如果该值较高,则有可能长时间都无法动作。因此,经过限值的编差角θ的实际取值曲线如图3所示。

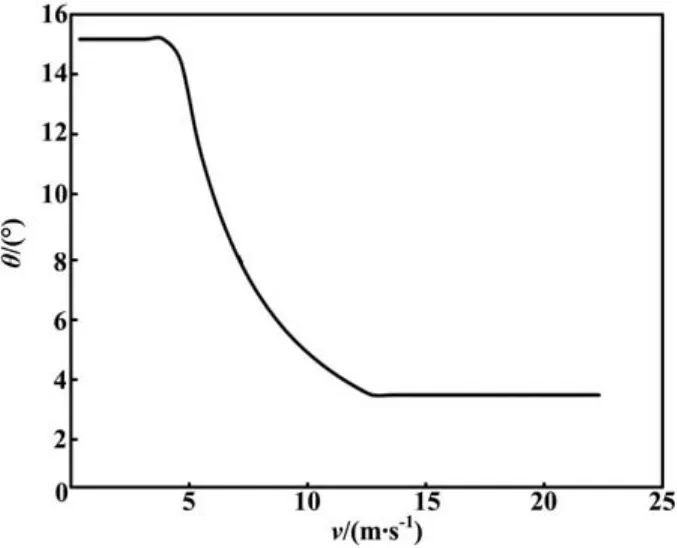
图3 偏差角θ实际取值曲线Fig.3 Curve of actual value taken of difference angle θ

1.3 偏航激活延时

当相对风向偏差角超过阈值时,即进入偏航激活状态。由于风向采样的扰动,因此有必要通过延时确保执行的准确性。但不同工况下采用固定延时一刀切的做法显然不符合实际运行的需要。高风速时风向的采样精度也较高,同时风机本体受到的侧向力的作用引起的振动也较大,此时可适当减少延时时间,以提高执行效率。

根据国际电工委员会标准(IEC 255-4)和英国标准规范(BS 142.1966)的规定,对反时限有以下定义:

式中:k为时间常数系数;Tp为时间常数;I为故障电流;Ip为基准电流;α为反时限类型,取值为0.2时表示为一般反时限,取值为1时表示为强反时限,取值为2时表示为超反时限,取值为3时表示为长反时限。

由于风速与电流一样都是能量的体现,且存在类似的指数关系,因而上述反时限方案完全适用于偏航启动的延时。考虑到相对风向采样值的波动性,选用较为缓和的一般反时限方案。根据式(7)即有以下关系式:

式中:β为时间常量,由风机偏航系统方案确定;v0为启动偏航的下限风速。

由式(8)可知,当v/v0在[1,∞]变化时,对应的t的取值为[0,∞]。实际使用时间不可能取0值,如取0值或极小的值,则失去了消除风向采样扰动的能力;也不能取很大的值,这样会导致偏航长时间满足不了启动条件而无法动作,从而失去了判断的意义。因而必须对该延时加以限制。启动偏航延时曲线如图4所示。

图4 启动偏航延时曲线Fig.4 Delay time curve of starting up yaw

1.4 ITVC算法的优点

相对风向阈值与偏航激活延时对传统的V-C控制进行了改进,主要体现在以下两个方面。

①合理捕获,风能最大化。通过对当前可捕获风能与自消耗能量之间的评估,合理做出启动偏航的判断,优化偏航系统的运行,提高偏航系统设备的使用寿命。

②快速的响应能力。利用反时限的原理,确保了条件满足情况下动作的快速性,缩短了对风时间,提高了总发电量。

2 程序设计

相对风向和风速采样值的处理是整个算法的基础,在程序设计时需确保其真实、可靠。另外偏航控制流程在一些细节方面同样需要关注。

2.1 相对风向和风速采样值处理

在整个对风算法中,除了相对风向阈值以及偏航激活延时的确定,采样值的准确度对于算法至关重要。而采样值精度是由选用的风向仪决定的。对于超声波风向仪,其采样值是快速波动的,加上可能出现的阵风和随机风[10]的影响,其瞬时采样值波动范围很大,这对于需要稳定可靠的偏航算法而言几乎无法应用。

由于随机性,各种滤波方法一方面难以取得理想效果,另一方面计算量也较大。常规的平均法虽简单直观,但为取得较好的滤波效果,就必须延长平均值计算的时间间隔。平均法由此带来一个采样值滞后问题,即有可能5 min的风向偏差平均值已经达到相对风向阈值,而当前实际的相对风向在可接受范围内,且已经稳定,不需要偏航。因此,需合理选取平均值时间间隔,通过长间隔加短间隔同时判断的方式增加阈值越限的准确性。

作为相对风向阈值和偏航激活延时计算的重要依据,风速同样采用平均值方法。其平均值计算时间窗可以适当取长一点,以充分反映当前的能量供给状态,但需同时考虑动态响应问题。

2.2 ITVC算法控制流程

在偏航系统运行过程中,除了解缆过程外,在正常偏航过程中,均通过液压系统使机舱带有一定的阻尼进行对风。这主要是为了保证机组在大风运行下的可靠性。但带载运行带来的磨损对机组寿命有着不利的影响。为限制机组频繁对风,可通过在两次偏航动作之间增加一个强制延时间隔,即下一次偏航动作必须在上一次偏航动作完成一定时间后进行。该策略在相对风向大范围扰动的情况下能有效降低偏航启动的次数。我们需根据机组本身特性确定该延时。

ITVC算法控制流程说明如下。首先,对风速和风向采样值进行平均值滤波处理,同时根据上述算法获得相对风向阈值以及偏航激活延时时间。在判断满足上次偏航结束延时后,将相对风向的偏差值与阈值进行比较。如果越限条件满足且延时时间到,则激活相应的偏航动作。当相对风向角度满足停止条件时,停止偏航并记录当前扭缆位置,最后返回。

经过改进的ITVC算法控制流程如图5所示。

图5 ITVC偏航控制流程图Fig.5 Flowchart of ITVC

3 仿真数据及分析

根据上述算法,在风速为7 m/s、相对风向阶跃为10°的情况下,偏航系统执行的曲线如图6所示。

由于风速是波动的,通过风速计算的相对风向阈值也是波动的,该值通过计算为7.6°左右。通过风速计算得到的延时时间也是一个变化量,该值通过计算为9.6 s左右。由图6可看出,当相对风向阶跃10°后,相对风向差30 s均值与1 s均值在9.1 s附近,同时大于阈值,并在开始时保持该状态。在18.7 s处,相对风向30 s均值开始下降,即顺时针偏航开始,整个延时过程持续约9.6 s,与设定值吻合。在36.8 s处,相对风向差1 s均值满足1°以内的要求,即停止偏航。

图6 偏航仿真动作曲线Fig.6 Yaw action curve in simulation

4 结束语

本文在传统风向标控制(V-C)偏航控制的基础上,提出了一种基于反时限的反时限风向标控制(ITVC)算法。该算法面向大中型风力发电机组,通过反时限特性有效提高了动作速度,并通过相邻两次偏航强制时间间隔,提供一种在效率与机组设备使用寿命之间的平衡策略,优化了相对风向阀值计算,在兆瓦级以上机组具有良好的控制效果和应用前景。

[1] 陈雷,邢作霞,潘建,等.大型风力发电机组技术发展趋势[J].可再生能源,2003(1):27-30.

[2] 季田,田德.浓缩风能型风力发电机迎风自动控制系统[J].太阳能学报,2003,24(1):90-93.

[3] Jacobson S H,Yucesan E.Analyzing the performance of gerneralized hill climbing algorithms[J].Journal Heuristics,2004,10(4): 387-405.

[4] 朴海国,王志新.风电机组偏航控制系统的新型算法——V-HC研究[J].太阳能学报,2008,29(8):1028-1033.

[5] 徐德,诸静.风力发电机风向随动控制系统[J].太阳能学报, 2000,21(2):186一191.

[6] Farret F A,Pfitscher L L,Bernardon D P.Sensorless active yaw control for wind turbine[C]∥Industrial Electronics Society,IECON′01.The 27th Annual Conference of the IEEE,2001:1370-1375.

[7] 陈亮,谭伟,田天,等.风力发电机组偏航控制研究[J].风机技术,2013(2):64-68.

[8] 王宇峰,裴科伟,于会勇.用于风力发电的超声波测风系统设计[J].风机技术,2012(4):53-55.

[9] 霍志红,郑源,左潞,等.风力发电机组控制技术[M].北京:中国水利水电出版社,2010:7-10.

Inverse Time Optimized Yaw Control for MW Wind Turbines

In order to resolve the contradiction between infrequent yaw and timely response for MW wind turbines,the inverse time method reflecting energy features is used to obtained relative wind direction threshold and time delayed.To ensure the stability of the input signal,the average of wind speed and wind direction is used.Service life of the equipment is improved by limiting the time period of two adjacent actions of the yaw.The simulation environment is built in PLC controller,the result of real tests verify the feasibility and reliability of this method;it offers feasible guidance to optimal operation of the yaw system.

Wind turbine Yaw control Vane Control Inverse time PLC

TP273+.1

A

修改稿收到日期:2013-12-14。

徐卫峰(1979-),男,2005年毕业于东南大学热能工程专业,获硕士学位,工程师;主要从事风机主控系统的开发及测试工作。