脉冲雷达自适应步进数字AGC设计与仿真
朱璐, 邹波, 江利中
(1.92941部队第120研究所,辽宁 葫芦岛 125001;2.上海无线电设备研究所,上海 200090)
脉冲雷达自适应步进数字AGC设计与仿真
朱璐1, 邹波2, 江利中2
(1.92941部队第120研究所,辽宁 葫芦岛 125001;2.上海无线电设备研究所,上海 200090)
模拟AGC数字化设计在雷达上的应用已成为必然趋势。文章在研究模拟AGC数字化设计的基础上,提出自适应步进、可调AGC带宽、兼具快速性和稳健性的脉冲雷达数字AGC控制算法。仿真和分析结果表明,算法响应速度快、性能较好,且通过调整增益衰减因子可以实现欠阻尼控制、调整α-β滤波的系数可以实现AGC带宽控制。
雷达;模拟;数字;自适应步进
0 引言
自动增益控制(AGC)是雷达中频接收的重要组成部分[1]。中频接收机设置自动增益控制的目的在于使接收机的增益随着信号的强弱进行调整,或者保持接收机的输出恒定在一定范围[2]。
AGC按实现方法分类,可分为模拟AGC和数字AGC[3]。模拟AGC由于模拟器件如检波器和RC电路的原因,在窄脉冲、高重频或环境温度变化条件下输出归一化电平难以控制、快速响应和稳定性不能兼顾。与模拟AGC相比,数字AGC可实现更为复杂的控制算法,并且数字AGC的响应和收敛速度更快、稳定性更好[2]。因此,随着雷达性能要求的提高和数字化技术的发展,模拟AGC的数字化设计已广泛应用到各型雷达[3-5]。
数字AGC的基本原理是对中频模拟信号进行数字化,然后估计信号的幅度,反过来控制前端中频放大电路中的可编程数控衰减器或模拟衰减器,将信号输出调整到适合检测的幅值范围内,或者控制输出的数字信号幅度稳定在一个恒定的值。本文在研究模拟AGC数字化的基础上提出自适应步进、可调AGC带宽、兼具快速性和稳健性的AGC控制算法。
1 模拟AGC的数字化设计
模拟AGC的控制产生部分采用模拟电路实现,如图1(a)所示,主要由输入放大器、检波器、低通滤波器和输出放大器几个部分构成。输入放大器有两个输入,其中一个输入信号Sin为接收机的输出,另一个输入信号为归一化电平U。检波器检出信号的功率,滤波器用来平滑检波输出信号中变化较大的部分[3]。

图1 模拟AGC和数字AGC原理框图
数字AGC的数字化设计如图1(b)所示,其增益控制执行部分与模拟AGC没有太大区别,主要区别是采用数字信号处理得到可控增益衰减器的控制电压(或信号)。所以模拟AGC数字化设计的关键就是实现增益控制算法。
2 数字AGC的算法实现
通过与模拟AGC的比较可知,数字AGC设计需要解决的主要问题有三个:
a)中频信号幅度/功率的估计;
b)增益控制策略;
c)AGC带宽控制。
2.1 中频信号幅度的估计
雷达中频接收机输出信号给信号处理机后,信号处理机需要通过数字检波方法估计该中频信号的幅度或功率,才能实时给中频接收机反馈相应的增益控制电压。
2.1.1 数字检波方法
中频信号幅度/功率的估计方法有两种:
a)直接处理中频数字信号得到信号的幅度/功率(中频信号数字检波);
b)通过信号处理过程中的基带I路和Q路信号检波得到信号的幅度/功率(数字基带数字检波)。
2.1.1.1 中频信号数字检波
直接处理ADC采样后的数字中频信号得到信号幅度/功率类似于模拟AGC的模拟检波,用数字检波的方法得到信号的包络,通常采用平方律检波[6]。
设数字中频信号为
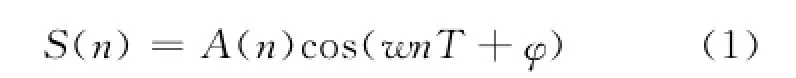
式中:A为信号幅度;w为信号数字角频率;T为信号采样周期;φ为信号的初始相位;n为采样点。
平方检波即可得到直流分量

通过C(n)即可估计中频接收机输出的中频信号的幅度/功率。
2.1.1.2 基带信号数字检波
基带信号数字检波通常用信号处理过程中得到的基带I路和Q路信号平方和来估计信号的幅度/功率。设信号处理过程中得到的正交基带信号分别为I(n)和Q(n),则平方检波后得到

通过C(n)即可估计中频接收机输出的中频信号的幅度/功率。
值得注意的是两种方法在处理的过程中都有滤波器等带来相应增益,但增益是固定的,可以通过数字补偿来直接得到模拟中频信号幅度/功率的估计值。
2.1.2 均衡滤波
上述两种方法估计的信号幅度/功率受噪声影响较大,如果直接利用估计结果得到AGC控制电压,则控制电压起伏较大,影响AGC的稳定性和响应时间。通常采用均衡滤波器滑动滤波每个采样点估计的信号幅度/功率[2]。对于脉冲雷达来说,可以取一个距离门(重频)内的最大值作为信号幅度/功率的估计值,如图2所示。

图2 信号幅度/功率估计的均衡滤波
图2中,左半部分为m阶的滑动均衡滤波器,右半部分为一个取最大值比较器。其中, x(n)为输入的采样信号幅度/功率,y(n)为对应的m采样点信号幅度/功率估计的最大值。

图3 滑动均衡滤波器设计
图3(a)为不同阶数滑动均衡滤波器对叠加噪声的正弦信号滤波后的结果,从图可以看出32阶的滤波器滤除效果比较接近原始信号,且滤波器的阶数相对较小。
图3(b)为32阶滑动均衡滤波器(系数为32:-1:1间隔-1归一化后取数)的幅频响应和相频响应,从图可以看出该滤波器为一线性相位的低通滤波器。
2.2 自适应步进的增益控制
得到中频信号的幅度/功率估计值后,需要根据此估计值和输出门限得到AGC的控制电压。设第k个回波(重频)中频信号功率估计值为,中频接收机要求的输出归一化信号功率为Pth(输出门限),则功率差为

设接收机输出信号功率为Pth时接收的中频回波信号功率为Pin,则对应的门限增益为

为将信号功率估计为Pˆk的信号通过AGC控制后输出为Pth的信号,增益变化为

设k时刻到k+1时刻增益调节为ΔGk+1,则k+1时刻的增益为

其中:
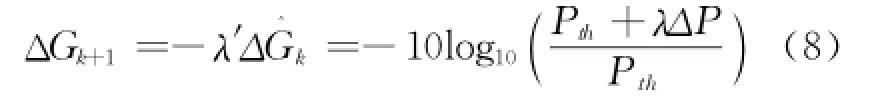
式中:λ′、λ为增益调节衰减因子,控制增益调节步进,避免信号变化较大时出现过冲调节,从而实现欠阻尼控制,同时可以抑制信号在门限附近时的振荡幅度。
通过式(8),可以在AGC控制过程中,根据回波信号功率自适应实时计算增益调节步进,达到快速和稳健的增益控制。
为避免信号在门限附近振荡,可选用双门限,将信号控制在一定的范围内。但信号起伏较大时,双门限会将信号进行矩形脉冲调制,信号在频谱分析时会出现多谱峰,影响雷达根据多普勒频率测量速度的性能。这种方法可应用在通信系统等对多普勒频率检测要求不高的系统。
2.3 AGC带宽控制
如果根据每次回波估计的信号幅度/功率即一步到位调节增益控制电压,则AGC带宽太大,会出现中频接收机输出信号不稳定,且影响AGC控制环路的稳定性。为有效控制AGC带宽,可以对每次输出的增益Gk进行α-β滤波。
输出的增益Gk进行α-β滤波分两个步骤,一步预测和一步更新:

其中:T为增益更新周期;Vk+1为k+1时刻增益更新速度,且有

式中:α、β为α-β滤波因子。
为降低算法复杂度,将Vk和β均设为零,通过仿真α=0.5性能最佳,此时α-β滤波器对应的3 dB带宽为114.7 Hz,如图4所示。
3 数字AGC设计仿真与分析
仿真中采用中频信号数字检波方法,均衡滤波采用32阶系数间隔1递减的滑动均衡滤波器,增益控制过程中增益调节衰减因子λ=0.25,α-β滤波器因子α=0.5,β=0。

图4 数字AGC环路滤波α-β滤波器幅频响应
仿真中,脉冲信号重频为1 k,每个脉冲为13位巴克码,子码宽度2 us,距离门宽度180 us,信号中频60 MHz。中频接收机归一化输出电平Pth=0 dB(0.632 V),雷达开机时设置AGC初始增益-20 dB。方案中,得到增益Gk+1后,查找AGC电压-增益曲线,再通过内插法得到较为精确的AGC电压输出值。
3.1 典型幅度变小阶跃信号数字AGC仿真
仿真中假设信号幅度从2 V阶跃变化到0.8 V,分别仿真信号叠加噪声和无噪声两种情况下的数字AGC性能。数字AGC控制后中频接收机输出的信号仿真结果,如图5所示。
从图5可以看出,信号幅度由大信号突然减小1.2 V时,数字AGC在15个重频内即可将接收机输出控制到归一化输出电平信号,而且在输出归一化信号时,归一化幅度起伏较小。


图5 信号(无噪声)幅度2 V阶跃变化至0.8 V时数字AGC输出仿真结果
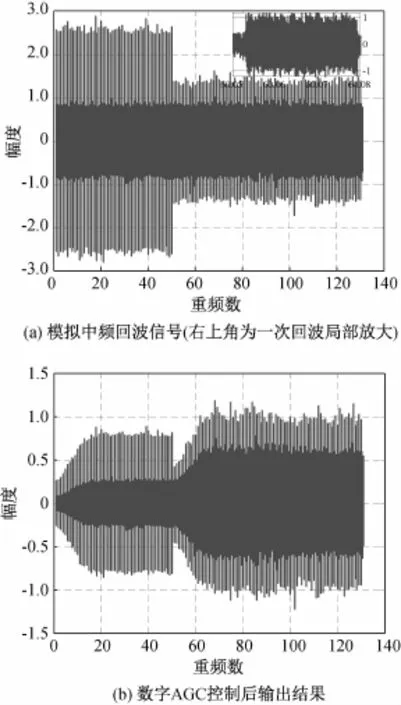
图6 信号(0.2 V噪声)幅度2 V阶跃变化至0.8 V时数字AGC输出仿真结果
图6为信号叠加均值为0 V,标准差为0.2 V的高斯随机噪声后的仿真结果,从图可看出数字AGC仍具有良好的性能。其中,图中(a)显示信号幅度为2.5 V,其实不是,因为图中每个重频都是一个脉冲,每个脉冲由13个子脉冲组成,里面有60 M的中频调制信号,此中频调制信号的幅度是均值为2 V,标准差为0.2 V的高斯信号。但缩小后,整体看,表现的是整个脉冲内中频信号幅度的最大值,接近2.5 V。同理,对图(b)也是表现出控制后的信号幅度大于门限电压0.632 V。另外,图(b)中右半部分得到的信号幅度比左半部分高,其实是相应噪声放大倍数大的原因造成。
3.2 典型幅度增大阶跃信号数字AGC仿真
仿真中假设信号幅度从0.8 V阶跃变化到2 V,信号无叠加噪声时通过数字AGC控制后中频接收机输出的信号仿真结果如下图所示。
从图7可以看出,信号幅度由小信号突然增大1.2 V时,数字AGC在7个重频内即可将接收机输出控制到归一化输出电平,而且没有出现输出信号阻尼振动的现象。

图7 信号(无噪声)幅度0.8 V阶跃变化至2 V时数字AGC输出仿真结果
4 结论
通过数字信号处理估计信号的功率/幅度并实时计算估计值与归一化输出电平的增益,然后调节增益衰减因子和α-β滤波器系数,可以实现自适应步进的欠阻尼稳健AGC和其带宽的控制。仿真结果可以看出,合适地选择衰减因子和α系数,可以使数字AGC兼具响应和收敛速度快、稳健性高的特点。
[1] 王彦,曹鹏,费元春.数字中频接收机的设计与实现[J].电讯技术,2004,44(5):41-44.
[2] 周顺,徐志军,杨田.数字中频接收机中的数字AGC的设计与实现[J].军事通信技术,2008,29(1):38-41.
[3] 童智勇,陈佳民,杨汝良.用于星载SAR数字AGC增益控制的双门限步进法[J].遥感技术与应用,2007,22(1):83-87.
[4] 金俊坤,吴嗣亮,孙武.某型伪码测距雷达的数字AGC设计[J].现代雷达,2005,27(10):75-78.
[5] 刘艳.基于FPGA的大动态范围数字AGC的实现[J].电子设计工程,2009,17(8):42-44.
[6] 常鸿,田龙,吴增印.一种用于接收微波的基带数字AGC设计[J].空间电子技术,2010,(4):47-49.
Adaptive Step Digital AGC Design and Simulation for Pulse Radar
ZHU Lu1, ZOU Bo2, JIANG Li-zhong2
(1.92941 forces 120th Research Institute,Huludao Liaoning,125001;2.Shanghai Radio Equipment Research Institute,Shanghai 200090,China)
It is an inevitable trend that digital design for analog AGC applicated on radar. Based on the study of digital design for analog AGC,an AGC control arithmetic for pulse radar with adaptive-step,adjustable AGC bandwidth and combination of speed and robustness is proposed on this paper.Simulation and analysis results indicate that the arithmatic has good performance and fast response ability.Besides,underdamped control can be implemented by adjusting the gain attenuation factor and AGC bandwidth control can be implemented by modificating the coefficient ofα-βfilter.
radar;analog;digital;adaptive step
TN958
A
1671-0576(2014)02-0022-06
2013-05-06
朱 璐(1981-),女,工程师,主要从事制导控制技术研究。

