基于互素对称阵的近场源定位
梁国龙 韩 博
基于互素对称阵的近场源定位
梁国龙 韩 博*
(哈尔滨工程大学水声技术重点实验室 哈尔滨 150001)
针对近场源定位中存在的孔径损失问题,该文提出了一种新的近场源定位算法。该算法采用互素对称阵列,使得阵元间距不必限制于1/4信号波长。首先构造一个特殊的四阶累积量矩阵,进而采用MUSIC算法估计信源方位角,然后在每个估计方向上搜索距离。该算法将近场源2维定位问题转化为多次1维搜索,且参数自动配对。互素对称阵的使用有效地扩展了阵列孔径,提高了空间分辨概率和参数估计性能。计算机仿真验证了该算法的有效性。
信号处理;源定位;近场;阵列处理;互素对称阵;累积量
1 引言
阵列孔径是影响信源方位角分辨率和定位精度的重要因素之一。在阵元数目有限的情况下,稀疏布阵可以增加阵列孔径,为避免稀疏阵列带来的空间模糊问题,文献[14-16]给出了稀疏阵列的设计方法及其在远场条件下的应用。本文根据近场条件,将互素阵[15]扩展,采用互素对称阵模型,提出一种新的近场源定位算法。首先构造了一个特殊的四阶累积量矩阵,利用MUSIC算法估计信源方向角。然后根据方位角估计值搜索信源距离参数。该算法将2维搜索问题转化为多次1维搜索,无需参数配对,采用互素对称阵提高了DOA空间分辨概率和定位性能。
2 信号模型
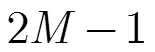
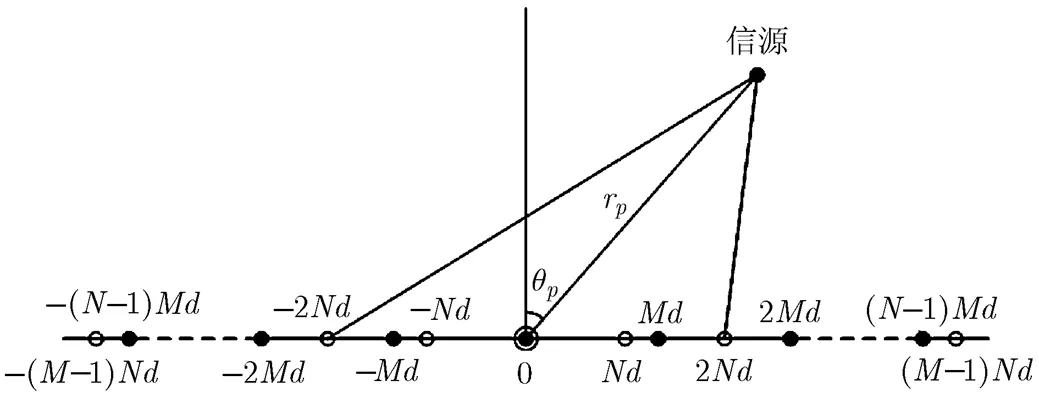
图1 阵列几何模型
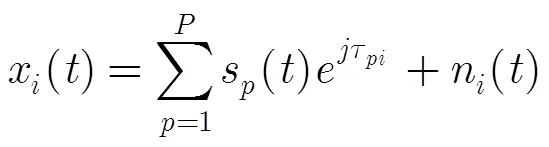
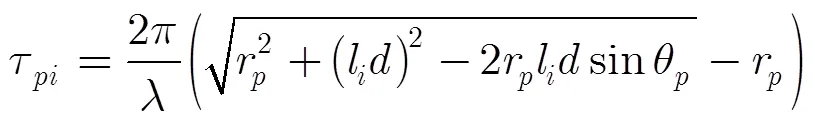
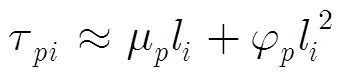
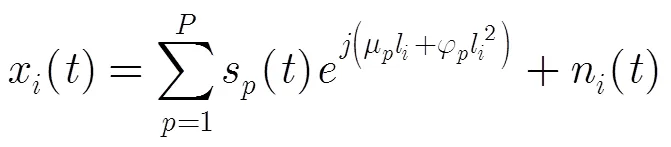
阵列接收信号表示为
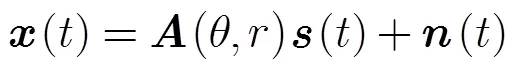
式中
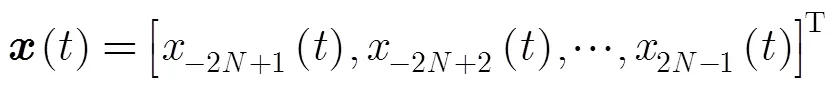
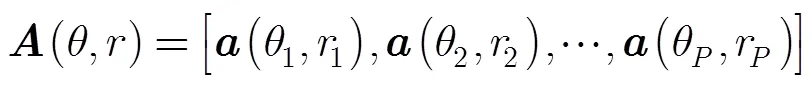
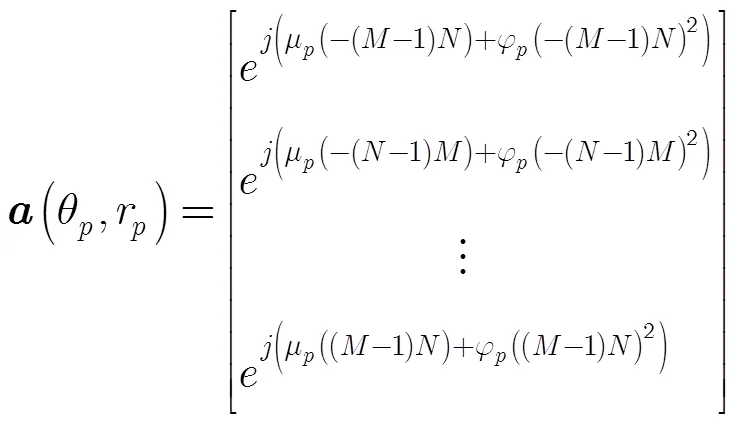
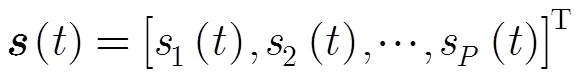
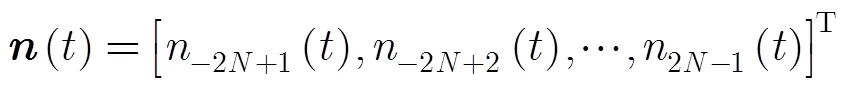
不失一般性,本文做如下假设:
(1)信号为零均值、非高斯的窄带平稳随机过程,且具有非零峰度,信号之间互不相关;
(2)各阵元接收的噪声为零均值的高斯白噪声,并与信号相互独立;
3 基于互素对称阵的混合阶MUSIC算法
3.1 构造累积量矩阵
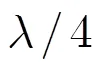
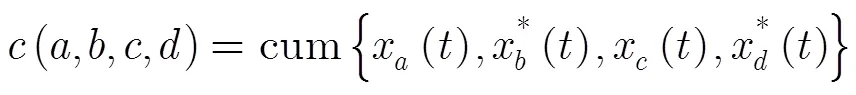
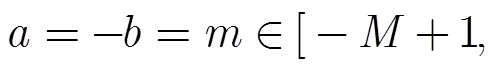
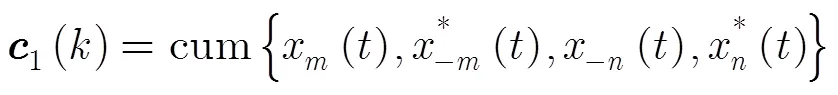

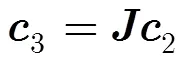
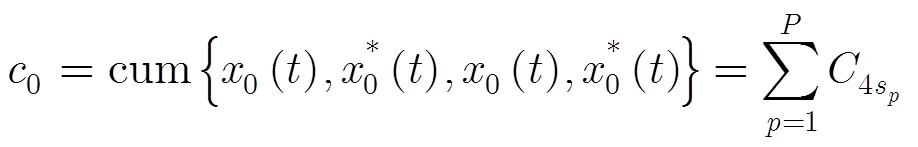
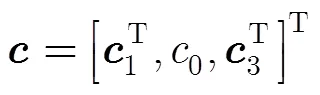
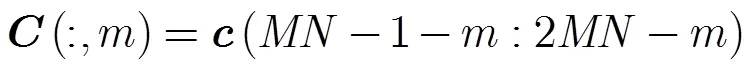
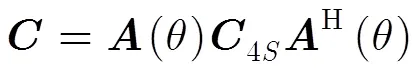
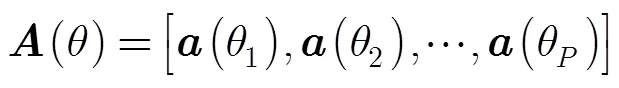
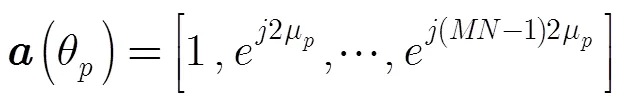
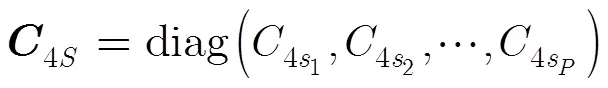
3.2 近场源DOA估计
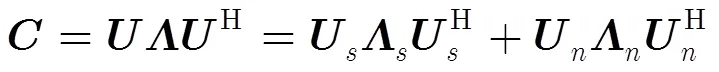
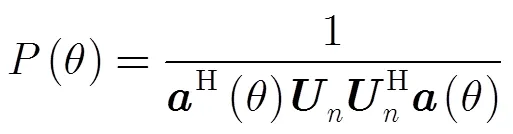
3.3 近场源距离估计
阵列数据协方差矩阵如下:
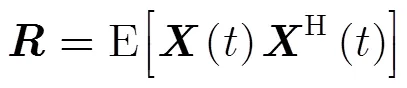
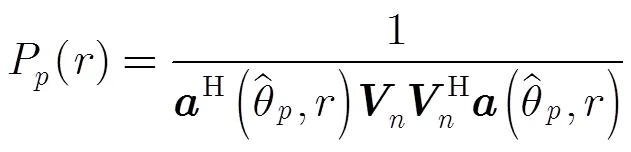
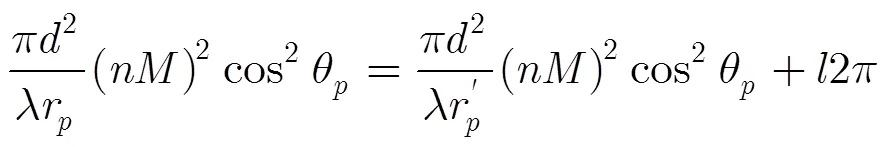
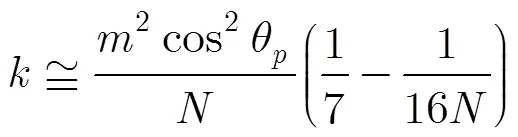
那么,式(29)右边部分需满足:
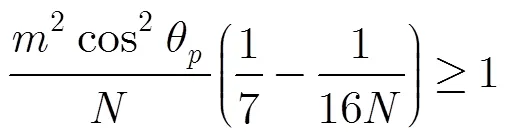

3.4 计算量分析
4 计算机仿真
4.1 DOA分辨概率仿真
从图2和图3可以看出,本文算法成功分辨两个目标的概率比文献[12]和文献[13]中算法的分辨概率高。这是因为该算法采用了互素对称阵列,在阵元数目相同的条件下,有效扩展了阵列孔径。
4.2 参数估计性能仿真
5 结束语
本文以互素对称阵为阵型依托,提出了一种近场源定位算法。该算法通过合理选择不同阵元数据,构造一个特殊的四阶累积量矩阵,使得该矩阵仅与信源方位角有关;进而利用MUSIC算法进行方位角估计,然后在每个方位角估计值方向上搜索信源距离参数。互素对称阵的采用,使得在阵元数一定的条件下,大大扩展了阵列孔径。仿真结果表明,本文算法提高了信源DOA分辨概率和定位精度。
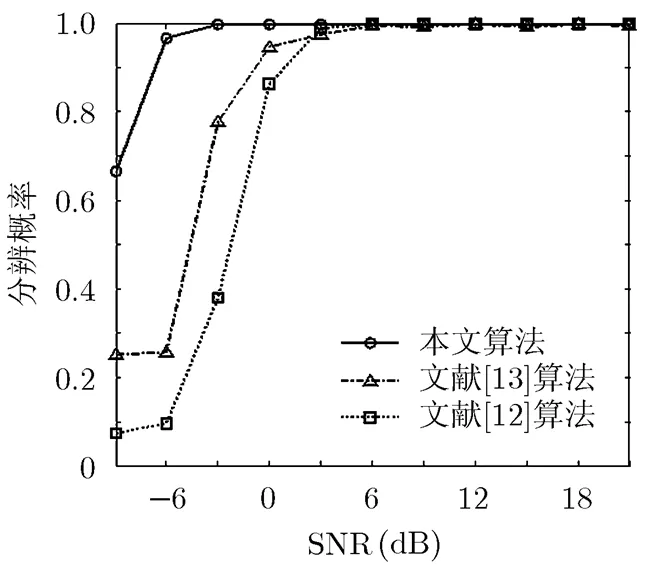
图2 分辨概率随信噪比变化情况
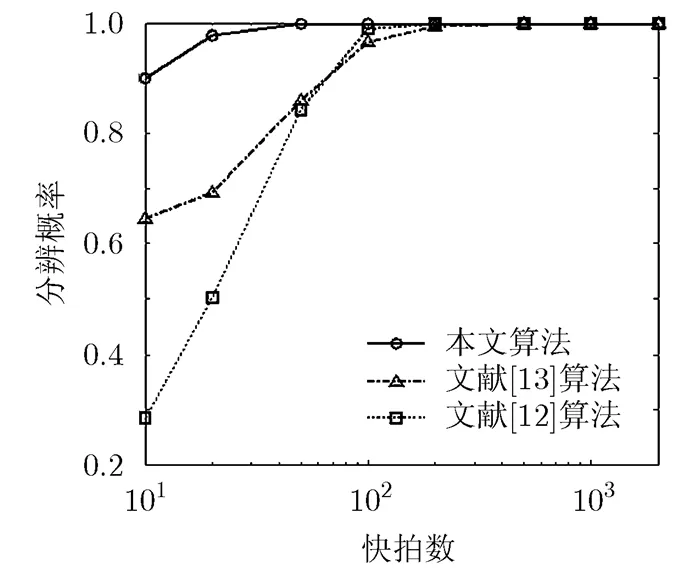
图3 分辨概率随快拍数变化情况
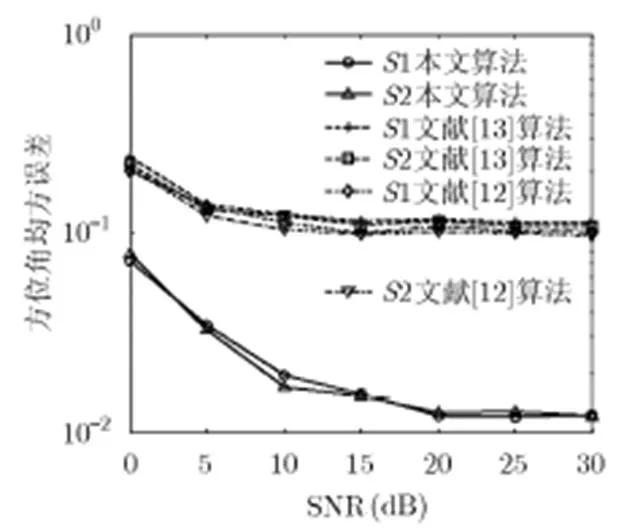
图4 方位角均方误差随信噪比变化情况
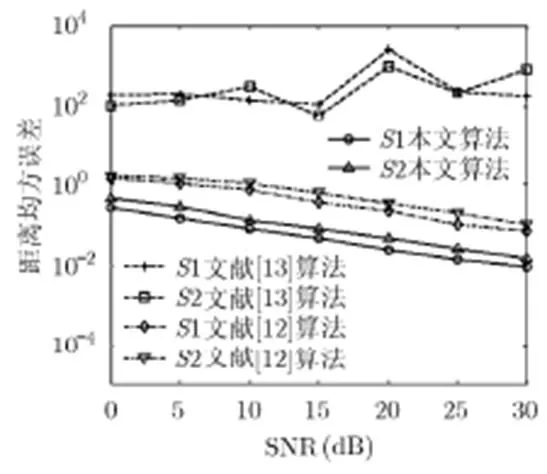
图5 距离均方误差随信噪比变化情况
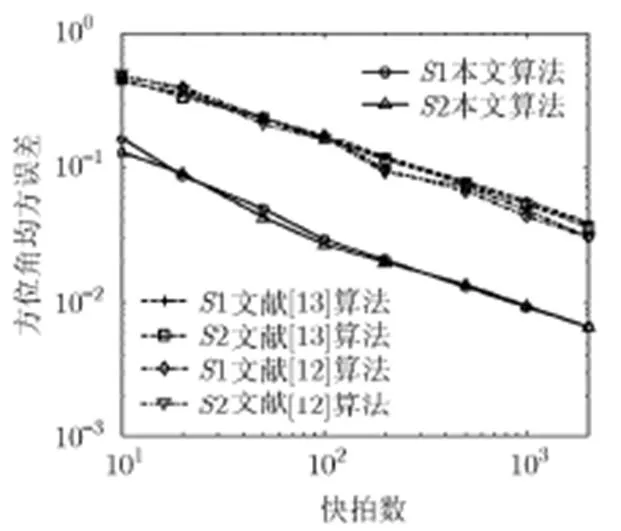
图6 方位角均方误差随快拍数变化情况
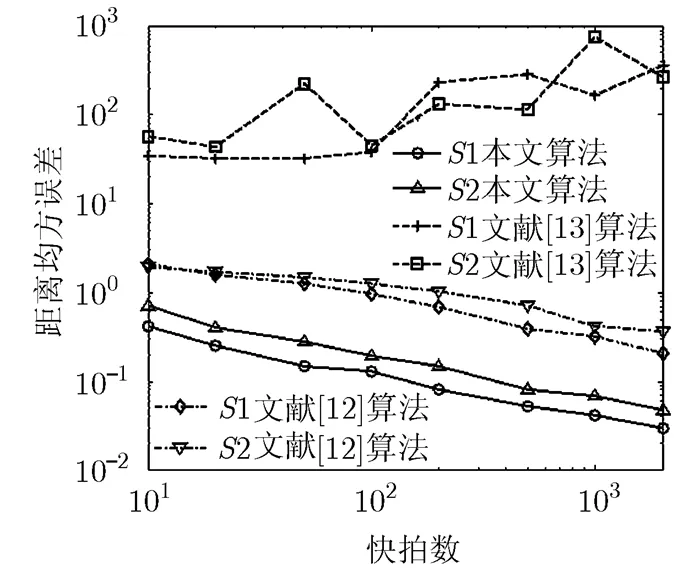
图7 距离均方误差随快拍数变化情况
[1] McCloud M L and Scharf L L. A new subspace identification algorithm for high-resolution DOA estimation[J]., 2002, 50(10): 1382-1390.
[2] 李鹏飞, 钟子发, 张旻. 未知信源数目的DOA估计方法[J]. 电子与信息学报, 2012, 34(3): 576-581.
Li Peng-fei, Zhong Zi-fa, and Zhang Min. Direction of arrival estimation methods without sources number[J].&, 2012, 34(3): 576-581.
[3] Hu N, Ye Z F, Xu X,.. DOA estimation for sparse array via sparse signal reconstruction[J]., 2013, 49(2): 760-773.
[4] Huang Y D and Barkat M. Near-field mutiple sources localization by passive sensor array[J]., 1991, 39(7): 968-975.
[5] Yuen N and Friedlander B. Performance analysis of higher order ESPRIT for localization of near-field sources[J]., 1998, 46(3): 709-719.
[6] 陈建峰, 张贤达, 吴云韬. 近场源距离、频率及到达角联合估计算法[J]. 电子学报,2004, 32(5): 803-806.
Chen Jian-feng, Zhang Xian-da, and Wu Yun-tao. An algorithm for jointly estimating range, DOA and frequency of near field source[J]., 2004, 32(5): 803-806.
[7] 徐元欣, 王安国, 聂仲尔. 基于四阶累积量的近远场源多参数联合估计算法[J]. 电子与信息学报, 2011, 33(6): 1379-1384.
Xu Yuan-xin, Wang An-guo, and Nie Zhong-er. Joint multi- parameters estimation of near-field and far-field sources based on the fourth order cumulant[J].&, 2011, 33(6): 1379-1384.
[8] 王波, 王树勋. 一种基于二阶统计量的近场源三维参数估计方法[J]. 电子与信息学报, 2006, 28(1): 45-49.
Wang Bo and Wang Shu-xun. A three-dimensional parameter estimation method of near field sources based on second statistics[J].&, 2006, 28(1): 45-49.
[9] Zhi W and Chia M Y. Near-field source localization via symmetric subarrays[J]., 2007, 14(6): 409-412.
[10] 刘亮, 陶建武, 黄家才. 基于稀疏对称阵列的近场源定位[J]. 电子学报, 2009, 37(6): 1307-1312.
Liu Liang, Tao Jian-wu, and Huang Jia-cai. Near-field source localization based on sparse symmetric array[J]., 2009, 37(6): 1307-1312.
[11] 蒋佳佳, 段发阶, 陈劲, 等. 一种近场和远场混合信号源的分类和定位算法[J]. 华中科技大学学报(自然科学版), 2013, 41(4): 46-50.
Jiang Jia-jia, Duan Fa-jie, Chen Jin,.. Algorithm to classify and locate near-field and far-field mixed sources[J].(), 2013, 41(4): 46-50.
[12] He J, Swamy M N, and Ahmad M O. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J]., 2012, 60(4): 2066-2070.
[13] Liang J and Liu D. Passive localization of near-field sources using cumulant[J]., 2009, 9(8): 953-960.
[14] Pal P and Vaidyanathan P P. Nested arrays: a novel approach to array processing with enhanced degrees of freedom[J]., 2010, 58(8): 4167-4181.
[15] Vaidyanathan P P and Pal P. Sparse sensing with co-prime samplers and arrays[J]., 2011, 59(2): 573-586.
[16] Pal P and Vaidyanathan P P. Multiple level nested array: an efficient geometry for 2th order cumulant based array processing[J]., 2012, 60(3): 1253-1269.
梁国龙: 男,1964年生,教授,研究方向为水声定位与导航、水声对抗、水声目标探测等.
韩 博: 男,1986年生,博士生,研究方向为阵列信号处理、水下定位与导航等.
Near-field Sources Localization Based on Co-prime Symmetric Array
Liang Guo-long Han Bo
(,,150001,)
For the issue of aperture loss appears when localizing near-field sources, a novel near-field source localization algorithm is presented. The algorithm is based on the co-prime symmetric array, thus the intersensor spacing need not be limited to quarter-wavelength. First, a special fourth-order cumulant matrix is constructed to estimate the azimuth angles of sources by the MUSIC algorithm. Second, the range parameters of sources can be obtained by searching the spectral peak with each estimated bearing angle. The algorithm transforms the two-dimensional localization issue into several one-dimensional searching issue, and the parameters are automatically paired. The array aperture is extended by using co-prime symmetric, and the algorithm improves the spatial resolution and parameters estimated performance. Simulation results verify the effectiveness of the proposed algorithm.
Signal processing; Sources localization; Near-field; Array processing; Co-prime symmetric array; Cumulant
TB566
A
1009-5896(2014)01-0135-05
10.3724/SP.J.1146.2013.00756
2013-05-27收到,2013-10-25改回
国家自然科学基金(51279043, 51209059),水声技术国家级重点实验室基金(9140C200203110C2003)和黑龙江省普通高等学校青年学术骨干支持计划(1253G019)资助课题
韩博 hanbo710@126.com

