机载相控阵波束指向校正*

任燕飞

(西南电子技术研究所，四川 成都610036)

0 引言

相控阵天线通过电扫描的方式，可以快速实现阵列波束指向调整。相对于传统定向天线，无需机械伺服系统，设计更为简单。同时，由于天线采用多个阵元，可以产生阵列增益，从而有效提高天线的G/T值。这些优势，使得相控阵天线广泛应用到了雷达、通信、声呐、射电天文等领域［1－3］。在航空电子设备中，机载卫星通信也可以采用相控阵天线。通常的相控阵卫星通信天线安装在飞机机背位置，卫星的角度信息通过飞机飞控系统的姿态测量系统和航向测量系统，可以准确计算出来［4］。但在某些特殊情况下，卫星通信天线可能会安装在飞机机翼上，此时，由于飞机机翼在飞行过程中会出现变形，机翼和机身不在是一个刚体结构。飞机飞控系统提供的卫星角度信息由于机翼的变形，已经不再准确，所以，必须采用角度校正手段，克服这种变形造成的波束指向误差，才能保证相控阵天线的正常工作。

1 问题模型描述

1.1 相控阵天线原理

相控阵天线通常分为两大类，一是模拟相控阵，二是数字相控阵。模拟相控阵的相位调整和信号合成通过模拟射频器件构成，而数字相控阵通常在中频或者基带进行数字化，并在数字域实现相位调整和信号合成［5］。但无论采用何种方式，相控阵的基本原理是相同的，都是根据波束指向的角度信息，获得相位调整权矢量，从而实现相控阵的波束合成。

假设阵列由M×N个均匀平面阵列构成，阵元间距为半个波长。如果坐标原点接收信号为s(t)ejωt，则第(m，n)个阵元接收信号可以表示为

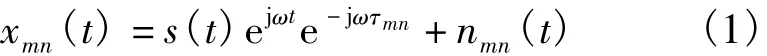
式中，s(t)表示信号复基带，而信号相对于原点延时为τmn，则是阵元接收噪声信号nmn(t)，服从均匀高斯分布，m=1，2，…，M，n=1，2，…，N。根据平面阵列几何关系，不难确定

式中，矢量k为入射信号波数矢量，与信号波束指向为方位角φ，俯仰角θ有关，该角度又称为信号波达方向DOA，kT表示矢量k的转置，pmn为阵元(m，n)的坐标矢量，即

式中，pxmn，pymn，pzmn分别为矢量pmn在 x 轴，y 轴和 z轴投影值，d为相邻阵元的间距。由于阵列为均匀平面阵，因此阵元间距相等，且矢量pmn在z轴投影值为0。

相控阵通过对每个接收信号进行复数加权，从而调整信号的相位，使得所有阵元接收信号的相位对齐，然后合成输出

式中，“H”表示取权矢量w的共轭转置，x(t)为接收信号的矢量表示。虽然阵列是均匀平面阵，但权矢量w和信号矢量x(t)均为MN维列矢量。理论上，相控阵天线权矢量为

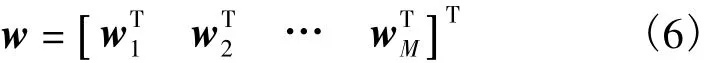
式中，wm表示第m行阵元对应的权矢量，即

而第(m，n)个阵元对应的权值为

可见，根据式(2)～式(4)，该权值决定于信号相对于阵面的信号波达方向(DOA，Direction of Arrival)。

1.2 系统坐标设计

为了说明相控阵天线波束指向角度描述方法，定义三个坐标系统。一个是以地球为参考的坐标系XYZ。该坐标系的XY平面与水平面平行，X轴为纬度方向，指向北方，Y轴方向为经度方向，指向东方，Z轴为垂直水平面方向，指向天空。第二个坐标系为飞机机身坐标系X'Y'Z'，X'Y'平面为飞机机身平面，X'指向机头方向，Y＇指向右侧机翼，Z'垂直机身平面指向天空。第三个坐标系统就是安装在机翼上的相控阵阵面自身定义坐标系X″Y″Z″，该坐标系的X″Y″平面为阵面平面，Z″垂直该平面指向天空。坐标系俯视图如图1所示。

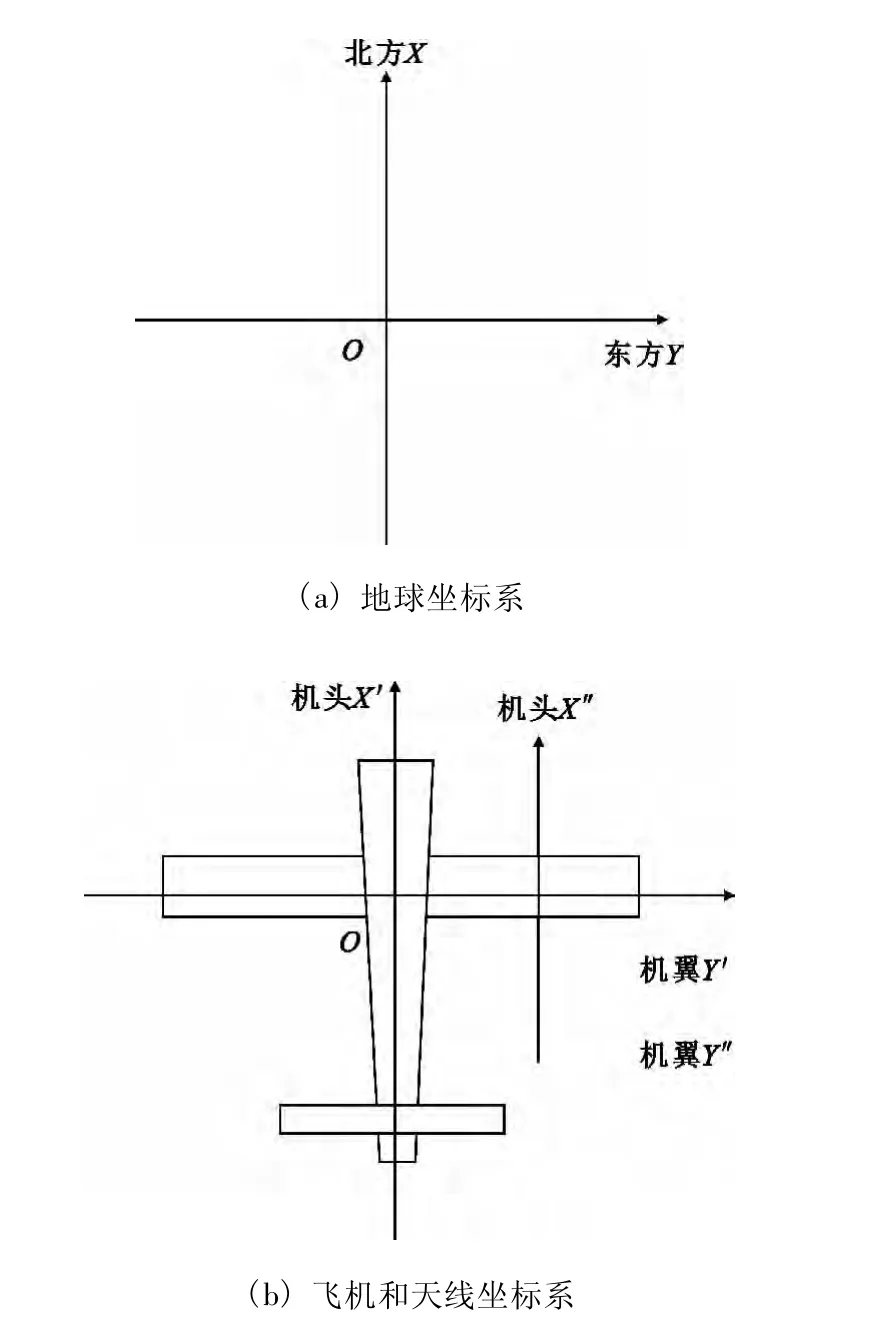
图1 三种坐标系Fig.1 Three types of coordinate system

安装在飞机上的航空电子系统，一个重要功能就是对飞机位置、姿态进行测量［6］。位置参数包括了飞机的经纬度、高度，姿态参数则包括了航向角α、俯仰角β和横滚角γ。通过位置参数和姿态参数，如果卫星位置是已知的，则可以计算出卫星信号相对于飞机的角度(θ，φ)，即DOA。但是，由于姿态参数是相对于地球坐标系XYZ，而DOA又是相对于机身坐标系X'Y'Z'，所以，这个DOA信息对于安装在机翼上的相控阵天线而言是不正确的。

由于相控阵只关心信号入射角度，而坐标原点移动并不会改变信号角度，所以可以假设上述三个坐标系的原点始终是重合的。飞机在飞行过程中，随着航向和姿态不同，上述两个坐标系的相对关系会发生变化。这些坐标变换关系，称为相控阵天线波束指向角度校正的理论依据。

2 指向角度校正方法

2.1 校正目的

由于机翼在飞行过程中的变形，安装在机翼上的相控阵天线阵面坐标与机身坐标是不重合的。航电系统能够提供卫星相对于机身坐标系的DOA参数(θ，φ)，也能提供飞机机身相对于地球坐标系的姿态参数(α，β，γ)。角度校正的目的，就是利用航电系统提供的上述参数，计算卫星相对于阵列坐标系的DOA参数。

2.2 校正方法

校正方面的基本思想是通过航电系统提供的姿态参数和卫星DOA参数，计算卫星在地球坐标系下的坐标。然后利用相控阵自身安装的电子罗盘，测量相控阵天线阵面的姿态参数。结合上述两方面数据，计算卫星相对于阵面的DOA数据。

2.2.1 卫星位置计算

根据前文描述，假设三个坐标系的原点是重合的，而且，航电系统提供已知参数包括了(θ，φ)和(α，β，γ)。根据这些参数，我们首先计算卫星位于地球坐标系中的坐标。虽然卫星坐标数据在航电系统中是已知的，但考虑到相控阵波束指向校正模块与航电系统接口的兼容性，把姿态数据和DOA数据作为已知条件更具有可行性。

根据坐标定义，卫星在机身坐标系中坐标为

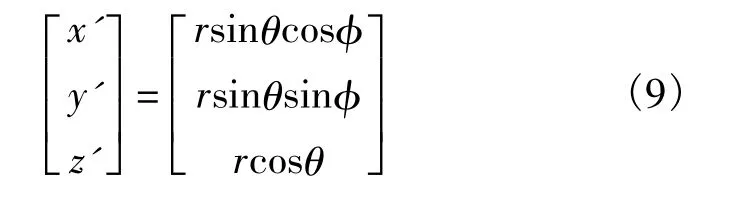
同时，根据坐标变换关系和姿态参数的定义，可以获得坐标变换矩阵 R［7］:

式中，

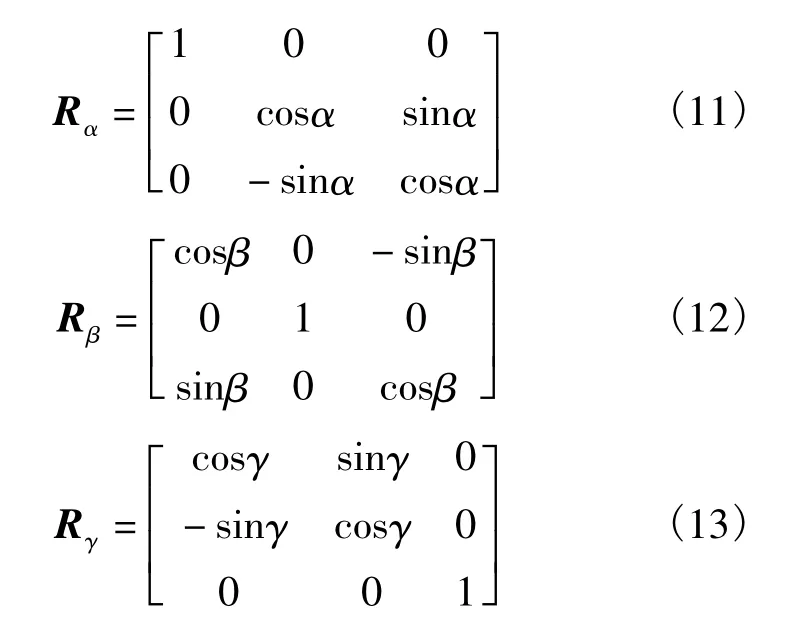
由坐标变换矩阵和机身坐标系下坐标，可以计算卫星在地球坐标系下坐标:

2.2.2 阵面姿态测量

相控阵天线安装在机翼上，机翼变形使得相控阵阵面姿态与航电系统飞机姿态不同。为了获得卫星相对于阵面的角度，必须获得相控阵阵面姿态信息，即阵面的航向角δ、俯仰角η和横滚角μ。有两种方面可以解决该问题，一是通过机翼的应力变形进行测量［8］，二是通过安装在阵面上的电子罗盘进行测量。

如果采用应力测量的方法，需要安装光纤传感器，但该测量方法的精度难以保证。由于微机电系统(MEMS，Micro－electromechanical System)技术的发展，电子罗盘的体积和精度得到了很大提高，相对于光纤传感器具有更好的精度。

电子罗盘通常包括两个功能部分，一是航向角测量，二是姿态角测量［9］。磁阻传感器和陀螺仪是构成电子罗盘的主要部件。体积和测量精度是影响相控阵波束指向校正的主要因素。同时，相应速度、功耗、接口、安装、环境适应性也是设计中需要考虑的问题。

无论如何选择电子罗盘，其输出参数是以阵面为被测面，输出参数包括航向角δ、俯仰角η和横滚角μ。

2.2.3 校正角度计算

把卫星在地球坐标系下的坐标转换到阵面坐标系，需要利用电子罗盘的测量参数。定义坐标转换矩阵

式中，

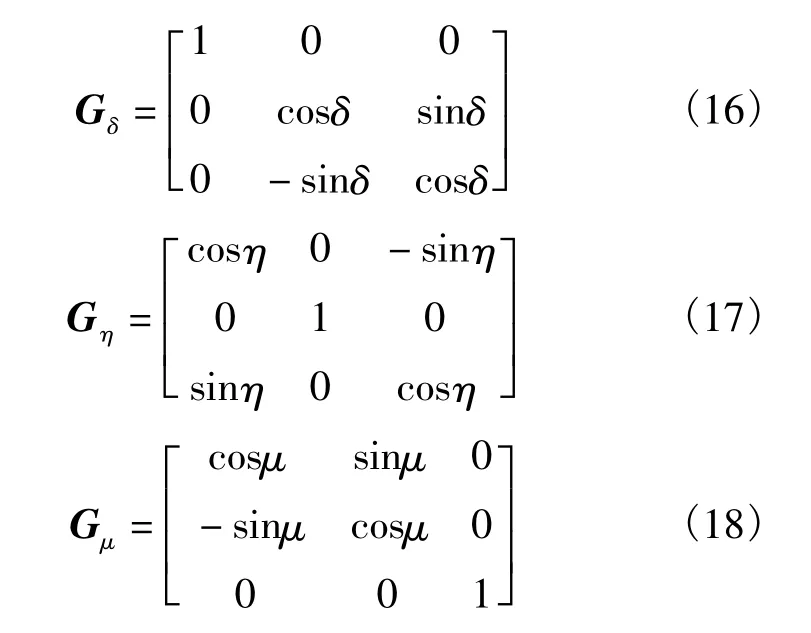
同样根据坐标变换关系，并考虑式(14)～式(18)，卫星在阵面坐标系下的坐标为

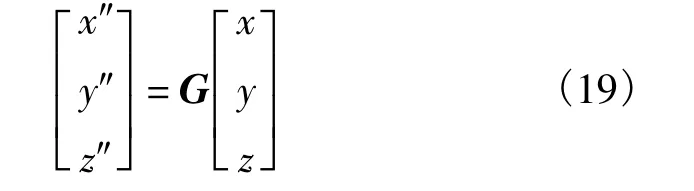
而阵面坐标系下的波束指向角度(θ″，φ″)同卫星坐标满足如下关系式

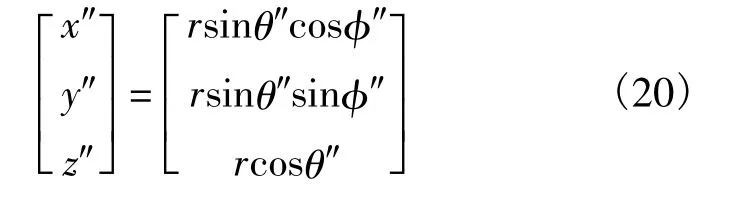
求解上述方程，即可得到(θ″，φ″)。

3 计算机仿真

3.1 校正方向图

仿真假设阵列为8×8均匀平面阵，阵元间距为半个波长。假设入射角对于阵面的俯仰角为30°，方位角为60°时，随机设置航电系统提供的卫星信号DOA参数，并仿真阵列方向图。根据相控阵天线原理，阵列方向图可以定义为

而权矢量按照式(8)计算。在不进行角度校正情况下，阵列方向图如图2所示，图2(a)和图2(b)分别为三维图和投影图。从图2看出，此时阵列不仅主瓣无法指向卫星，而且出现很大栅瓣。而图3为进行校正后的方向图，阵列主瓣指向了期望的角度，而且没有栅瓣出现，与相控阵天线的理论方向图一致。

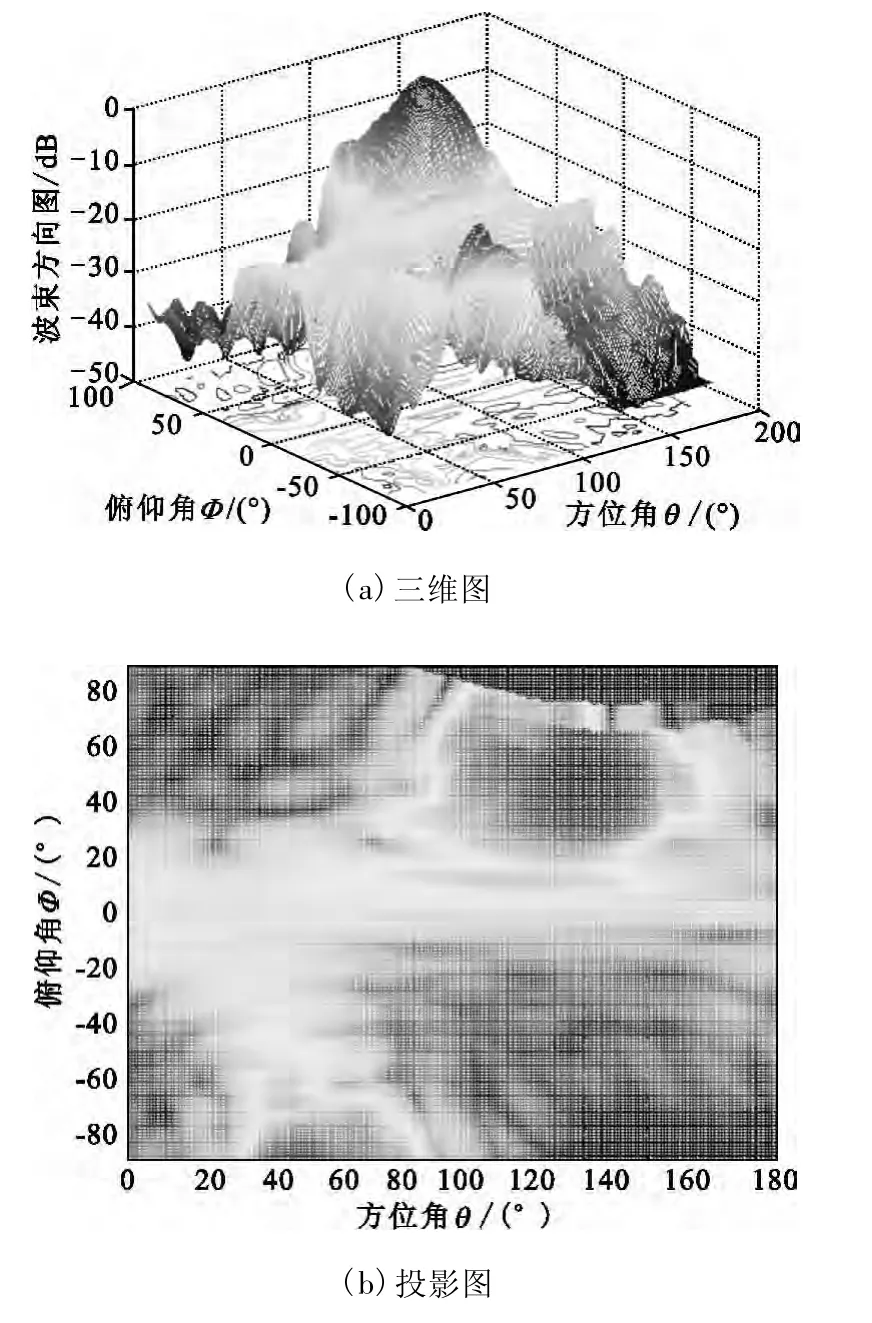
图2 无校正时的阵列方向Fig.2 Array pattern without calibration

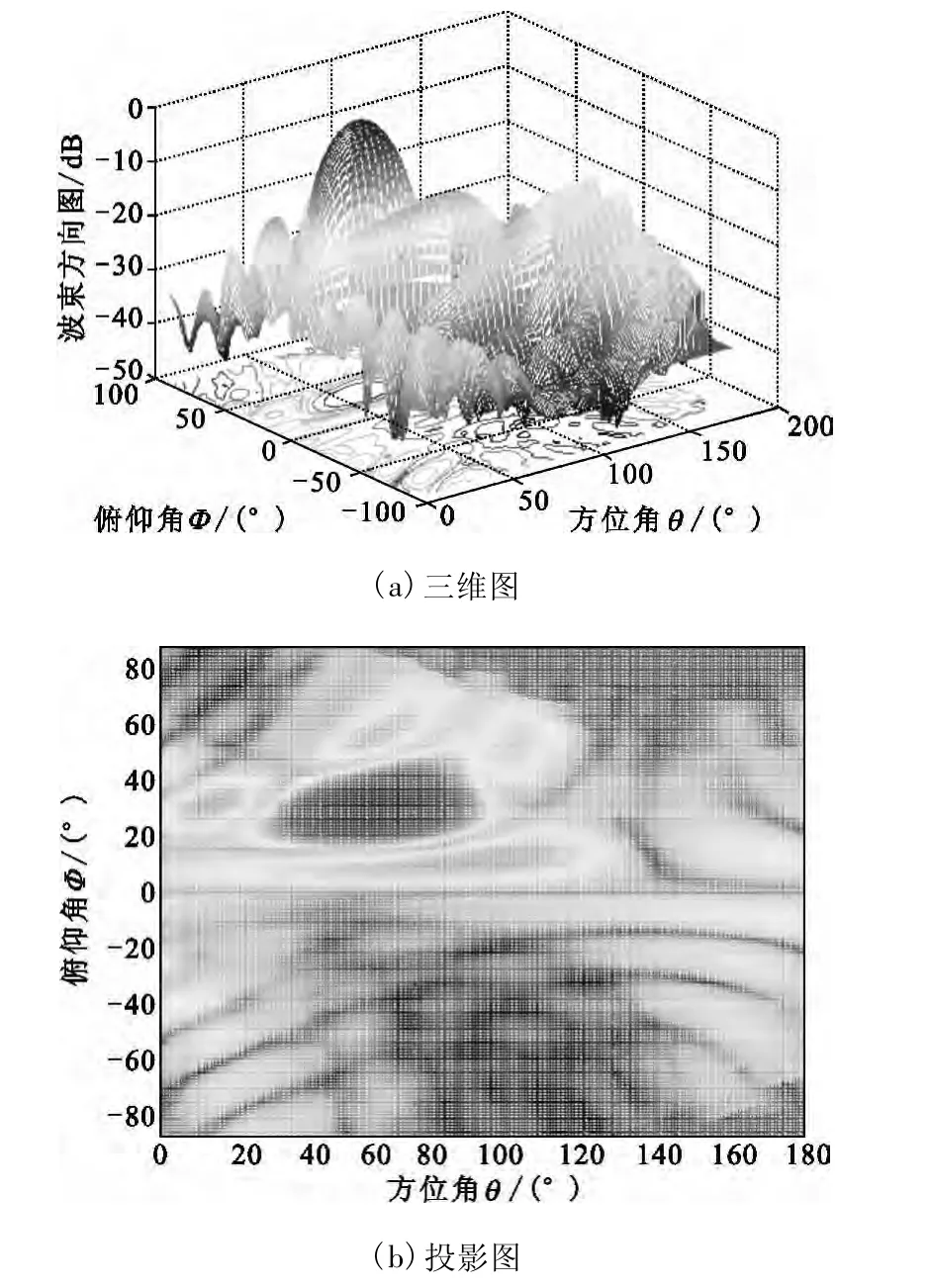
图3 有校正时的阵列方向Fig.3 Array pattern with calibration

3.2 测量误差影响

同样采用8×8均匀平面阵，若电子罗盘测量的航向角、俯仰角、方位角均存在误差，且均服从N(0，σ2)的高斯分布。若角度测量的误差方差σ2分别为0、4、8、16，对其进行仿真，观察相控阵输出信噪比SNRout，结果如图4所示。从图4中可见，当输入信噪比SNRin一定时，姿态参数测量误差导致了相控阵阵列增益下降，且随着误差σ2的增大，下降越严重。

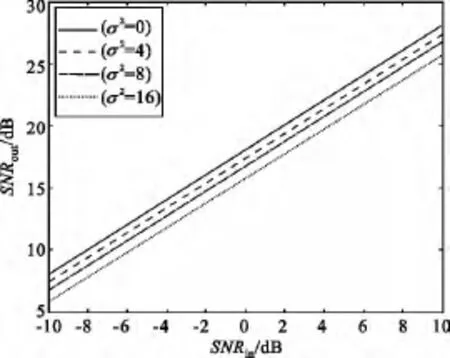
图4 姿态参数误差影响Fig.4 Error effect of attitude parameters

4 结语

国内外学者对相控阵天线的校准研究非常多，但主要集中在相控阵天线通道不一致上，而对于平台形变引起的波束指向偏差研究很少。通过电子罗盘和坐标变换，可以解决机翼变形对相控阵天线波束指向角度校正的问题。这种方法适用于任何可变形平台上的天线波束指向校正。由于校正的性能同测量因素相关，提高电子罗盘的测量精度是未来工作。

［1］WARNICK K F，IVASHINA M V，WIJNHOLDS S J，et al.Polarimetry with Phased Array Antennas:Theoretical Framework and Definitions［J］.IEEE Transactions on Antennas and Propagation，2012，60(01):184 －196.

［2］VAN A A，BREGMAN J D，VAN CAPPELLEN W A，et al.Extending the Field of View with Phased Aray Techniques:Results of European SKA Research［J］.Proceedings of the IEEE，2009，97(08):1531－1542.

［3］KANT G W，PATEL P D，WIJNHOLDS S J，et al.EMBRACE:a Multi－beam 20，000－element Radio Astronomical Phased Array Antenna Demonstrator［J］.IEEE Transactions on Antennas and Propagation，2011，59(06):1990－2003.

［4］王志军，白旭平，刘琼俐，等.卫星通信系统中的抗干扰技术研究［J］.通信技术，2012，07(45):10－13.WANG Zhi－jun etc.Study on Anti－ interference Technology for Satellite Communication System［J］.Communications Technology，2012，07(45):10 －13.

［5］MANTEGHI M，BLANCO R A.Novel Technique for a Low － cost Digital Phased Array Design［J］.IEEE Transactions on Antennas and Propagation，2013，61(07):3495－3501.

［6］WU Z，YAO M，MA H，et al.Improving Accuracy of the Vehicle Attitude Estimation for Low－cost INS/GPS Integration Aided by the GPS － measured Course Angle［J］.IEEE Transactions on Intelligent Transportation Systems，2013，14(02):553－564.

［7］张伟，张安堂，肖宇.基于坐标旋转数字计算方法的三维坐标变换［J］.探测与控制学报，2011，33(02):73－80.ZHANG Wei，ZHANG An － tang，XIAO Yu.CORDIC Based Three － dimensional Coordinate Transform［J］.Journal of Detection ＆ Control，2011，33(2):73－80.

［8］李乃吉，王惠文，杨扬.连续分布式光纤传感器在测量大型构件形变中的应用［J］.仪器仪表学报，1992，13(02):214－219.LI Nai－ji;WANG Hui－wen;YANG Yang.Application of Continuous Distributed Optical Fiber Sensor in the Measurement of Large Strain［J］.Chinese Journal of Scientific Instrument，1992，13(2):214 －219

［9］张韦，刘诗斌，冯文光.基于磁通门的三轴电子罗盘自动误差补偿方法［J］.传感技术学报，2012，25(12):1692－1695.ZHANG Wei;LIU Shi－bin;FENG Wen－guang.Automatic Error Compensation Method of Three－Axis Electronic Compass Based on the Fluxgate［J］.Chinese Journal of Sensors and Actuators，2012，25(12):1692 －1695