SAVSTMV波束形成算法研究

卢中新，周胜增，高 源

(上海船舶电子设备研究所，上海 201108)

0 引 言

信号源方位(Direction of Arrival, DOA)估计方法主要包括常规算法和高分辨算法。常规波束形成的缺点是方位分辨力有限且抗干扰性能差；最小方差无畸变波束形成方法、多重信号分类(MUltiple SIgnal Classification, MUSIC)、导向最小方差(STeered Minimum Variance, STMV)波束形成等高分辨算法方位分辨力高，波束宽度不受瑞利限限制，但阵元域处理存在计算量大和稳健性差等缺点。文献[1]提出了基于子带子阵的自适应波束形成算法，该算法具有计算量小、稳健性好、分辨力高等特点。

矢量水听器可以同时测量声场中的声压信息和振速信息，因此，相比于常规声压阵，矢量阵可获得更多的信息，波束形成优于声压阵。文献[2]将 STMV算法应用到矢量阵中，提出了矢量阵导向最小方差(VSTMV)波束形成算法。为了改善VSTMV波束形成算法稳健性并减小其计算量，本文将子阵域STMV应用与矢量阵相结合，提出了子阵域 VSTMV波束形成算法(SAVSTMV)，进行了理论和仿真研究，并与矢量阵常规波束形成进行了对比。

1 矢量水听器阵列信号模型[3,4]

假设M个二维矢量水听器(它们能同时测量声场中声压和质点振速的两个水平分量)组成均匀直线阵，间距为d，如图1所示。

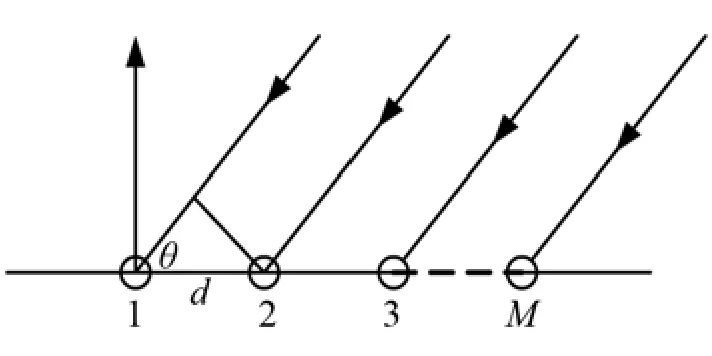
图1 等间距直线阵Fig.1 Uniform linear array

由图1可见，该阵型声压阵方向向量为：

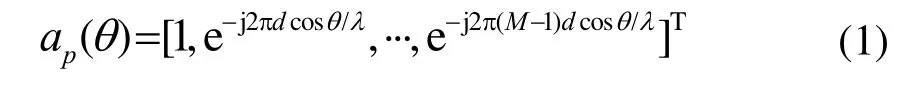
二维矢量传感器的方向向量为

则该阵型矢量阵方向向量为

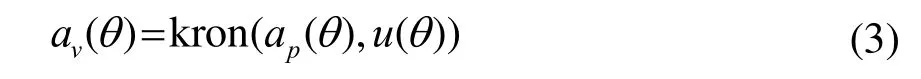
考虑J个信号源入射到矢量阵上，则第m个阵元接收的信号表示为

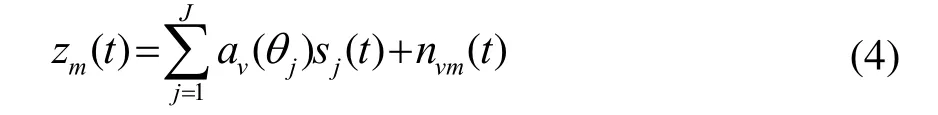
式中：θj表示第j个信号源的入射方向；sj(t)表示第j个信号源波形，是第m个阵元的声压和振速接收到的噪声矢量，

整个矢量阵接收信号可以表示为

分别表示S(t)、Nv(t)的傅里叶变换，fk∈ [fl,fh]，[fl,fh] 为信号分析频带，k=l,l+1,··,h为相应的频率下标。

2 VSTMV算法[2]

导向最小方差(STeered Minimum Variance,STMV)波束形成算法应用到矢量阵上简称为VSTMV，文献[2]中对此有详细的介绍，现将主要推导公式列出。矢量阵列频域输出向量表示为

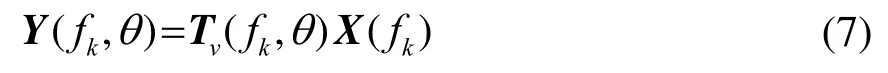
其中：

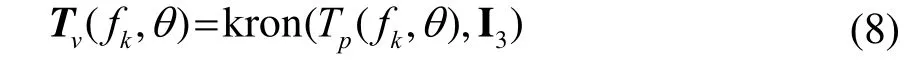
Tp(fk,θ) = diag(ap(θ))， I3为3阶单位阵。定义

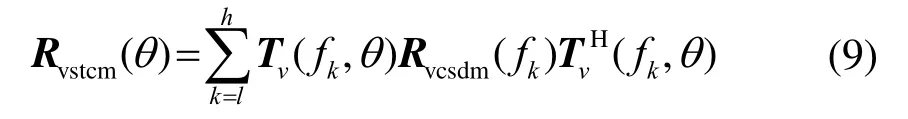
为矢量阵对应方向θ的导向协方差矩阵(Vector STeered Covariance Matrix, VSTCM)。其中

为频域数据协方差矩阵，那么矢量阵权向量为

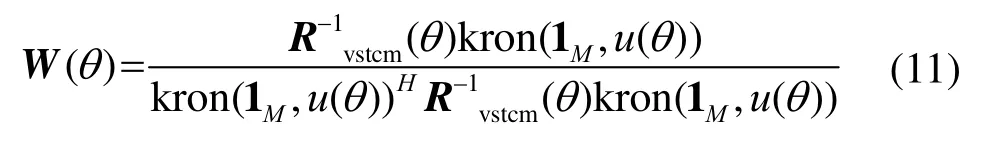
其中，1M表示为M×1维单位向量，则VSTMV波束形成的频域波束输出为

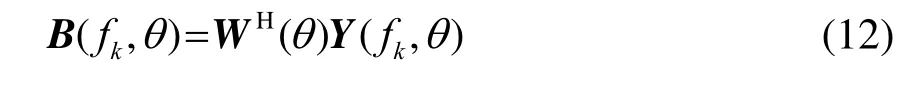
3 SAVSTMV波束形成算法

自适应波束形成算法中随着阵元数目的增加，阵列数据协方差矩阵的维数也随着增大，从而矩阵求逆计算量剧增，可以通过划分子阵来降低矩阵维数，减少矩阵求逆计算量。子阵处理基本原理是将整个接收阵划分成若干个子阵，对每个子阵进行常规波束形成，然后将预成在相同方向的不同子阵作为单个接收基元，最后对这些“子阵基元”进行自适应波束形成[1]。

对于M元二维矢量水听器阵列，假设将其划分成N个子阵，每个子阵含有Na个阵元，则每个子阵中含有 3Na路信号(一个声压和水平方向两个振速信号)，对每个子阵进行矢量阵常规波束形成，同一预成方位下共形成N个子波束输出，最后将这N个子波束输出作为接收基元进行自适应波束形成。

定义矢量阵信号选择向量：

其中 INa为Na×1维单位向量。

重写式(7)，为

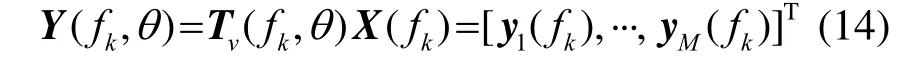
ym(fk)表示第m个阵元信号经过相移后的值，m= 1 ,··,M。

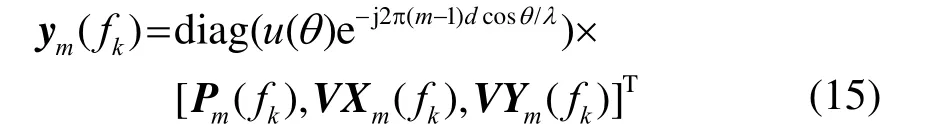
式中，Pm(fk)、VXm(fk)和VYm(fk)分别为pm(t)、vxm(t) 和vym(t)的傅里叶变换。

第n个子矢量阵的常规波束形成为

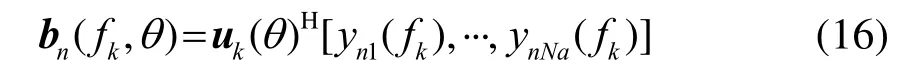
其中，yni(fk)表示第n个子阵中的第i个阵元信号经过相移后的值，n= 1 ,2,··,N，i= 1 ,2,··,Na。

N个子矢量阵常规波束输出向量为

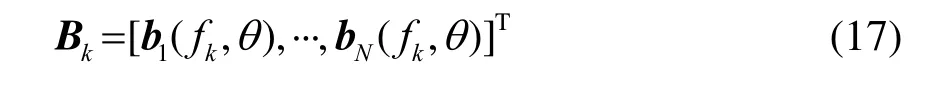
子矢量阵条件下的空间协方差矩阵为

其中Δf为处理的频带范围。

子阵域VSTMV波束形成的权向量为：

式中， 1N为N×1维单位向量。

子阵VSTMV频域输出为

由式(18)可以看出，通过子矢量阵VSTMV处理，空间协方差矩阵的维数由3M×3M维下降为N×N维，相对于VSTMV，大大降低了计算量，有利于工程上的实时实现。

4 仿真分析

仿真条件：二维矢量水听器个数为 16个，阵元间距为1.5 m，信号源为CW信号，中心频率为500Hz，加入高斯白噪声，分析带宽为 100~3000 Hz，采样率为16 kHz，将矢量阵分为4个子阵，每个子阵中有4个阵元，即子阵数N＝4，每个子阵中的阵元数Na＝4，所以每个子阵含有12路信号。

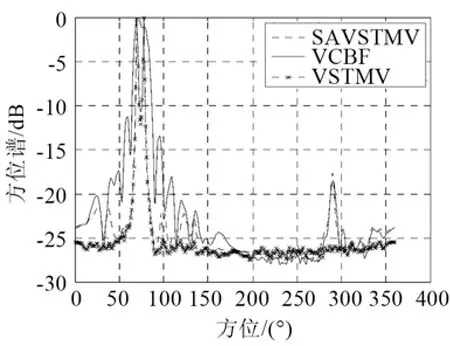
图2 SAVSTMV、VSTMV和VCBF波束输出(单目标, SNR: 10dB,方位 70°)Fig.2 Output patterns of SAVSTMV, VSTMV and VCBF(single target, SNR:10dB, azimuth: 70°)

图2为单目标仿真结果，其中SAVSTMV为子阵域VSTMV 的 波束形成算法，VCBF为矢量阵常规波束形成算法，VSTMV为阵元域矢量阵STMV波束形成算法。对比三种结果可以看出，SAVSTMV和VSTMV都比VCBF主瓣较窄，旁瓣也较低，提高了方位估计精度。SAVSTMV与VSTMV相比较，SAVSTMV的左右舷抑制比略低于 VSTMV，和VCBF的左右舷抑制比基本一样。

图3为双目标仿真结果，对比三种结果可以看出，对于两个方位较近的信号，VCBF算法不能够分辨出来，而SAVSTMV和VSTMV两种算法都能够分辨出来，但是SAVSTMV算法的左右舷抑制比低于 V STMV算法。

图3 SAVSTMV、VSTMV和VCBF波束输出(双目标, SNR: 10dB, 方位: [70, 78]°)Fig.3 Output patterns of SAVSTMV, VSTMV and VCBF (double target, SNR:10dB, azimuths: [70°,78°])

在实 际 试验和工作环境中，由于海流等其它因素可能会造成拖线阵的变形或者阵元损坏等情况，由此会影响波束形成的性能下降。通过对个别阵元信号置零来模拟阵元损坏情况，进行SAVSTMV和VSTMV的性能对比。将2号阵元、6号阵元信号置零，仿真结果如图4和图5所示。

图4和图5分别是单目标和双目标仿真结果。

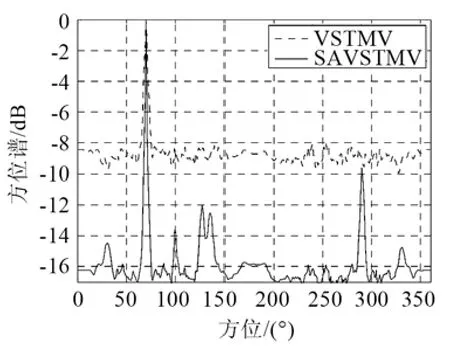
图4 稳健性比较(SNR: 10dB, 方位70°)Fig.4 Comparison of solidity robustness (single target, SNR: 10dB,azimuth: 70°)

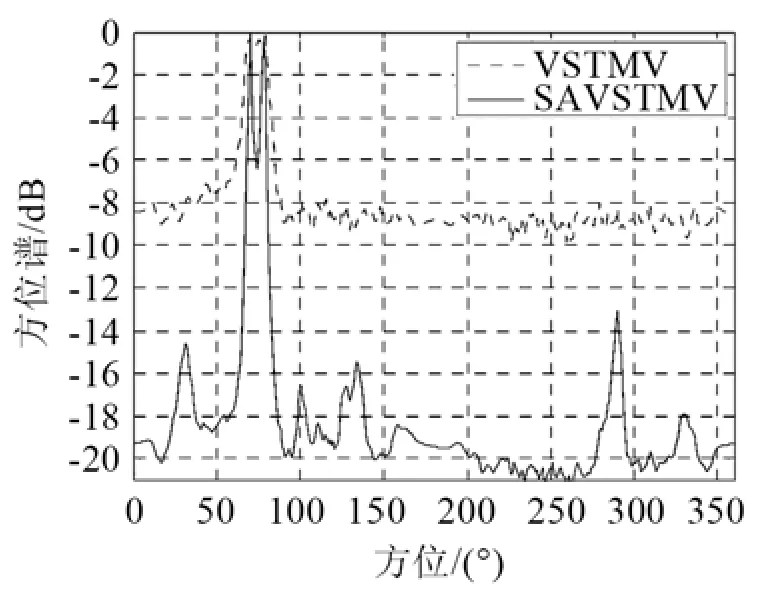
图5 稳健性比较(SNR: 10dB, 方位: [70, 78]°)Fig.5 Comparison of solidity robustness (double targets, SNR: 10dB,azimuths: [70°, 78°])

从图4和图5中可以看出，在矢量阵中阵元损坏的情况下，SAVSTMV算法要比VSTMV算法稳健性好，表现为主瓣窄，旁瓣级低，因此SAVSTMV比VSTMV具有较好的稳健性。

综上可以看出，SAVSTMV算法方位分辨率高，旁瓣级低，能够消除左右舷模糊现象，并且计算量低，稳健性好，有利于工程上的实时实现。

5 结 论

本文通过对矢量阵进行多子阵常规波束形成，然后再 进 行STMV自适应波束形成，从而降低了计算过程中数据协方差矩阵的计算量，并能有效提高算法稳健性。

仿真表明该算法能够分辨左右舷模糊现象，方位分辨力高，旁瓣级低，在部分阵元失效条件下仍具有较好性能，为工程上的应用具有一定的指导意义。

参考文献

[1] 周胜增, 杜选民. 快速收敛最小方差无畸变响应算法研究及应用[J]. 声学学报, 2009, 34(6): 515-520.ZHOU Shengzeng, DU Xuanmin. Research and application of fast-convergent minimum variance distortionless response algorithm [J]. Acta Acustica, 2009, 3 4(6): 515-520.

[2] 陈阳, 惠俊英. 声矢量阵导向最小方差波束形成算法研究[J]. 哈尔滨工程大学学报, 2008, 29(11): 1199-1204.CHEN Yang, HUI Junying. Acoustic vector-sensor array steered minimum variance beamforming[J]. Journal of Harbin Enginng University, 2008, 29(11): 1199-1204.

[3] 惠俊英, 惠娟. 矢量声信号处理基础[M].北京: 国防工业出版社,2009: 63-80.HUI Junying, HUI Juan. Elements of vector Acoustic singnal[M].Beijing: National Defense Industry Press, 2009: 63-80.

[4] 张揽月, 杨德森. 基于 MUSIC算法的矢量水听器阵源方位估计[J]. 哈尔滨工程大学学报, 2004, 25(1): 30-33.ZHANG Lanyue, YANG Desen. DOA estimstion based on MUSIC algorithm using an array of vector hydrophones[J]. Journal of Harbin Enginng University, 2004, 25(1): 30-33.