求任意阶递推关系通项的矩阵方法

赵晓苏，钱椿林

(苏州市职业大学 数理部，江苏 苏州 215104)

1 问题提出

在科学研究和生产实践中往往会遇到某些量之间存在着某种递推关系，其数学表达式为递推公式，例如

其中an-1，an，…，an+m-2，b0，b1，…bm-1(n=1，2，…；m=2，3，…)为常数.这是一种m阶常系数线性递推关系，具有形式简单、应用广泛等特点.文献[1]利用母函数和导数方法求二阶线性递推关系的通项，本文用矩阵方法将求二阶线性递推关系通项的问题推广到求任意阶递推关系通项的问题.具体方法是：首先将任意阶递推关系用矩阵表示，求其矩阵的特征值和特征向量，然后把矩阵对角化，最后利用矩阵乘法求得任意阶递推关系的通项[2-5].

2 问题解决

用矩阵方法求任意阶递推关系通项的具体步骤为：

第1步，将递推式(1)用矩阵表示为

则式(2)可记作

利用式(3)有

第2步，递推问题转化为求An.首先求出A的特征值与特征向量，然后将A对角化，最后求得An.

第3步，利用矩阵乘法，计算Un=AnU0.

第4步，取Un的第1行第1列的元素，得到un.

下面利用具体例子来说明用矩阵方法求任意阶递推关系通项的详细计算过程.

例1 裴波那契(Fibonacci)数列问题：如果1对兔子出生1个月后开始繁殖，每个月产生1对后代.现在有1对新生兔子，假定兔子只繁殖，没有死亡，那么问每月初会有多少兔子.

这对新生兔子出生时记为零月初，这时只有1对兔子，1个月后即1月初，还未开始繁殖，所以依然是1对.2月初，它们生了1对兔子，因此总共有2对兔子.3月初，它们又生了1对兔子，而在1月中生下的那对兔子还未繁殖，于是一共有3对兔子.如此继续下去，将每个月初兔子的数目排成一个数列，从0月初开始，一个月接着一个月排下去，即1，1，2，3，5，8，13，21，34，55，89，144，此数列称为裴波那契数列.

假定第n月初的兔子数为un，从裴波那契数列知

这是一个递推关系.显然初始值u0=1，u1=1.由此可递推出第n个月初兔子的数目，利用矩阵的特征值可以直接用一个显式来表达通项un.下面给出解题的具体步骤.

第1步，将式(4)用矩阵表示为

于是Un=AnU0.

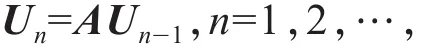
第2步，递推问题转化为求An.首先求出A的特征值与特征向量，即

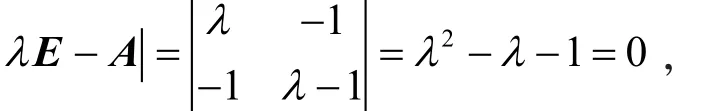
A的特征值为，相应的特征向量为.然后将A对角化，即

最后求An，有

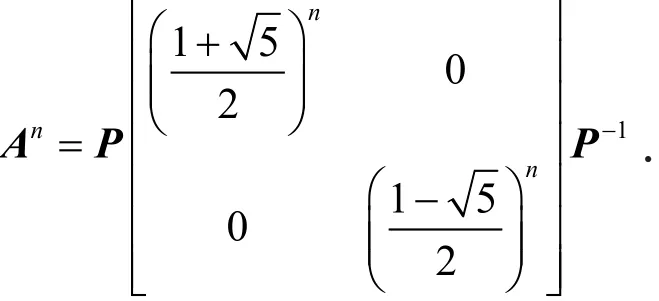
第3步，计算Un=AnU0.利用矩阵乘法，得

第4步，取Un的第1行第1列的元素，得到

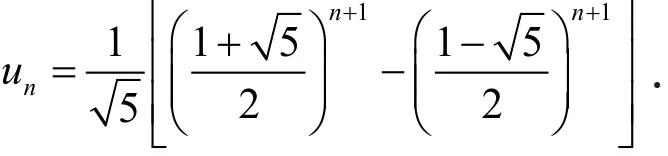
例2 设un+2=-6un-1+5un+2un+1(n≥1)，且满足u0=1，u1=2，u2=3，求通项un.

第1步，将递推关系un+2=-6un-1+5un+2un+1用矩阵表示为

令U且，则式(6)可记作Un=AUn-1，n=1，2，…，于是Un=AnU0.

第2步，递推问题转化为求An.首先求出A的特征值与特征向量，即

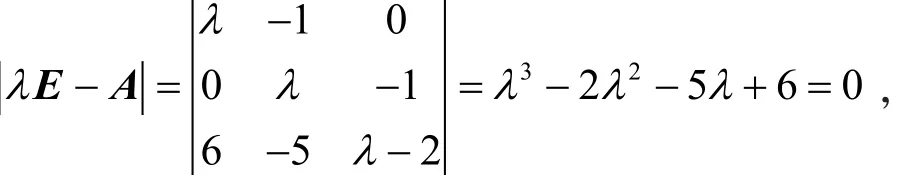
A的特征值为λ1=1，λ2=-2，λ3=3，相应的特征向量为，然后将A对角化，即

第3步，计算Un=AnU0.利用矩阵乘法，得

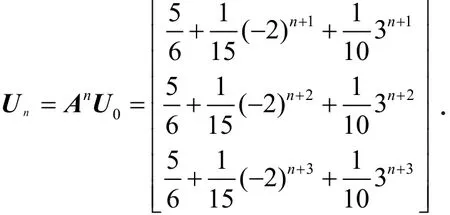
第4步，取Un的第1行第1列的元素，得到

[1]赵一鸣. 某类递推公式通项的一种解法[J]. 江苏广播电视大学学报，1995，13(1)：89-94.

[2]钱椿林. 线性代数[M]. 北京：高等教育出版社，2010.

[3]《现代应用数学手册》编委会. 现代应用分析卷[M].北京：清华大学出版社，1998.

[4]钱椿林. 高等数学[M]. 北京：电子工业出版社，2010.

[5]《数学手册》编写组. 数学手册[M]. 北京：高等教育出版社，1984：88-90.