基于数量折扣的改良品供应链协调策略

王 勇，孙海雷，陈晓旭

（1.重庆大学经济与工商管理学院，重庆 400030；2.重庆大学现代物流重庆市重点实验室，重庆 400030）

基于数量折扣的改良品供应链协调策略

王 勇1，2，孙海雷1，2，陈晓旭1，2

（1.重庆大学经济与工商管理学院，重庆 400030；2.重庆大学现代物流重庆市重点实验室，重庆 400030）

本文以改良品供应链为研究对象，采用数量折扣作为激励机制，研究了一个供应商和一个零售商构成的改良品二级供应链在批量对批量供应模式假设下的协调问题，以达到协调改良品供应链的目的。通过算例分析，发现基于数量折扣的改良品供应链协调策略有效地实现了改良品供应链的协调。最后对改良品供应链的改良率和市场需求率进行了敏感性分析，研究了它们对供应链的影响。

改良品；数量折扣；供应链协调

1 引言

最近几十年来，易变质品的研究受到了大量学者的高度关注。所谓的易变质品是指随着时间的推移而腐烂、损坏、挥发和过期而逐渐失去经济价值的商品，如牛奶、蔬菜、水果、肉食、鲜花、药品等。然而在市场中也存在随着时间的推移而质量得到改善或数量得到增加的商品，如养殖场或鱼塘中的生猪、鸡、鸭、鱼等。这类物品我们称之为改良品。

1997年，韩国人Hwang［1］首次研究了改良品库存问题，在改良率小于需求率和改良率大于需求率的情况下分别构造了EOQ模型和PSQ模型；此后，Hwang［2］在基于FIFO和LIFO两种策略下建立了PSQ模型和EPQ模型；后来，Hwang［3］又对改良品的仓库选址问题进行了研究；Moon等［4］在考虑通货膨胀与货币时间价值的情况下，结合改良和变质两种现象对库存的影响，建立了有限周期内需求时变的EOQ模型。Mondal［5］对物品同时发生改良和变质的库存问题进行了研究，假设物品改良率服从二个参数的威布尔分布，变质率恒定，需求率与价格相关，在饲养周期末，未售出的物品需做削价处理，建立了相应的改良品库存控制模型。Mondal［6］等考虑物品同时受改良和变质的影响，假设净改良率服从两个参数的威布尔分布，并随时间递减，建立了以重量为单位，价格影响需求率，瞬时补货且无短缺量拖后的改良品EOQ模型。Law等［7］从制造商和销售商的角度出发建立了一个整合的生产库存模型，该模型考虑了改良率和变质率的影响，同时也考虑了多次发货、部分延迟订货和时间折扣。Sana［8］研究了受企业积极性影响的时变需求，存储设施能力限制的关于变质品与改良品的多物品EOQ模型。而国内对改良品的研究比较少，陈晖等［9］以处于育肥期的生猪为研究对象，通过调查和实证模拟研究，找到其净改良规律以及市场需求特性，建立了生猪类改良品库存模型。

数量折扣合同由于其简单的可操作性而成为实践中最常用的供应链的协调与激励机制。Monahan［10］最早对供应链的数量折扣问题进行了研究，在基于批量对批量的假设下，在由单个卖方企业和买方企业构成的供应链中，提出了系统最优及卖方企业最优的数量折扣合同；Hau等［11］扩展了上述模型，通过增加数量折扣的限制条件，同时取消批量对批量的假设，因此使得模型的结论更具有一般意义。Weng［13］在价格影响最终需求的情况下，提出了面对同质零售商时，供应商的最优定价及数量折扣政策；Munson等［14］研究了包括供应商、制造商和零售商的三级供应链系统提出了三级供应链的数量折扣政策。需要指出的是上述研究均假设信息对称以及物品均未发生变质或者改良。Simone等［15］和孔洁宏等［16］都研究了完全信息时易腐品供应链的协调问题；曹宗宏等［17］研究了受库存水平影响需求的变质品的供应链，给出了可以协调供应链的数量折扣策略；而现在对改良品供应链的协调问题的研究则还没有出现。

在改良品供应链中存在这样的一类供应链：供应商与零售商之间的订货是采用批量对批量的模式，并且该类改良品在零售商的仓库中能够继续得到明显的改良，如孵化场向养殖场提供鸡苗、鸭苗、鹅苗时采用的就是批量对批量的模式，同时鸡苗、鸭苗、鹅苗在养殖场中将会得到持续的生长。本文就以该类改良品供应链作为研究对象，采用数量折扣作为激励机制，在批量对批量供应模式假设下，研究了改良品供应链协调策略问题，给出了最优订购策略。最后，通过算例分析，发现基于数量折扣的改良品供应链协调策略有效地实现了改良品供应链的协调，最后对改良品供应链的改良率和市场需求率进行了敏感性分析，研究了它们对供应链的影响。

2 模型

2.1 假设和参数说明

在由一个供应商和一个零售商的二级改良品供应链中，我们假设：供应商与零售商信息对称，供应商能够获得零售商的订货信息；供应商与零售商之间采用批量对批量的订货模式，供应商不考虑生产及原材料成本；市场需求率是常数；零售商的订货必须即时补充，不允许缺货；零售商在每个订货周期末的库存为零；商品在进入零售商的仓库后将得到改良，改良率恒定且大于0，经过改良之后的增加的商品将占有库存，同时不考虑商品的变质。

相关的参数说明如下。

D：商品的市场需求率；λ：改良品的改良率；Gr：零售商每次订货的固定成本；H：零售商的单位时间单位商品的库存成本；Ca：零售商的单位改良商品的改良成本；C：供应商给予零售商的单位商品批发价格（C＞Ca）；Q：零售商的订货批量；T：零售商的订货周期；Gs：供应商每次处理订单的固定成本；I（t）：t时刻零售商的库存水平；d（·）：供应商依据零售商的订货量给予的数量折扣；TC（·）：表示单位时间内的成本函数。

2.2 模型的建立

根据假设，参照易变质品在常变质率下的库存模型，在订货周期内t时刻的库存水平I（t）由于改良的作用而增加，同时由于需求的作用而减少。故满足微分方程：

解之得：

由式（3）可知当商品需求率D以及商品改良率λ固定时，订货批量Q与订货周期T存在一一对应关系。这种情况下，在分析供应链的协调问题时，以订货周期而非订货批量作为决策变量将会大幅度简化问题的分析，为此本文将以订货周期为决策变量。2.2.1 在分散决策下零售商与供应商的最优决策

在分散决策下，零售商的总成本由订货成本、采购成本、库存成本、改良成本四部分构成。其中：

（1）订货成本为：Gr

因此，每次的零售商的订货批量为：

（3）库存成本为：

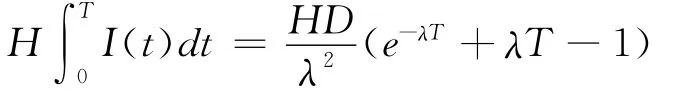
（4）改良成本为：

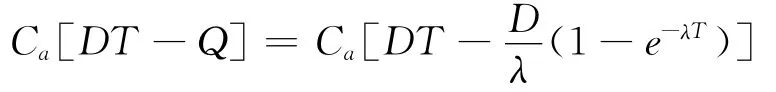
从而，零售商的单位时间的总成本为：

对上式直接求解最优解存在一定的难度，为此，将指数函数进行泰勒展开，并取其前三项［16，18］，即：

将式（5）代入式（4）可以化简为：

式（6）对T分别求一阶、二阶导数，有：

即为在分散决策下零售商的最优订货周期。

将式（7）分别代入式（3）与式（6），对应的在分散决策下最优订货批量及单位时间最低成本分别为：

对于供应商而言，由于采用批量对批量的供应模式，供应商将不会持有库存，故其购买成本为外生变量，可不予考虑。在分散决策下，供应商单位时间的成本函数为：

易知，为了使得供应商成本最小，T的取值应该尽可能地大。

本文中零售商处于主导地位，故当零售商按TD向供应商订货时，供应商的单位时间成本为：

此时，在分散决策下供应链的单位时间总成本为：

通过对式（7）、式（9）、式（11）、式（12）分别对λ求导，有：

由此可以得到以下定理：

定理1 在分散决策下，零售商的最优订货周期TD将随着改良率λ的增大而增大，零售商的单位时间最低总成本TCD1、供应商的单位时间成本TCD2、供应链的单位时间总成本TCD3将随着改良率λ的增大而减小。

2.2.2 集中决策下系统的最优决策

从集中决策的角度考虑，整个改良品供应链系统的单位时间总成本为：

式（13）分别对T求一阶、二阶导数，有：

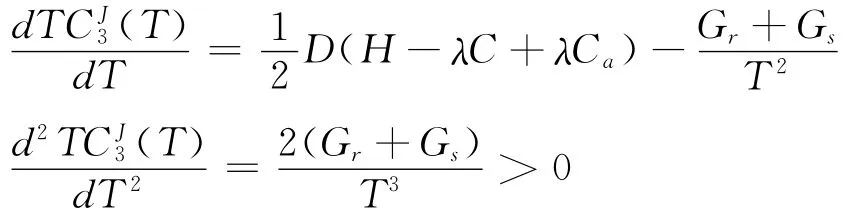
即为在集中决策下零售商的最优订货周期。

易知TJ＞TD，由此我们可以得到：在分散决策时，零售商虽然使得自己的成本最小化，但是由于未考虑其决策对供应商成本的影响，从而不能使得整个系统达到最优。

将式（14）代入式（3）和式（13）分别得到集中决策下系统的最优订货批量及单位时间的最低总成本分别为：

通过对式（14）和（16）分别对λ求导，有：

由此可以得到以下定理：

定理2 在集中决策下，供应链系统的最优订货周期TJ将随着改良率λ的增大而增大，系统的单位时间的最低总成本TC将随着改良率λ的增大而减小。

2.2.3 集中决策下的数量折扣模型

数量折扣合同由于其简单的可操作性而成为实践中最常用的供应链的协调与激励机制。为此，本文采用数量折扣合同来协调供应链。为了使得供应链协调，供应商将给予零售商合适的数量折扣，从而激励零售商将自有最优订货量提升至系统最优的订货量。当零售商改变订货策略后，其成本将会增加，遭受的损失应该得到供应商的补偿，补偿的金额必须大于等于零售商遭受的损失。供应商提供数量折扣后，零售商的成本至少要不高于分散决策下的最低成本。由此我们可以认为零售商可以接受的最高成本为TCD1。

供应商向零售商提供基于零售商采购数量的数量折扣合同d（Q），同时由于Q与T存在一一对应的关系，所以数量折扣合同又可转换成d（T）。所以对于供应商而言，最优数量折扣合同可通过求解如下规划问题获得：

根据式（17），在最优数量折扣合同中，对于给定的T，应满足：

也就是说供应商给予零售商的单位时间数量折扣总量要不小于零售商由于改变其订货批量而遭受的损失。然而，要使得供应商的单位时间成本最小，供应商给予零售商的单位时间数量折扣总量必须正好等于零售商的单位时间成本的增加，从而，式（18）的等号成立，将其代入式（17），规划问题转换为

将式（6）、式（9）和式（10）代入式（19），并求得其极值为

由式（20）可知，当零售商的订货周期与供应链系统最优的订货周期相同，并且将所有的协调收益分配给供应商时，此数量折扣合同为最优的合同，因此：

其中：

从而，在最优数量折扣合同下，零售商、供应商和供应链的单位时间总成本分别为：

式（22）和式（24）表明在零售商没有增加成本的前提下，最优数量折扣合同使得改良品供应链的总成本达到系统最低，从而实现了改良品供应链的协调。

通过对式（20）、式（22）、式（23）和式（24）分别对λ求导，有：

定理3 在最优数量折扣合同下，系统最优的订货周期TC随着改良率λ的增大而增大，零售商单位时间总成本TC、供应商单位时间总成本TC和供应链单位时间总成本TC随着改良率λ的增大而减小。

3 算例分析

假设在由一个供应商和一个零售商构成的二级改良品供应链中，相关参数如下：λ=0.05，D= 5000个/年；Gr=150元/次，Gs=200元/次，H= 6元/个，Ca=5元/个，C=10元/个。

3.1 最优数量折扣

将以上参数代入上述模型，分别计算出在分散决策、集中决策和基于数量折扣的集中决策下，零售商、供应商和供应链的各种类型成本及其变动情况，如表1所示。

表1 分散决策、集中决策和基于数量折扣的集中决策成本比较

从表1中我们可以看到在集中决策下，供应链的总成本比分散决策时有了显著的降低，这是由于零售商延长了订货周期，减少了订购次数，从而大幅度降低了供应商的单位时间处理订单成本。同时，由于零售商的单位时间库存成本和改良成本因其定货批量的增加而显著增大，在集中决策情况下，零售商成本不但没有降低，反而得到增加。因此，为实现供应链的协调，供应商需要通过给予零售商一定的补偿。通过供应商给予零售商合适的数量折扣，使得供应链系统实现了与集中决策下相同的最小总成本，同时零售商的成本也与分散式决策下相一致，而供应商的成本有了显著降低。从这个意义上讲，基于数量折扣的改良品供应链更加协调。

3.2 敏感性分析

3.2.1 改良率对供应链成本的影响

由于不同的改良品具有不同的改良率，我们给出了在不同改良率下，零售商、供应商和供应链的各种类型成本，如表2所示。

从表2可以看出，随着改良率的增加，零售商的改良成本上升，零售商的库存成本也上升较快，同时零售商的订货成本、采购成本下降，而零售商总成本下降。而对供应商而言，随着改良率的增加，其订货成本也呈下降趋势。供应商给予零售商的数量折扣也有所下降，从而供应商的总成本也逐步下降。基于数量折扣的集中式改良品供应链的总成本始终随着改良率的上升而下降。

3.2.2 市场需求率对供应链成本的影响

本文中我们假设产品的市场需求率是恒定不变的。但是在真实的社会生活中产品的价格、库存等因素均会影响到产品的市场需求，从而产品的市场需求率是不确定的。因此我们给出了在不同市场需求率下，零售商、供应商和供应链的各种类型成本，如表3所示。

表2 改良率对成本的敏感性分析

表3 市场需求率对成本的敏感性分析

从表3可以看出，随着商品的市场需求率的增加，零售商的订货成本、采购成本、库存成本、改良成本均得到了上升，其中零售商的采购成本上升幅度较大，而零售商总成本也呈现出上升的趋势。而对供应商而言，随着商品需求率的增加，其订货成本呈上升趋势，而供应商给予零售商的数量折扣也逐步上升，从而供应商的总成本也逐步上升。基于数量折扣的集中式改良品供应链的总成本始终随着市场需求率的增加而上升。

4 结语

本文在批量对批量的假设下，提出了基于数量折扣的改良品供应链的协调策略。从本文的分析可以得出，简单的集中决策并不能使得改良品供应链上所有的成员企业均受益。但是，通过以数量折扣作为激励机制，在零售商与供应商原有成本均没有增加的情况下，使得改良品供应链的总成本得到降低，从而实现了改良品供应链的协调。

在接下来的研究中，可以考虑取消批量对批量的假设、改良率及需求恒定的限制，将二级改良品供应链推广到三级改良品供应链等。

［1］Hwang H S.A study on inventory model for items with Weibull Ameliorating［J］.Computers and Industrial Engineering，1997，33（3）：701-704.

［2］Hwang H S.Inventory models for both deteriorating and ameliorating items［J］.Computers and Industrial Engineering，1999，37（1）：257-260.

［3］Hwang H S.A stochastic set-covering location and deteriorating items［J］.Computer and industrial Engineering，2004，46（2）：313-319.

［4］Moon I，Giri B C.Economic order quantity models for ameliorating/deteriorating items under inflation and time discounting［J］.European Journal of Operational Research，2005，162（3）：773-785.

［5］Mandal B，Bhunia A K，Maiti M.An inventory system ameliorating items for price dependent demand rate［J］. Computer and Industrial Engineering，2003，45（3）：443 -456.

［6］Mandal B，Bhunia A K，Maiti M.Inventory partial selling quantity model of ameliorating items with linear price dependent demand［J］.Advanced Modeling and Optimization，2005，7（1）：145-154.

［7］Law S T，Wee H M.An integrated productioninventory model for meliorating and deteriorating items taking account of time discounting［J］.Mathematical and Computer Modelling，2006，43：673-685.

［8］Sana S S.Demand influenced by enterprises′initiatives -A multi-item EOQ model of deteriorating and ameliorating items［J］.Mathematical and Computer Modelling，2010，52（1）：284-302.

［9］陈晖，罗兵，杨秀苔，等.生猪类改良物品库存管理理论及实证研究［J］.科技管理研究，2008，6：293-296.

［10］Monahan J P.A quantity discount pricing model to increase vendor profits［J］.Management Science，1984，30（6）：720-726.

［11］Hau L L，Rosenblatt M J.A genera lized quantity discount pricing model to increase supplier profits［J］. Management Science，1986，32（9）：1178-1185.

［12］Lal R，Staelin R.An approach for developing an optimal discount pricing policy［J］.Management Science，1984，30（12）：1524-1539.

［13］Weng Z K.Channel coordination and quantity discount［J］.Management Science，1995，41（9）：1509-1522.

［14］Munson C L，Rosenblatt M J.Coordinating a three-level supply chain with quantity discounts［J］.ⅡTransactions，2001，33：371-384.

［15］Simone Z，Lucio Z.Single-vendor single-buyer with integrated transport-inventory system：Models and heuristics in the case ofperishable goods［J］.Computers and Industrial Engineering，2007，52（1）：107-123.

［16］孔洁宏，骆建文.易变质品供应链的协调策略［J］.工业工程，2008，11（2）：96-101.

［17］曹宗宏，周永务.库存水平影响需求的变质性商品的供应链协调模型［J］.中国管理科学，2009，17（5）：61 -67.

［18］张钦红，赵泉午，熊中揩.不对称信息下的易逝品退货物流协调运作研究［J］.中国管理科学，2006，14（2）：107-111.

Supply Chain Coordination Strategy for Ameliorating Items Based on Quantity Discount

WANG Yong1，2，SUN Hai-lei1，2，CHEN Xiao-xu1，2
（1.School of Economics and Business Administration，Chongqing University，Chongqing 400030，China；2.Chongqing Key Laboratory of Logistics，Chngnqing University，Chngnqing 400030，China）

A two-echelon supply chain of ameliorating items consisting of a retailer and a supplier is presented in this paper to achieve the supply chain coordination.The coordination problem of the supply chain is studied by taking quantity discount as incentives under the assumption of the lot-for-lot policy.It can be found that the optimal strategy is achieved with quantity discount provided by the supplier.The numerical example is given to illustrate that the optimal strategy is very effective in improving the coordination of the supply chain.The sensitivity of the total cost of the supply chain with respect to amelioration rate and demand rate has also been presented at last.

ameliorating items；quantity discount；supply chain coordination

F274

：A

1003-207（2014）04-0051-07

2011-10-24；

2013-01-04

国家自然科学基金资助项目（71272085）；教育部人文社会科学研究规划基金资助项目（12YJA630135）

王勇（1957-），男（汉族），四川内江人，重庆大学经济与管理学院，教授，博士生导师，研究方向：物流与供应链管理.