基于灰色理论的自主式水下航行器舵机控制系统设计

吴正平 陈永亮 唐 念 俞 辉

（1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.三峡大学 理学院，湖北 宜昌 443002）

近年来，随着水下资源的开发以及军事上的需求，AUV的发展越来越受到关注.舵机作为AUV控制方向的执行机构，直接影响到AUV的总体控制性能.而电动舵机相对于气动、液动舵机控制简单、性能可靠，故在水下航行器中得到了广泛应用［1］.因舵机控制要求超调量很小（以一次性旋转到位为佳）、调节时间短，传统PID很难达到控制要求.文献［2］提出了分段式PID控制，即根据舵角偏差的大小选择不同的KP、KD系数，但是这种方法需要大量实验后的经验才能得到较好的分段系数，实现起来有一定的难度.文献［3］提出了改进的模糊PID控制算法，虽然可以改善模糊PID的控制性能，但是其隶属度函数的建立需要专家经验，较难根据实际环境得到合适的参数.文献［4］提出了一种基于DSP的模糊神经网络控制器，从仿真实验可以看出其控制效果较好，但是神经网络运算量大，计算复杂，并且稳定性还有待验证.文献［5］提出了一种灰色预测PID控制，其控制效果较好，易于实现，本文在其基础上加以改进，用于AUV舵机控制，仿真和实验均证明控制效果较好.

1 舵机控制系统总体方案

本课题设计的舵机控制器是用一个控制板来控制两路舵机：水平舵机和垂直舵机，其中水平舵机用来控制AUV的高度，垂直舵机用来控制AUV航行角度.舵机选用直流无刷电机，采用经典的三环控制［6］，即电流环、速度环和位置环，整体控制框图如图1所示.其中电流环作为内环，速度环作为中间环，位置环作为外环.STM32RCT6单片机自带18路12位AD采集通道和直接内存存取（DMA）模块，可用于快速AD采集和数字滤波；256KFlash存储器，可用来存储PID参数，1路CAN控制器，外接CAN接收器（MCP2551）即可实现CAN通信；2路12位DAC，可用于电机模拟量速度控制；多路I／O口，用于数字信号输入输出控制.

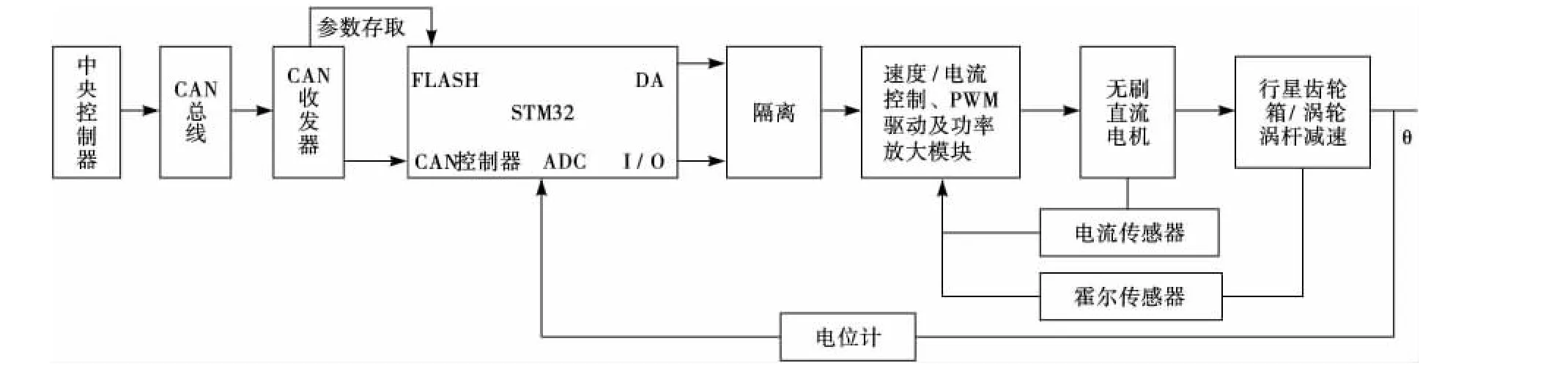
图1 直流电机三环控制框图

2 控制算法设计

2.1 PID算法

PID控制算法如下：

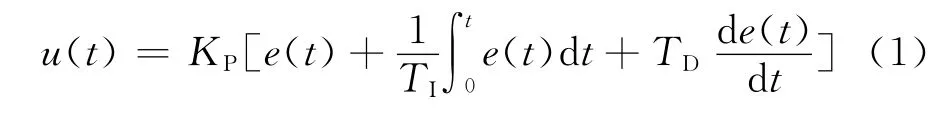
式中，u（t）为控制器输出，e（t）为控制器输入，KP为比例放大系数，TI为积分常数，TD为微分常数.

增量式数字控制器的输出只是控制量的增量ΔU，离散化后的PID算法如下：

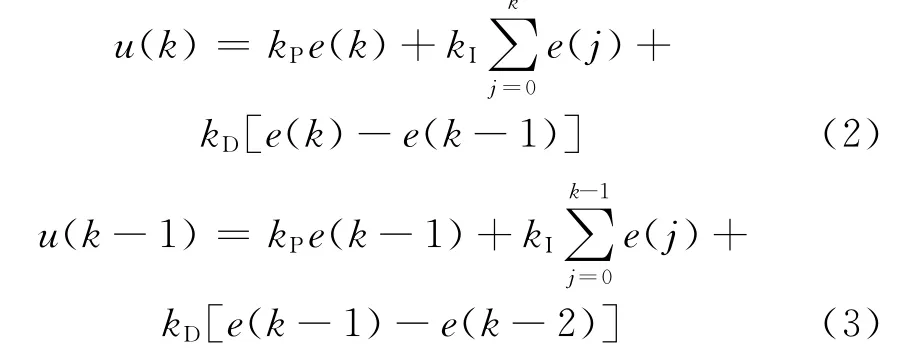
式（2）-式（3）可得

式（4）即为增量式PID的数学模型.增量式PID算法相对于位置式PID算法的优点是算式中不需要累加，控制增量u（k）的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果.

2.2 灰色模型

部分信息已知，部分信息未知的系统称为灰色系统［7］.灰色理论是对原始数据进行变换生成规则序列后再建模，从而预测事物未来的发展趋势.对于AUV舵机的控制，影响其控制性能的因素很多，而且干扰也随环境而变化，难以建立精确的控制模型.因此适合考虑以时间序列来构造灰色预测模型，根据系统未来的行为趋势进行相应的控制决策和预测控制.在灰色系统理论中，灰色模型是由一组灰色微分方程组成的动态模型，记为GM（n，h）.其中：n为微分方程的阶数，h为变量个数.灰色模型中应用较为广泛是的GM（1，1）模型，该模型由一个单变量一阶微分方程构成.下面用GM（1，1）来描述灰色系统建模过程.假设原 始 数 据 为 X（0）＝ （X（0）（1），X（0）（2），…，X（0）（n）），一阶累加后生成新的序列X（1）＝（X（1）（1），X（1）（2），…，X（1）（n）），其中：X（1）（i）＝2，…，n，则X（1）序列具有指数增长的规律，即满足一阶线性微分方程

Z（1）（k）为 X（1）的紧邻生成序列，Z（1）（k）＝0.5 X（1）（k）＋0.5 X（1）（k＋1），k＝1，2，3，…n.

得累加生成序列的灰色方程：

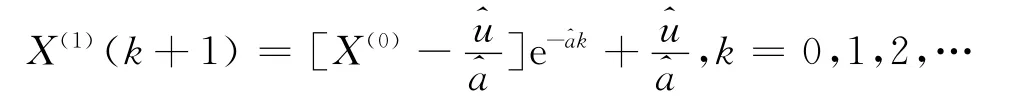
再对此式做累减还原，可得X（0）的灰色方程：

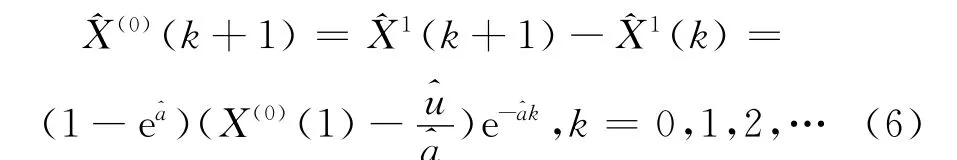
当k＝n-1时，式（6）为灰色滤波方程，当k＞n-1时，式（6）为灰色预测方程.

2.3 灰色PID

文献［5］提出使用灰色预测对PID反馈量进行处理，用预测采样值代替真实采样值，控制框图如图2所示.

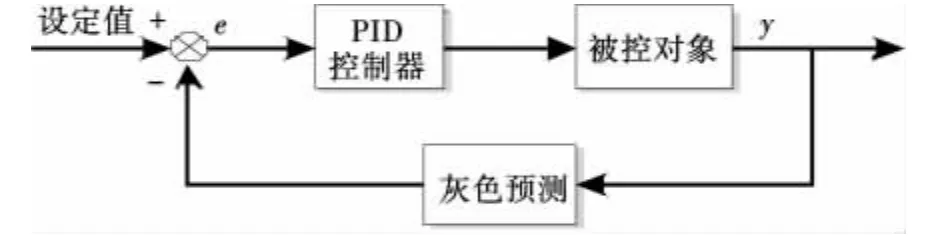
图2 灰色预测控制框图

舵机控制系统的广义动态特性的数学模型可以通过实验的方法得到，即用舵机转速阶跃扰动实验，获取电机转速变化曲线，然后用工程法拟合舵机广义数学模型.通过实验，使用舵机二阶简化模型：G（s）＝进行仿真，经过测试，选择灰色预测建模维数m＝4，使用上述控制方式进行Matlab仿真，用s函数编写灰色预测环节用于Simulink中，系统阶跃响应曲线和误差曲线如图3和图4所示.

图3 灰色预测控制系统阶跃响应曲线

图4 灰色预测控制系统 误差曲线

从曲线可以看出，灰色预测PID相比于常规PID超调量稍有减小，系统调节时间与常规PID相近，上升时间增加，控制效果基本没有得到改善.考虑到其误差曲线在拐弯处存在滞后性，在误差变化趋势发生改变时，其预测值与实际值偏差较大，曲线不平滑，选择在灰色预测之后加入灰色滤波器，控制框图如图5所示.

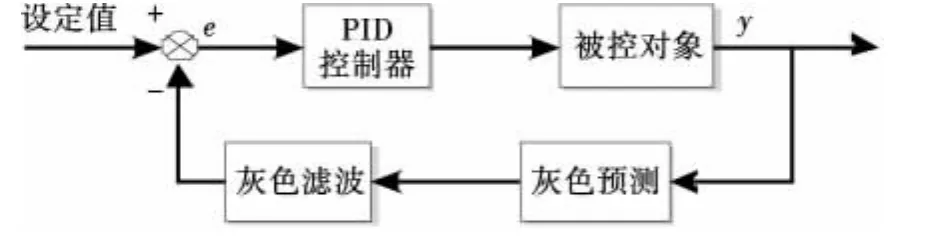
图5 改进灰色预测控制框图

灰色预测和灰色滤波均选用4阶模型，系统阶跃响应曲线和误差曲线如图6和图7所示.

图6 改进灰色预测控制阶跃响应曲线

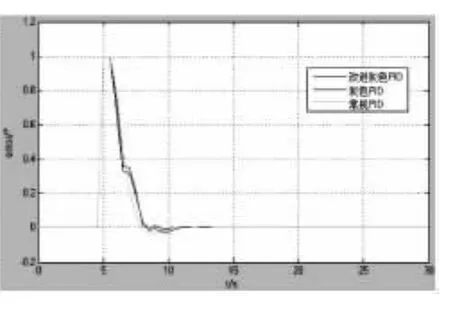
图7 改进灰色预测控制 系统误差曲线

由仿真曲线可以看出，加了灰色滤波器之后，误差跟踪性能得到提升，PID调节性能也随之改善.

3 实验及结论

将上述控制方法用于自主研发AUV的舵机控制系统中，用STM32单片机编程实现，实际控制效果如图8中“性能分析”部分所示.

图8 测试主控界面

图8为系统调试上位机界面.右边“性能分析”部分为使舵机输出角度为1°时舵机实时采样位置曲线，其中横坐标为时间，纵坐标为实际角度.实际要求舵机控制精度为±0.2°，从图中曲线可以看出，采用灰色预测与灰色滤波控制方式控制的超调量小，可将舵机位置精度控制在0.1°，响应速度较快，曲线较为平稳，能够满足实际控制要求.

［1］徐德民.鱼雷自动控制系统［M］.2版.西安：西北工业大学出版社，2001.

［2］李 霞，苏渊博.基于AVR单片机的电动舵机控制器设计［J］.单片机与嵌入式系统应用，2013，13（5）：67-69.

［3］王 迪，严卫生，付江峰.模糊控制在AUV舵机控制系统中的应用［J］.2009，34（12）：163-165.

［4］刘海涛，许 晖，流诗林.基于DSP的无刷舵用电机智能控制系统设计［J］.国外电子测量技术，2011，30（2）：67-69.

［5］黄春岑，与向军，吕震中.基于灰色预测PID球磨机负荷控制［J］.自动化仪表，2007（3）：62-64.

［6］张爱军.基于DSP＋CPLD的无刷直流电机三环控制设计［J］.电力电子技术，2012，46（11）：106-108.

［7］邓聚龙.灰色预测与决策［M］.武汉：华中工学院出版社，1986.