初始孔隙比对饱和砂土动力特性影响研究
曹久亭 孙阳光 黄思杰 刘夫江 刘 辰 刘春伟
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,南京 210098;2.河海大学 安全与防灾工程研究所,南京 210098;3.河海大学 岩土工程科学研究所,南京 210098;4.山东临沂水利工程总公司,山东 临沂 276006;5.临沂南水北调办公室,山东 临沂 276000)
砂土的物理状态和初始结构性控制着其强度和变形特性,国内外学者通过实验研究对土体的动力特性开展了大量研究工作,反映土体的物理参数主要有有效上覆压力、应力历史、密度、含水量、颗粒级配以及孔隙比或相对密实度等[1-3],土体的强度和变形特性起主要影响,其中孔隙比是一个相对重要的指标,尤其对于砂土来说,孔隙比或者相对密度可能是影响其强度的最重要因素.目前,大多数研究是基于砂土的物理状态变量[4-7]来研究砂土抗液化特性,因此关于物理状态变量对砂土抗液化能力有了很好的认识.
此外,仅有一些研究是关于初始结构性对砂土的抗液化能力的影响.郭莹[8]进行了相对密实度分别为70%、28%的密砂和松砂液化强度实验.曾长女等[9]探讨了黏粒含量和粉粒含量对重塑粉土动孔压发展的影响,结果表明,细粒含量对粉土动孔压发展影响较大.Yilmaz等[10]从极限孔隙比和孔隙比范围(emaxemin)研究砂土液化特性,结果表明平均粒径越小,砂土越容易液化;平均粒径相同或相近时,孔隙比范围越小,砂土越容易液化.
本文以四川汶川细砂为研究对象,在等压固结下对饱和砂土进行了不同围压和循环应力比下的不排水动三轴试验,研究了考虑不同初始孔隙比对饱和砂土的强度和孔压特性的影响,建立了动抗剪强度与有效围压之间的关系,并比较初始孔隙比和循环应力比对孔压特性的影响,为该地区在实际工程中的应用和计算提供借鉴和参考.
1 试验设备与试样
动三轴试验仪器为天水红山试验机有限公司研制生产的TAJ-20动三轴仪器,该仪器为电液伺服闭环控制系统,其幅频特性好,频率响应快,由主机、液压源、电控系统、计算机4大部分组成.
土样取自四川汶川某一边坡坡脚,在汶川地区极具代表性,所有试样为重塑试样,其颗粒筛分试验结果如图1所示.其不均匀系数Cu=3.25,曲率系数Cc=0.69,特征粒径d50=0.26mm,比重Gs=2.66,最大孔隙比emax=1.15,最小孔隙比emin=0.62,由颗粒筛分试验结果可知,该土定名为细砂.采用3种不同干密度试样ρd分别为1.4g/cm3、1.5g/cm3、1.6g/cm3,初始孔隙比e分别为0.90、0.77和0.66.

图1 汶川砂土颗粒筛分试验曲线
2 试验过程与方法
试验采用直径39.1mm,高度为80mm的重塑土样.重塑试样的制备为多层湿捣法,分5层击实,根据土样的干密度和预先设计的含水量确定每层土样的重量,击实到相应高度,各层接触面刮毛以保证上下接触良好,制备完成后安装到循环三轴仪的压力室内.在三轴压力室内联合抽真空、通无气水和加反压两种方法饱和,这样避免了试样在放入真空饱和缸时对试样的扰动,当孔隙水压力系数B值≥0.95时,认为试样满足饱和度要求.然后进入固结阶段,所有试样均为等压固结.固结完成后,进入振动阶段.试验计算机中适时监视试验过程,并记录试验过程中的轴向力、应力和孔隙压力.破坏标准取孔压等于围压,对于密实砂不能液化时,取双幅应变达到5%作为补充.
3 试验结果与分析
3.1 动强度特性
根据破坏标准,找出试样破坏时对应的循环次数,如图2所示为动应力σd随破坏振次Nf的变化关系,可以看出,饱和砂土的动强度随围压增大而增加,在同一围压下随着应力的降低,破坏振次逐渐增大,曲线降低速率由快变慢,最后σd-Nf曲线趋于稳定;在相同的破坏振次下饱和砂土的动强度随围压增大而增加.细砂的σd-Nf关系可用式σd=a+blnNf表示,式中:a、b为拟合参数,对本试验的不同围压和不同初始孔隙比细砂试样a和b见表1.

图2 动应力σd与破坏振次Nf的关系
循环应力比(CSR)定义为CSR=σd/2σ3,式中:σd为轴向动应力,σ3为围压.图3(a)为孔隙比e为0.77时不同围压下CSR-Nf关系曲线,由图可知,不同围压下砂土的试验数据点皆分布在较窄的范围内,围压对循环应力比的影响很小,可以近似地归一,随着破坏振次的增大,循环应力比线性减小.图3(b)为当围压为200kPa时不同初始孔隙比的CSR-Nf关系图,由图可知,循环应力比一定时,初始孔隙比越小,破坏振次越高.破坏振次一定时,初始孔隙比越大,液化所需的循环应力比越小.

表1 拟合参数a和参数b值

图3 细砂的CSR-Nf曲线图
3.2 动强度总应力参数
一定振次下动剪应力τd与围压σ3的关系可以表示为

式中,cd为动粘聚力,φd为动内摩擦角.一般来说,对于饱和砂土cd=0.
根据不同围压下细砂的σd-Nf关系拟合曲线表达式计算出固定破坏振次分别为10、20、30次时相应的动应力σd,根据动剪应力τd=σd/2,其中τd为试验动加载过程中试样45°面上的动剪应力幅,固定破坏振次分别为10、20和30次时动剪应力随围压变化关系,如图4所示.

图4 不同振次下动剪应力随有效围压的变化
图5给出了破坏振次Nf分别为10、20、30时饱和砂土的内摩擦角φd的数值,结果表明:孔隙比一定时随着破坏振次的增大,动内摩擦角降低,抗液化能力越弱;在相同破坏振次下,孔隙比越小,动内摩擦角越大,砂土的抗液化能力越强;在相同振次下,孔隙比为0.66的动内摩擦角比孔隙比为0.90的动内摩擦角提高了20%左右.
3.3 动孔压特性

图5 动内摩擦角φd与孔隙比e关系图
从孔压随循环次数的变化和一定循环次数液化(Δu=σ3)所需的循环应力比(CSR)两种角度来研究抗液化能力.图6给出了当σ3为200kPa,CSR为0.25时3种不同初始孔隙比孔压比(Δu/σ3)随循环次数(N)的变化情况,可以看出:对于孔隙比为0.66密实砂,孔压发展很慢,而孔隙比为0.90中密砂很容易液化;而孔隙比为0.90中密砂在循环20次时发生液化,而孔隙比为0.77的密实砂在循环40次时发生液化;还可看出即使孔隙比为0.77和为0.66均为密砂,抗液化能力却表现不同.

图6 初始孔隙比对饱和砂土孔压的影响
图7给出了围压为200kPa时循环次数分别为为10、20和30时孔压比与循环应力比关系图.由图7可知,随着试样变疏松,即随着初始空隙比的增大,曲线坡度逐渐增大,不同孔隙比的曲线坡度最大降低值高达50%;当循环10次时,循环应力比为0.27能引起孔隙比为0.90砂土液化,循环应力比为0.3能引起孔隙比为0.77砂土液化;当循环20次时,孔隙比为0.90和0.77的砂在循环应力比为0.24和0.27时接近液化,当循环30次时,孔隙比为0.90和0.77的砂在循环应力比为0.20和0.25时接近液化.可以看出,相对密实度对砂土液化抗力有着显著影响,孔压的发展取决于初始孔隙比,循环应力比越高时,表现得越明显,并且越容易发生液化破坏.
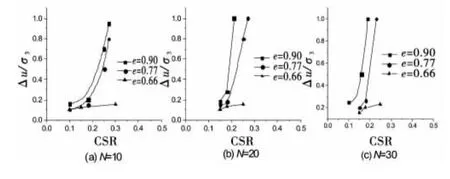
图7 一定循环次数时初始孔隙比和循环应力比对孔压的影响
4 结 论
本文在等压固结下,对汶川细砂进行了不同围压和循环应力比下的不排水动三轴试验,研究了考虑不同初始孔隙比对饱和砂土的强度和孔压特性的影响,研究表明:
1)饱和砂土的液化强度随围压增大而增加,在同一围压下随着动荷载的降低,破坏振次逐渐增大,曲线降低速率由快变慢,最后曲线趋于稳定;在相同的破坏振次下饱和砂土的液化强度随围压增大而增加.在一定循环应力比范围内,围压对砂土的循环应力比与破坏振次关系曲线影响不明显.
2)通过一系列试验,分析了不同初始孔隙比对饱和砂土动力特性的影响,建立了动抗剪强度与有效围压之间的关系;动内摩擦角与初始孔隙比之间的关系,孔隙比一定时随着破坏振次的增大,动内摩擦角降低,抗液化能力越弱;在相同破坏振次下,孔隙比越小,动内摩擦角越大,砂土的抗液化能力越强.
3)从孔压随振动次数变化和一定循环次数下液化所需的循环应力比两种角度来研究孔压特性,可以看出,初始孔隙比对砂土液化抗力有着显著影响,孔压的发展取决于初始孔隙比,循环应力比越高时,表现得越明显,并且越容易发生液化破坏.
[1]Cho G C,Dodds J,Santamarina J C.Particle Shape Effects on Packing Density,Stiffness,and Strength:Natural and Crushed Sands[J].J.Geotech.Geoenviron.Eng.,2006,132(5):591-602.
[2]Wichtmann T,Triantafyllidis T.Influence of the Grain-Size Distribution Curve of Quartz Sand on the Small Strain Shear Modulus Gmax[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(10):1404-1418.
[3]王星华,周海林.砂土液化动稳态强度分析[J].岩石力学与工程学报,2003,22(1):96-102.
[4]Ishibashi I,Kawamura M,Bhatia S K.Effect of Initial Shear on Cyclic Behavior of Sand[J].J.Geotech.Engrg.,1985,111(12):1395-1410.
[5]Bouferra R,Benseddiq N,Shahrour I.Saturation and Preloading Effects on the Cyclic Behavior of Sand[J].Int.J.Geomech.,2007,7(5):396-401.
[6]Ghionna V N,Porcino D.Liquefaction Resistance of Undisturbed and Reconstituted Samples of a Natural Coarse Sand from Undrained Cyclic Triaxial Tests[J].J.Geotech.Geoenviron.Eng.,2006,132(2):194-202.
[7]De Gennaro V,Canou J,Dupla J C,et al.Influence of Loading Path on the Undrained Behaviour of a Medium Loose Sand[J].Can.Geotech.J.,2004,41(1):166-180.
[8]郭 莹,贺 林.振动频率对饱和砂土液化强度的影响[J].防灾减灾工程学报,2009,29(6):618-623.
[9]曾长女,刘汉龙,陈育民.细粒含量对粉土动孔压发展模式影响的试验研究[J].岩土力学,2008,29(8):2193-2198.
[10]Yilmaz Y,Mollamahmutoglu M.Characterization of Liquefaction Susceptibility of Sands by Means of Extreme Void Ratios and/or Void Ratio Rang[J].Journal of Geotechnical and Geoenvironmental Engineering,2009,135(12):1986-1990.

