泡点压力处地层原油黏度预测
张 可,李 实,马德胜,陈兴隆
(提高石油采收率国家重点实验室 中油勘探开发研究院,北京 100083)
引 言
黏度参数是表征流体相态特征和流动特征的一个重要参数,同时也是油藏开发方案设计的关键工程参数之一。由于现场取样条件、经济成本等因素的制约,实验室有时无法直接获得具有代表性的地层流体样品,无法直接测得地层条件下的原油黏度值,给油藏数值模拟和开发方案的调整带来了较大的影响。目前,间接获得地层原油黏度的计算方法主要有经验关系式和状态方程法。状态方程法主要通过计算机进行反复迭代运算预测含气原油黏度,而对于地面脱气原油则无法预测,且该方法要求参数较多、耗时长、对计算机配制要求较高。预测地面脱气原油的关系式主要有:Beal[1]、Beggs-Robinson[2]、Glaso[3]、Labedi[4]、Kartoatmodjo-Schmidt[5];预测地层泡点压力点处原油的关系式主要有:Chew-Connally、Beggs-Robinson、Kartoatmodjo-Schmidt、Labedi[6]。根据参数选择特点一般可将经验关系式分为2类,一类是根据国内特定油田或区块进行回归的,针对性强、应用范围有限[7-11];另一类是根据国外特定油田或区块数据回归的,对国外数据吻合较好,对中国油田数据偏差较大[12-14]。因此,本文在总结前人研究成果的基础上,利用多元回归法,发展了预测地层原油黏度的经验关系式,解决了国外公式对中国原油黏度预测精度低的难题。
1 实验装置
PVT装置为法国ST公司生产的超高压可视相态装置,型号为PVT-240/1500FV,最高测试压力为150 MPa,最高测试温度为200 ℃,最大容积为240 mL。黏度测量装置为西安石天公司生产的落球式黏度计,最高测试压力为70 MPa,最高测试温度为100 ℃,最大容积为20 mL。密度计为安东帕公司生产,型号为DMA4500。
2 黏度模型建立
模型采用实验室10余年积累的完整PVT测试报告数据,该数据包括:泡点压力、地层温度、地面脱气油密度、不同压力条件下地层油黏度、气油比等,并涵盖国内样品(大庆、吉林、辽河、新疆、渤海、青海、华北、长庆)58个、国外样品(康菲、科麦琪、尼日尔、乍得、苏丹)共210个。此外,引用文献数据55个。
通过对数据分析,泡点压力处黏度与对应温度下地面脱气油黏度在对数坐标下存在一定的线性关系(图1)。
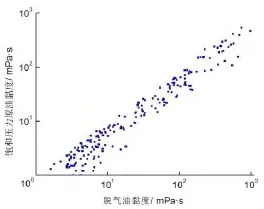
图1 泡点压力处黏度与脱气油黏度关系
2.1 国内外通用公式
选取国内外黏度数据,利用多元非线性回归法(麦夸特法和通用全局优化法)得出式(1)。公式样本范围:地面油黏度为1.6~980.0 mPa·s,气油比为0.3~255.8 m3/m3。

式中:μob为泡点压力处地层油黏度,mPa·s;GOR为气油比,m3/m3;μod为油藏温度下地面脱气油黏度,mPa·s;a=0.887 60,b=-0.159 47,c=0.967 18。
式(1)与4种预测方程(Chew-Connally、Beggs-Robinson、Kartoatmodjo-Schmidt、Labedi)进行误差对比(表1)。由表1可知,根据特定油田或区块样品得出的方程最大平均相对误差为 757%,最大绝对误差为 326%,最大均方根为 644.47%,最大标准差为85.25%。
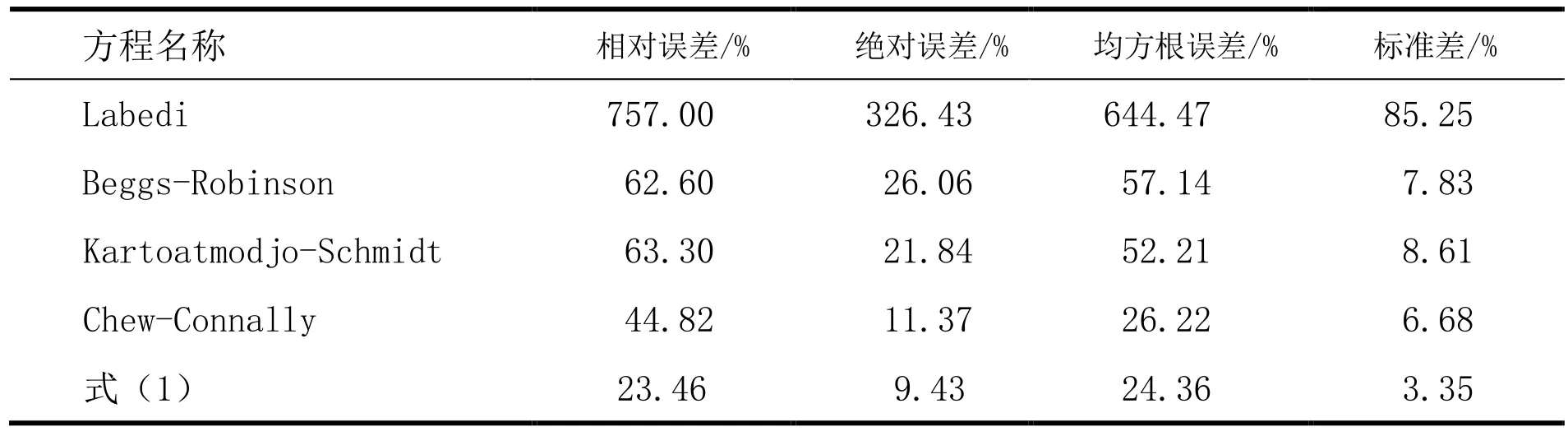
表1 泡点压力点原油粘度预测方程误差
2.2 国内样本公式
选取国内黏度数据,利用多元非线性回归法(麦夸特法和通用全局优化法)得出式(2)。公式样本范围:地面油黏度为1.56~659.00 mPa·s,气油比为7.7~255.8 m3/m3。

式中:d=4.656 70,e=-0.484 12,f=0.775 99。
式(2)与4种预测方程(Chew-Connally、Beggs-Robinson、Kartoatmodjo-Schmidt、Labedi)进行误差对比(表2)。由表2可知,式(2)预测关系式的相对误差、绝对误差、均方根误差、标准差值都远远小于现有预测公式,说明该公式预测精度较高、系统偏差较小。
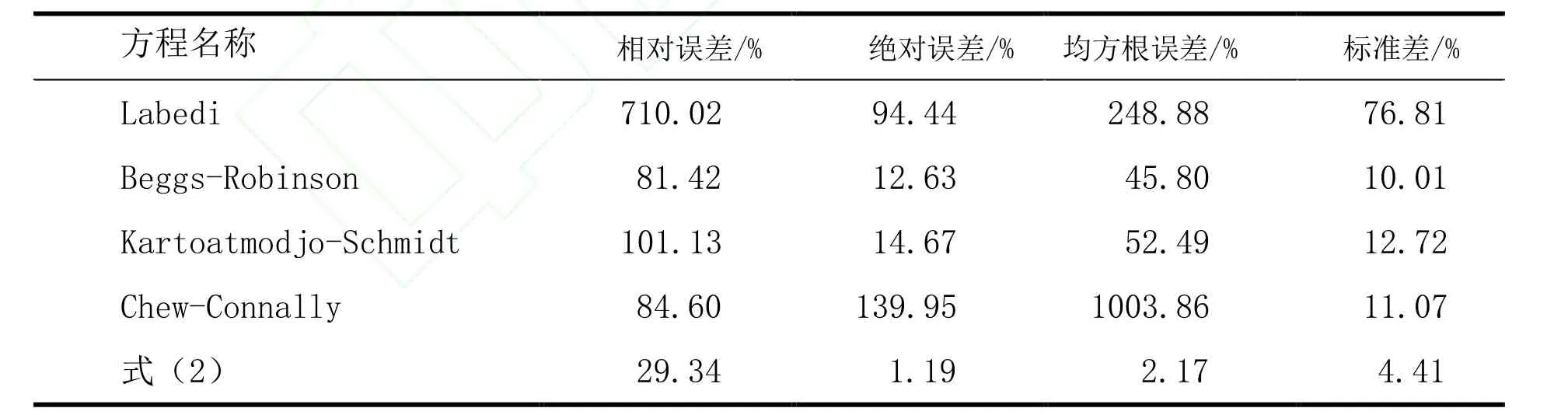
表2 泡点压力点原油黏度预测方程误差
3 模型准确性分析
3.1 通用公式准确性
由图 2可知,与同类预测关系式相比,式(1)具有最小误差分布和分散度,误差满足工程要求。五个预测关系式平均相对误差的由大到小关系为:Labedi>Kartoatmodjo-Schmidt> Beggs-Robinson > Chew-Connally>式(1)。其中,Chew-Connally的平均相对误差与式(1)较为接近。但其相对误差、绝对误差、均方根误差均高于式(1)。式(1)在的平均相对误差分布较为均匀,处于-50--+50之间,说明预测偏差分布合理。
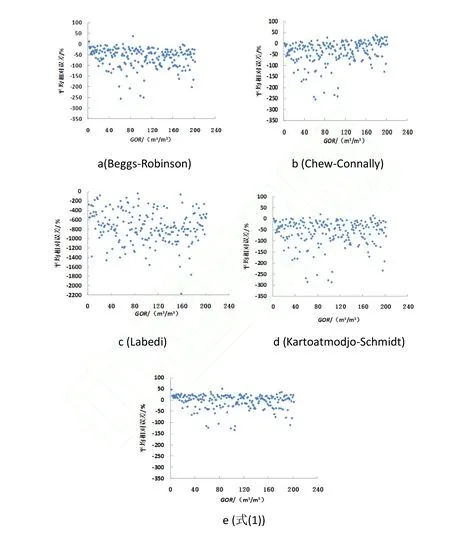
图2 泡点压力点黏度模型误差分布
3.2 国内样本公式准确性
由图3和表2可知,与同类预测关系式相比,式(2)具有最小的相对误差分布和分散度,误差满足工程要求。五个预测关系式平均相对误差的由大到小关系为:Labedi>Beggs-Robinson > Kartoatmodjo-Schmidt> Chew-Connally>式(2)。其中,Chew-Connally的平均相对误差与式(1)较为接近。但其相对误差、绝对误差、均方根误差均高于式(1)。Labedi始终处于负平均相对误差,其具有最大的平均相对误差。式(1)在的平均相对误差分布较为均匀,处于-50--+50之间,说明预测偏差分布合理。
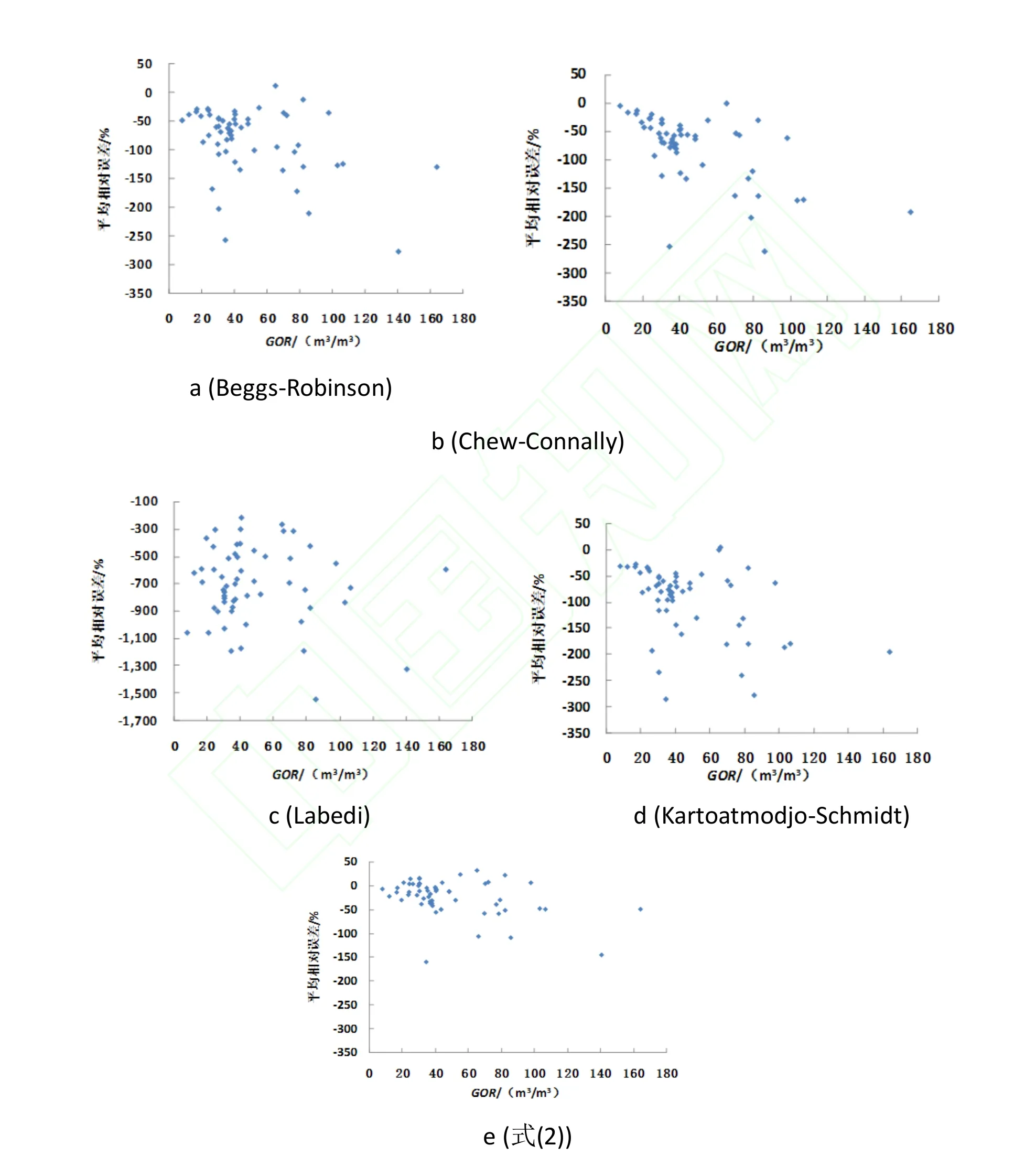
图3 泡点压力处黏度模型误差分布(国内通用公式)
4 结 论
(1)归纳总结了目前主要预测泡点压力处原油黏度的公式,并分析了已有公式提出的背景及适用条件。
(2)在测试 300余个地层油样品的高压物性及黏度的基础上,提出预测油藏条件下泡点压力点处地层油黏度关系式(国内外通用关系式和国内原油通用关系式),一定程度上填补了适应我国原油性质的通用关系式的空白。
(3)通过与现有的黏度关系对比,提出的黏度预测关系式形式简单,便于快速计算,预测精度满足工程要求,同时为油藏工程方案设计及数值模拟器的修改完善提供了可靠的黏度关系式。
[1]Beal C. Viscosity of air, water, natural gases, crude oil and its associated gases at oil field temperature and pressures[J].Trans AⅠME (Am Ⅰnst Min Metall),1946,165(3):114-127.
[2]Beggs H D, Robinson J R. Estimating the viscosity of crude oil systems[J].J Pet Technol,1975,27:1140-1141.
[3]Glaso O. Generalized pressure–volume–temperature correlation for crude oil system[J]. J Pet Technol,1980,2:785-795.
[4]Labedi R. Ⅰmproved correlations for predicting the viscosity of light crudes[J]. J Pet Sci Engng,1992,8(7):221-234.
[5]Kartoatmodjo F,Schmidt Z. Large data bank improves crude physical property correlation[J].Oil and Gas J,1994,4(1):51-55.
[6]Egbogah E O, Ng J T. An improved temperature viscosity correlation for crude oil systems [J]. J Pet Sci Engng,1990,5(11):197-200.
[7]Al-Maamari Rashid S,Houache O,Abdul-Wahab S A. New correlating parameter for the viscosity of heavy crude oils[J]. Energy and fuels,2006,20(9):2586-2592.
[8]Bergman,D.F.,Sutton,R.P.An update to viscosity correlations for gas-saturated crude oil [C],SPE Annual Technical Conference and Exhibition.Society of PetroleumEngineers, Anaheim, California, U.S.A.2007:187-190.
[9]康志勇,张勇. 辽河油区计算稠油黏度通用方程[J]. 特种油气藏,2005,12(6):101-102.
[10]王继强,樊灵,韩岐清,等. 大港油田高凝高粘度原油特性[J]. 油气地质与采收率,2007,14(6):94-96.
[11]唐晓旭,王闯,卢祥国,等. CO2混相驱注入能力预测理论研究及实例分析[J].大庆石油地质与开发,2011,30(3):150-153.
[12]王慧芳,何燕玲,郭新华. 含 CO2原油体系粘度测定与预测[J]. 油气地质与采收率,2009,16(3):82-84.
[13]王继强,樊灵,韩岐清,等. 大港油田高凝高粘度原油特性[J]. 油气地质与采收率,2007,14(6):94-96.
[14]吴永彬,赵欣,韩静,等. 委内瑞拉超重泡沫油泡沫强度实验研究[J]. 特种油气藏,2012,19(3):93-96.

