一个非齐次核的半离散型Hilbert型不等式的改进

贺乐平,刘 妥



一个非齐次核的半离散型Hilbert型不等式的改进

贺乐平*,刘 妥

(吉首大学 数学与统计学院, 湖南 吉首, 416000)

式(1)称为Hardy-Hilbert积分不等式, 它在分析学中有重要的应用.

文献[1]给出了如下一个新的较精确的半离散Hilbert不等式:

1 引理及证明

为了方便起见, 先介绍一些符号:

证明见文献[2].

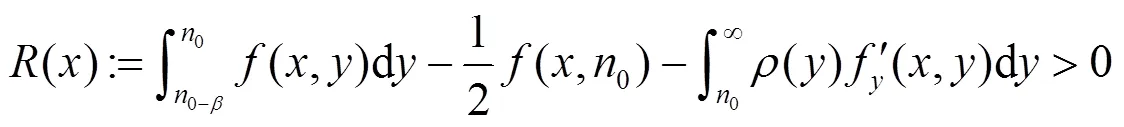
证明过程见文献[2].

2 主要结果

为方便起见, 再引入一些符号:

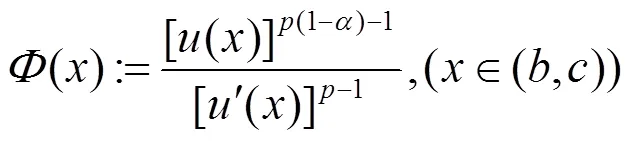
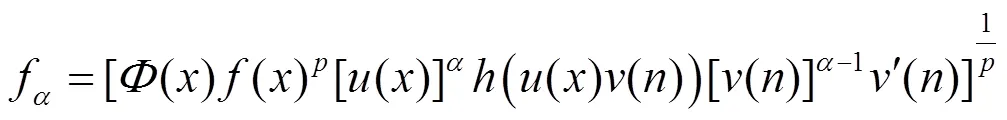
证明 由引理1和引理2, 有:

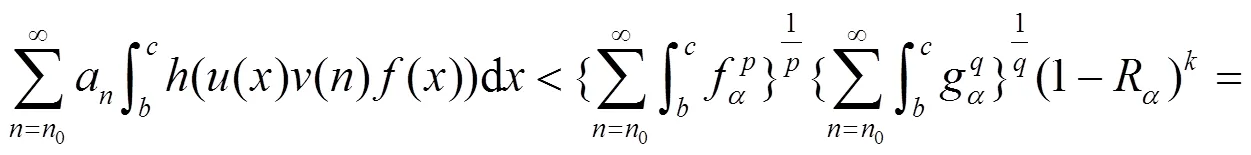
即(5)式得证.

,

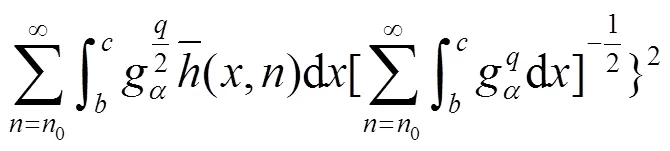
注: 式(5)即为式(2)的改进式.

[1] Yang Bicheng. A half-Discrete Hilbert-Type Inequality with a Non-Homogeneous kernel and two variables[J]. Mediterr J Math, 2012(12): 213—218.

[2] He Leping, Gao Mingzhe, Jia weijian. On a New Strengthened Hardy-Hilbert’sInequality[J]. Journal of Mathematical Research and Exposition, 2006, 26(2): 276—282.

[3] He Leping, Gao Mingzhe. A Hilbert Integral Inequality with Hurwitz Zeta Function[J]. Journal of Mathematical inequalities, 2013, 7(3): 377—387.

Improvement of half-discrete Hilbert-type inequality with non-homogeneous kernel

HE LePing, LIU Tuo

(College of Mathematics and Statistics, Jishou University, Jishou 416000, China)

Hilbert-type inequality are important in analysis and its applications. In this paper, a half-discrete Hilbert-type inequality is investigated. By using the way of weight functions and the techniuque of real analysis and a sharpening of Hölder’s inequality, some improvements of Hardy-Hilbert’s inequality are given, a few new inequalities are established.

O 178

1672-6146(2014)01-0001-03

10.3969/j.issn.1672-6146.2014.01.001

通讯作者email: jdlepinghe@163.com.

2014-01-08

国家自然科学基金资助项目(11261020)

(责任编校:刘晓霞)