纸巾包装机夹纸机构冲击强度计算

何炜平, 张 成, 张红涛



纸巾包装机夹纸机构冲击强度计算

何炜平*1, 张 成2, 张红涛2

(1. 常德烟草机械有限责任公司 总工程师办公室, 湖南 常德, 415000; 2. 湖南大学 机械与运载工程学院, 湖南 长沙, 410082)

建立某型纸巾包装机夹纸系统冲击/动态接触有限元模型, 计算了四杆机构推杆对夹纸活动板的冲击力、冲击时间, 活动板关键点时间-应力历程. 分析结果表明, 夹纸系统的最大冲击应力小于材料的许用应力, 抗冲击强度满足工作需要. 验证了纸巾包装机夹纸机构的稳定工作的条件, 并对机构的后续结构优化有一定的指导作用.

包装机; 夹纸机构; 冲击力; 抗冲击强度

夹纸机构是纸巾包装机的核心部件, 其结构性能跟整机稳定性和工作效率紧密相关, 直接影响夹纸质量. 本文所述类型包装机夹纸机构的良好结构性能主要体现在夹纸活动板的抗冲击强度上. 抗冲击强度是评价机械零件质量的重要指标, 在进行机械设计时, 抗冲击强度往往起着决定性作用[1]. 设计夹纸机构结构时, 需同时满足结构强度和机构轻量化的要求.

冲击问题随着计算科学的发展被研究者关注. 1976年, T. J. R. Hughes[2]等首先应用有限元法研究了冲击-动力接触问题. 文献[3—6]采用不同方法研究冲击-动力接触问题有限元方程, 并基于Newmark-β直接积分法对方程进行求解. 文献[7]提出了一种三维冲击-动力接触问题的有限元混合算法. 文献[8]验证了瞬态接触-冲击问题的一种基于拉格朗日乘子法的有限元公式系统及其数值求解方法. 文献[9]计算了某型包装机运行机构同步带运行时的应力分布与前15阶模态, 讨论了同步带结构的合理程度及振动情况. 文献[10]对高速包装机的椭圆齿轮做有限元分析, 得出了椭圆齿轮在静力作用下的应力分布. 近年来, 应用有限元软件对冲击问题的分析已在实际工程中有多方面的应用[11—13].

本文基于有限元软件ABAQUS建立了夹纸机构受冲击载荷时的计算模型. 基于该模型计算了与活动板冲击强度相关的冲击力、冲击应力等, 对夹纸活动板的抗冲击强度有了较深的讨论.

1 冲击问题基本方法与计算原理

夹纸机构的冲击问题集中在四杆机构的推杆对夹纸活动板的动态接触(图1). 夹纸活动板在四杆机构推杆的推动下向上运动一角位移, 在弹簧拉力的作用下和夹纸固定板把纸夹紧. 由于推杆速度较快, 且与活动板作用时间极短, 活动板会承受较大的冲击力, 有必要对活动板进行冲击强度分析.

冲击问题是复杂的非线性接触问题, 有限元接触分析建立在弹塑性理论和接触力学基础之上. 推杆对活动板的冲击是一个短暂、瞬时的动态事件, 选用ABAQUS/Explicit模块分析较合适. 刚开始接触时, 动力学平衡方程为:

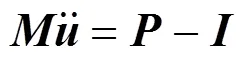
在时刻, 加速度为:

任何节点的加速度都取决于节点质量和作用在节点上的合力. 对加速度在时间上进行积分时, ABAQUS/Explicit采用显式中心差分法. 在计算速度的变化时假定加速度为常数,时刻的速度为:

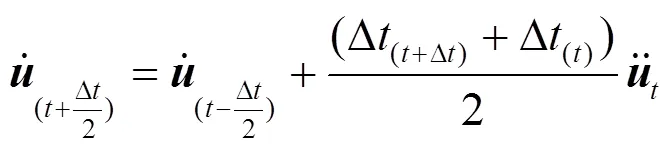
将速度对时间积分即得到节点的位移:

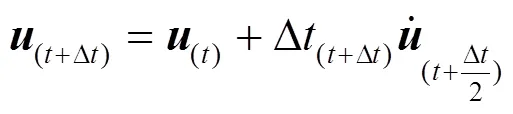
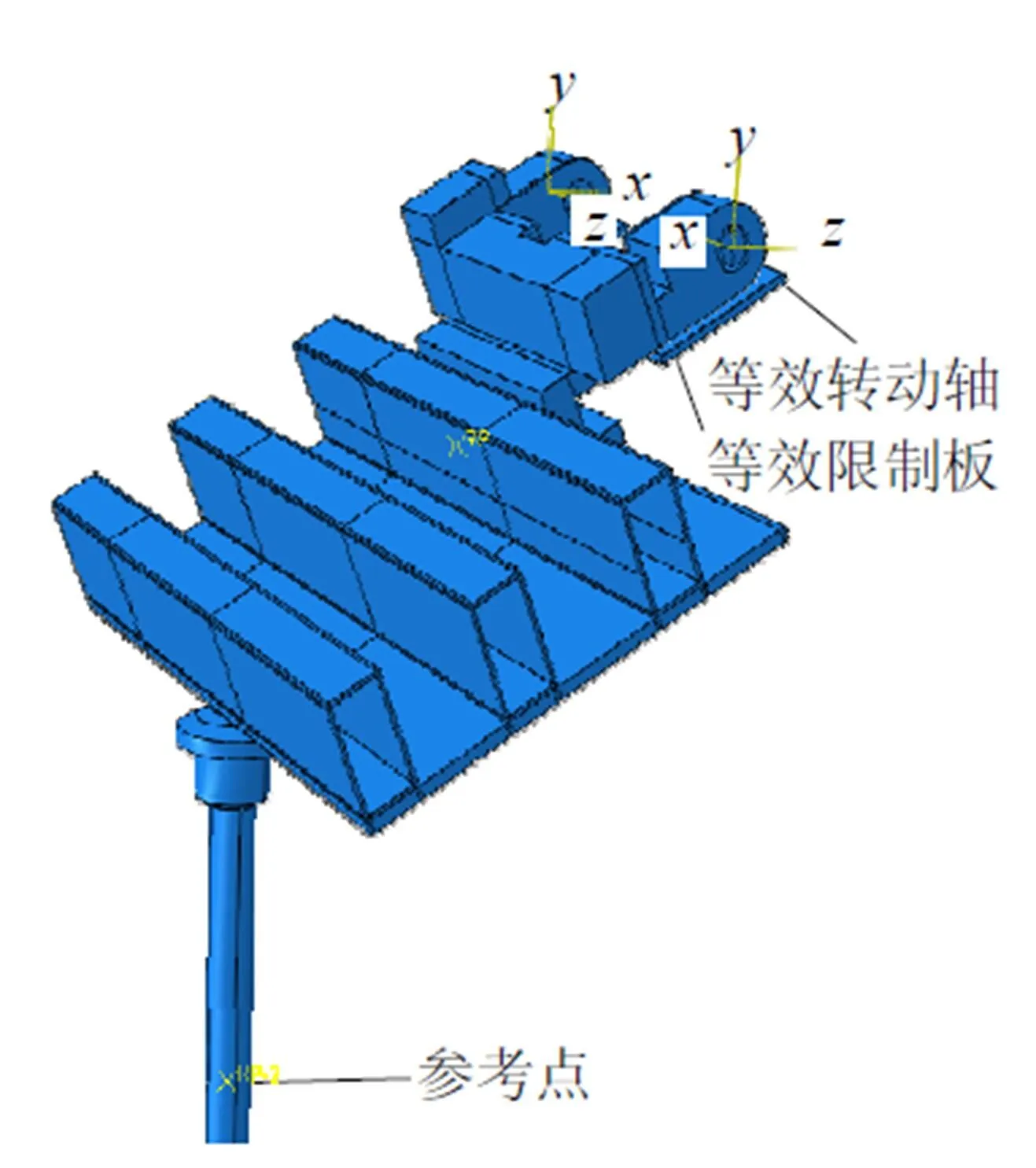
图2 推杆对底板的冲击示意图

2 冲击有限元模型的建立

为节省计算耗时, 对图1的结构进行适当简化, 建立有限元模型. 推杆的运动规律由曲柄推杆四杆机构确定, 四杆机构的运动可只考虑推杆的运动, 给出推杆的速度曲线即可.

2.1 约束关系

为保证活动板初始位置的平衡, 和实际边界条件一致, 给活动板建立了等效限制板. 等效限制板施加全约束, 推杆对活动板的冲击有限元模型约束可简化(图2).

在图2中, 去掉推杆四杆机构中的曲柄和连杆, 只保留推杆和触头, 触头和推杆以绑定约束固定在一起, 为触头和推杆建立运动参考点, 参考点为推杆和触头的质心, 把触头和参考点以运动耦合的方式约束起来, 推杆运动的速度函数施加给参考点即可用来控制推杆的运动. 给活动板建立与实际情况一致的等效转动轴. 转动轴和活动板之间以连接单元(hinge)连接(图3), 它和实际铰链连接一致. 等效转动轴全约束, hinge连接单元限制了活动板5个方向的自由度, 如此即可以实现活动板的转动.

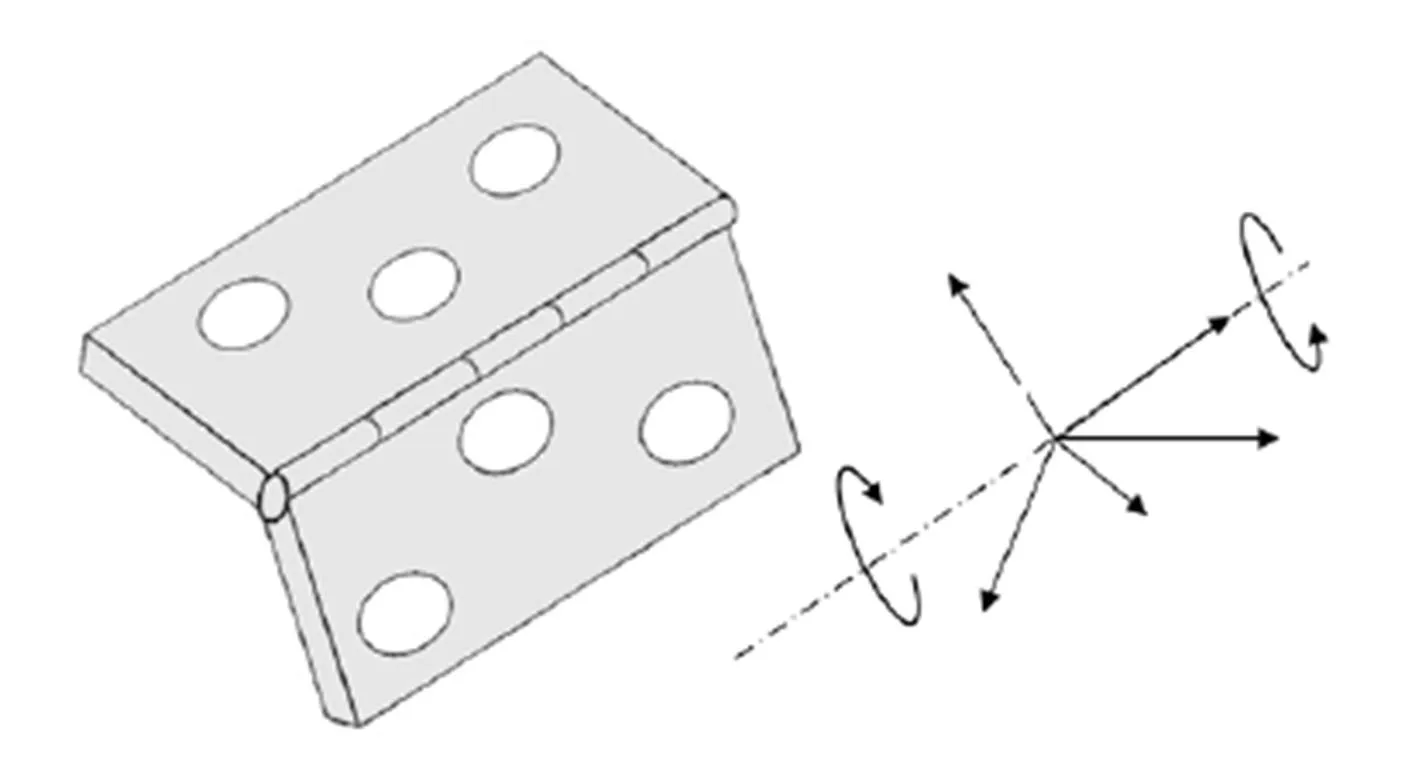
图3 hinge连接单元

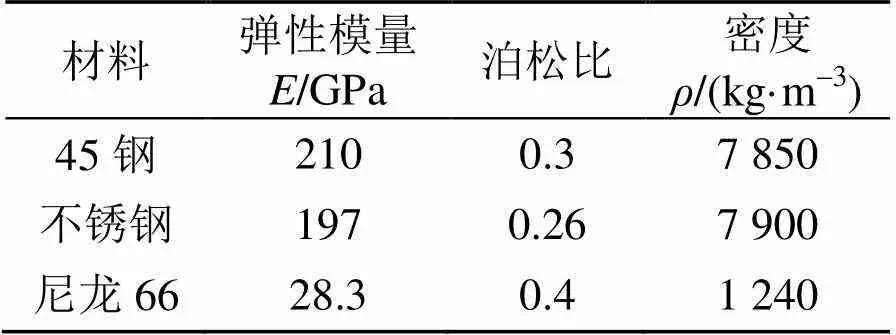
表1 材料参数

2.2 材料参数

抓纸系统结构材料主要有3种: 底板与槽的材料为不锈钢, 推杆触头材料为尼龙66, 其它零件材料为45钢, 各种材料参数见表1.

2.3 有限元模型

活动板与其它零件之间的铰接位置远离冲击区域, 可去掉对结果影响很小的连接孔, 把活动板和与之固连的零件整体建模并划分网格(采用六面体单元C3D8R). 推杆和触头形状较规则, 剖分后可直接划分出形状较理想的网格. 按照正确位置装配各个零件. 推杆对活动板的冲击力取决于接触时的冲击速度, 与推杆之前的运动无关, 据此把推杆装配在离活动板很近的位置, 在参考点上施加即将接触时推杆的速度, 即减少计算时间, 又保证结果的合理性. 按照实际约束情况, 给各个零件定义约束, 等效限位板和转动轴全约束, 推杆约束除运动方向外的其他5自由度, 运动方向施加速度边界条件, 即冲击速度(图4).

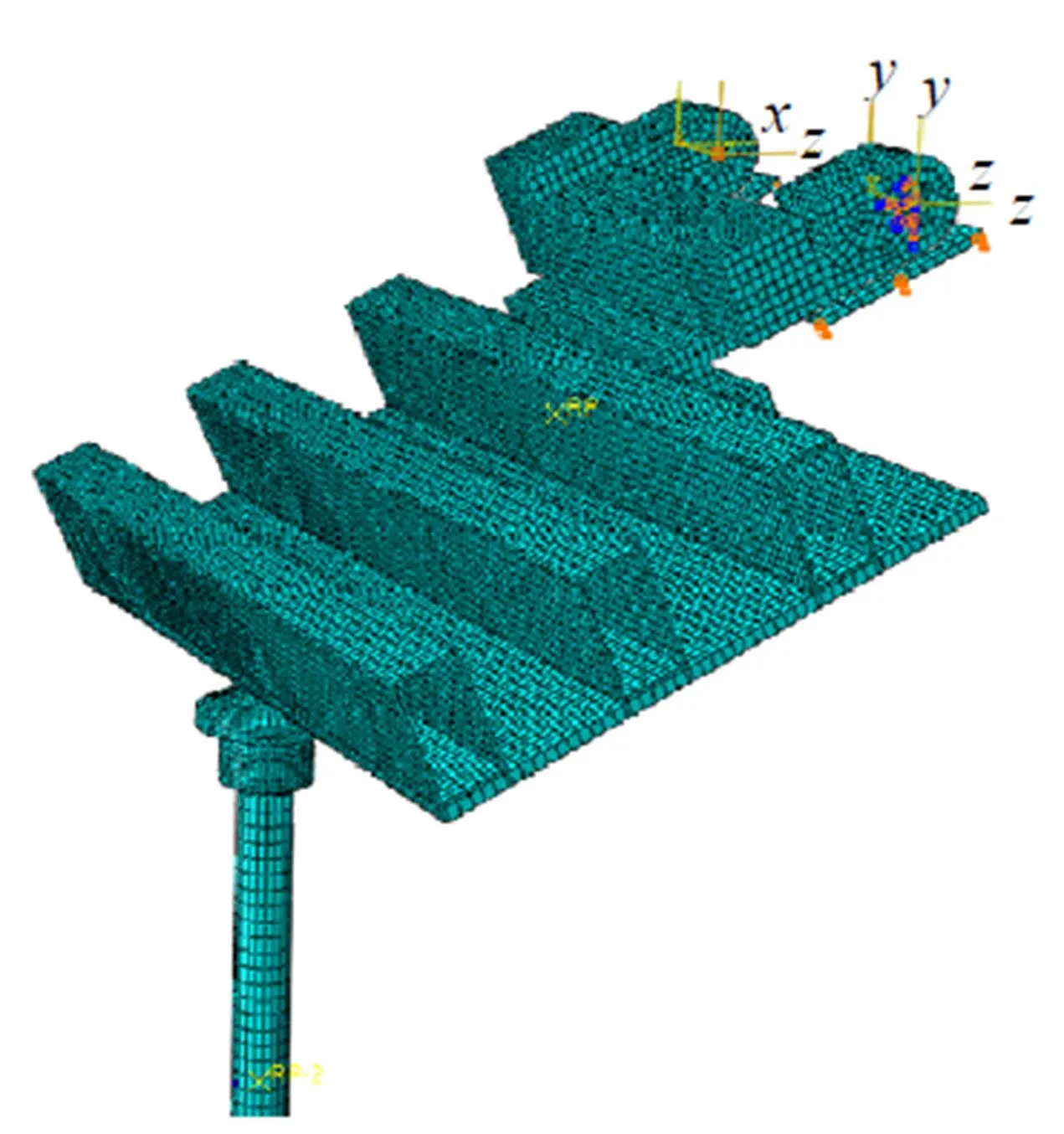
图4 整体有限元计算模型

3 计算结果分析

在满足工作条件下, 推杆的速度越小, 冲击越小. 受推杆四杆机构结构样式、安装等因素制约, 推杆的速度在400 mm/s以上才能够推起活动板. 为保证夹纸过程稳定, 推杆速度边界条件设为500 mm/s.

图5 推杆触头与活动板间的接触力变化

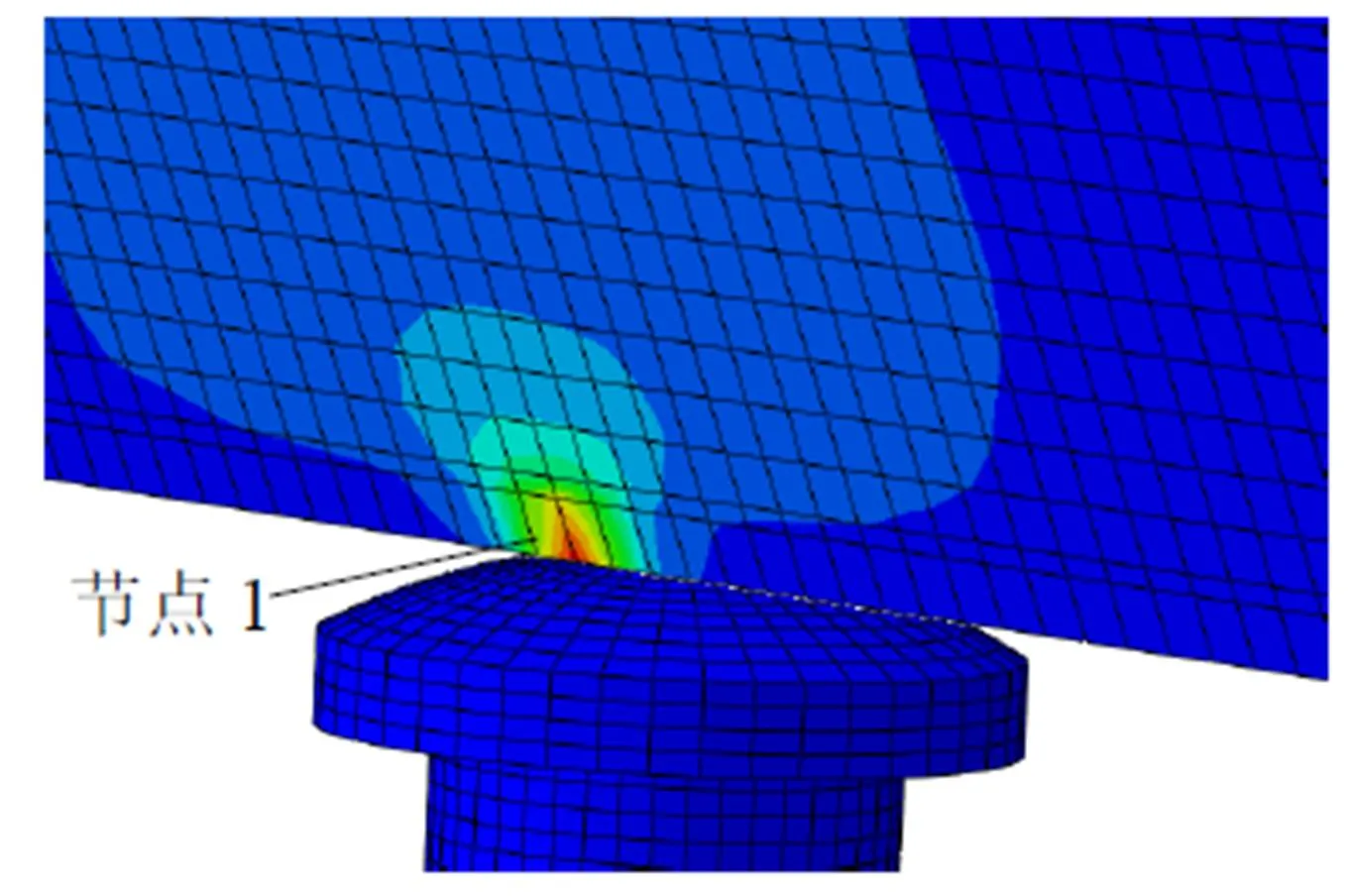
图6 活动板冲击位置应力云图

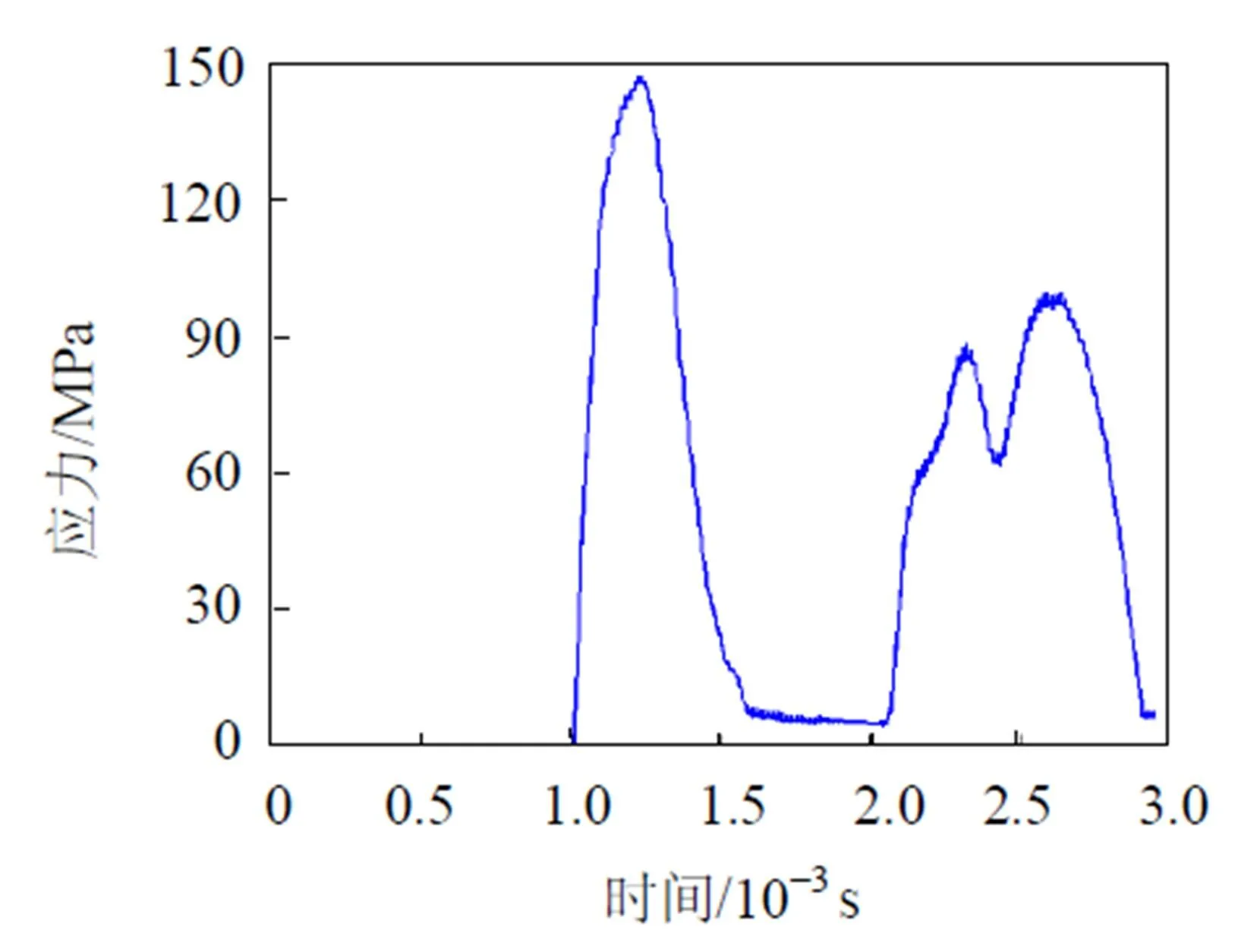
图7 节点1应力曲线

由图5可知: 触头与活动板冲击后, 活动板获得一个向上的冲量=·Δ, 其大小为图5中第1段曲线与坐标轴所形成区域面积, 冲量转化为活动板上升所需的动量, 由于作用时间极短, 活动板会加速上升, 与触头有短暂的分离, 在重力矩的作用下会再次与推杆接触. 分离时间约为0.5 ms, 第2次接触的冲击力减小, 相应的冲量也减小. 最大应力位于触头与活动板接触位置的节点1, 以该点为中心向四周逐渐减小(图6). 对比图5和图7, 节点1的应力曲线和接触力的变化曲线基本一致. 参照不锈钢-1Cr18Ni9Ti的屈服强度(≥ 200 MPa), 节点1的最大应力为145 MPa, 其冲击应力小于材料的许用应力, 满足结构的冲击强度要求.

4 结论

利用有限元软件ABAQUS, 对夹纸机构进行了接触冲击分析. 建立了实际工况下夹纸机构的瞬态冲击有限元模型. 计算了推杆与活动板的冲击力、冲击时间以及活动板动态应力,得出了冲击点随时间变化的应力曲线. 计算表明, 冲击区域最大冲击应力小于材料的许用应力, 夹纸活动板抗冲击强度满足要求. 计算结果对夹纸机构后续的结构优化也具有一定的参考价值.

[1] 田相克. 产品抗冲击强度分析的有限元建模及落球冲击试验仿真[J]. 机械强度, 2010, 32(6): 1022—1025.

[2] Thomas J R, Hughes. A finite element for a class of contact impact problems [J]. Comp Meth Appl Meth Engng, 1976, 8: 249—276.

[3] Chaudary A B, Bathe K J. A solution method for static and dynamic analysis of three-dimensional contact problems with friction [J]. Comp and Struc, 1986, 24(6): 855—873.

[4] Mahmoud F F, Hassan M M, Salamon N J.Dynamic contact of deformable bodies [J]. Comp and Struc 1990, 26(l): 169—181.

[5] Kanto Y, Yakawa G. A dynamic contact buckling analysis by the penalty finite element method [J]. Int J Num Meth Engng, 1990, 29: 755—774.

[6] Taylor R L, Papadopoulos P. On a finite element method for dynamic contact/impact problems [J]. Int J Number Meth Engng, 1993, 36(12): 2123—2140.

[7] 欧垣安, 李润方, 龚剑霞. 三维冲击-动力接触问题的有限元混合算法[J]. 重庆大学学报, 1994, 17(2): 52—57.

[8] 李俊, 金咸定, 李维扬. 瞬态接触-冲击问题的有限元分析[J]. 上海交通大学学报, 1997, 31(11): 78—81.

[9] 汤庆华, 殷国富, 徐长学, 等. 包装机运行机构同步带轮的结构和模态分析研究[J]. 新技术新工艺, 2008, 12: 68—70.

[10] 黄志东, 韩杨, 王宇. 高速包装机椭圆齿轮的有限元分析[J]. 辽宁科技学院学报, 2011, 13(1): 18—24.

[11] 曾祥国, 刘世品, 李琼阳, 等. 冲击载荷下材料动态断裂参数的有限元计算[J]. 四川大学学报, 2007, 39(6): 1—6.

[12] 江德增, 黄小清, 汤立群. 冲击荷载下半刚性护栏的非线性有限元分析[J]. 华南理工大学学报, 2003, 31(3): 64—67.

[13] 汪玉, 赵建华, 杜俭业, 等. 基于多体动力学有限元计算的一种舰用柴油机抗冲击性能仿真[J]. 振动与冲击, 2009, 28(11): 87—90.

Impact strength analysis of a paper tissue packing machine

HE WeiPing1, ZHANG Cheng2, ZHANG HongTao2

(1. Changde Tobacco Machinery Co., LTD, Changde 415000, China; 2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)

An impact/dynamic contact finite element model of a paper tissue packing machine clipped system is built. Impact force and impact time between four-bar linkage putter and moving clipped paper board are calculated. Meanwhile, the time–stress history of moving clipped paper board key point is obtained. Analysis results show that the maximum impact stress of clipped paper system is less than the allowable stress of material. Impact strength can meet the needs of working environment. This study verifies working conditions of the paper tissue packing machine clipped system is stable, it also plays a certain guiding role of the optimization of mechanism design.

packing machine; clipped paper system; impact force; impact strength

10.3969/j.issn.1672-6146.2014.04.013

TH 123+.3

1672-6146(2014)04-0052-03

email: hewp@ccdtm.com.

2014-02-05

http://www.cnki.net/kcms/doi/10.3969/j.issn.1672-6146.2014.03.0.html

(责任编校:刘刚毅)