柴河流域土壤全氮克里格插值的参数优选①

王 泉 吴献花

(1.玉溪师范学院 玉溪高原湖泊生态环境研究中心,云南 玉溪 653100)

柴河流域土壤全氮克里格插值的参数优选①

王 泉 吴献花②

(1.玉溪师范学院 玉溪高原湖泊生态环境研究中心,云南 玉溪 653100)

柴河流域;克里格插值;空间数据;全氮测定;参数优选

利用普通克里格方法对柴河流域50个土壤采样点2011年测定的全氮含量平均值进行插值分析,探讨变异函数模型的选择和模型参数的设置对插值精度的影响.结果表明:最优半变异函数模型为指数模型,最优插值参数为块金值0.019 6,偏基台值0.239 24,变异方向角度75°.应用上述优选的参数对柴河流域土壤全氮含量进行空间插值,得到了高精确度的插值结果.

为了防治小流域非点源污染,需要充分了解土壤养分空间变异特征[3].但实际工作中布设采样点对研究区域土壤特征进行监测只能得到采样点处的土壤特征值,不可能实现空间数据连续化.

空间插值法是通过离散的样本数据来预测未知空间数据的方法,实现了空间数据的连续化.地统计方法可以计算插值误差,并以此为依据,作为提高插值精度的参考[4].克里格插值法是应用最为广泛的地统计学方法,其变异函数模型的选择和相关参数的设置对插值的效果影响很大.目前国内外相关研究主要是针对不同的插值方法进行比较[5～11],且研究对象主要是针对县域尺度、市域尺度等以行政区划为特征[12,13],却少见针对流域的土壤空间插值研究,对于参数设置和变异函数模型的选择的研究也较少.

本研究利用普通克里格方法对滇池南部的柴河流域内50个采样点的土壤全氮含量2011年的测定数据进行插值分析.使用交叉验证的方法,优选变异函数模型及其相关参数,为该小流域控制农业非点源污染,减少施肥,实施精准农业提供参考数据,同时也希望其能为类似的研究和应用提供相应的参考和借鉴.

1 数据来源及研究方法

1.1 研究区概况

研究区域位于滇池流域的南部,地理坐标在东经102°36′～102°43′、北纬24°28′～24°43′之间,总面积为193.6 km2.年均降水量900.7 mm.土地利用类型主要是耕地,以旱地为主,主要种植玉米、蔬菜、花卉等经济作物.流域内土壤以砂岩、砾岩发育的红壤为主,局部有黄棕壤分布.

1.2 土壤采样与分析

课题组成员于2011年1月至12月,每月采样1次,在研究区内按照2 km×2 km的网格,采用MAGELLAN eXplorist 500 GPS定位布设50个采样点.采用凯氏蒸馏法测定土壤全氮[1].将每个土壤样品2011年1月至12月的全氮测定数据的平均值作为该采样点2011年的年平均值,并将其作为本研究分析的原始数据.

1.3 克里格插值方法的理论基础

空间数据探索分析(Exploratory Spatial Data Analysis,ESDA)是用来估计误差方差或半方差的工具,其目标是要建立半方差与点对间空间距离的关系,即变异函数[13].本研究使用基于ARCGIS9.3的Geostatistical Analyst模块提供的ESDA工具对土壤全氮数据进行探测和检验,这些工具包括用于检验数据正态分布的直方图工具和趋势面分析工具,并从圆形模型、球形模型、指数模型和高斯模型中优选出最适合的模型来进行插值.

2 结果与分析

2.1 正态检验及空间趋势面分析

柴河流域土壤全氮2011年的平均值(mean)为1.130 9,中数(median)为1.066 3,这两个值较为接近,表明土壤全氮的数据为正态分布.

趋势属于表面的非随机成分,克里格插值的基础是数据必须为随机变量.趋势能够用数学公式来表达,与表示这些趋势的数学公式相比,实际的趋势往往并没有这么平滑.如果用数学公式不能完美的表达实际的趋势面,可以剔除趋势,并继续分析,用模型计算其余的数据.通过空间趋势面分析发现,本研究的数据存在空间趋势.因此,在插值前先经过趋势剔除,由于是二阶多项式趋势,在趋势剔除选项里面选择second.

2.2 半变异函数模型的选择

为了提高克里格插值的精度,通过交叉检验的方法,从常用的四个变异函数模型中,选出精度最好的模型.附表为四种常用模型的交叉检验结果,表中预测误差均值(ME)越接近0,标准均方根预测误差(RMSS)越接近1时,模拟的精度越高[13].由附表可见指数模型的RMSS为1.057,在四种模型中最接近于1,ME为0.019 35,在四种模型中最接近于0.故可选择指数模型作为柴河流域土壤全氮2011年平均值克里格插值的理论模型.

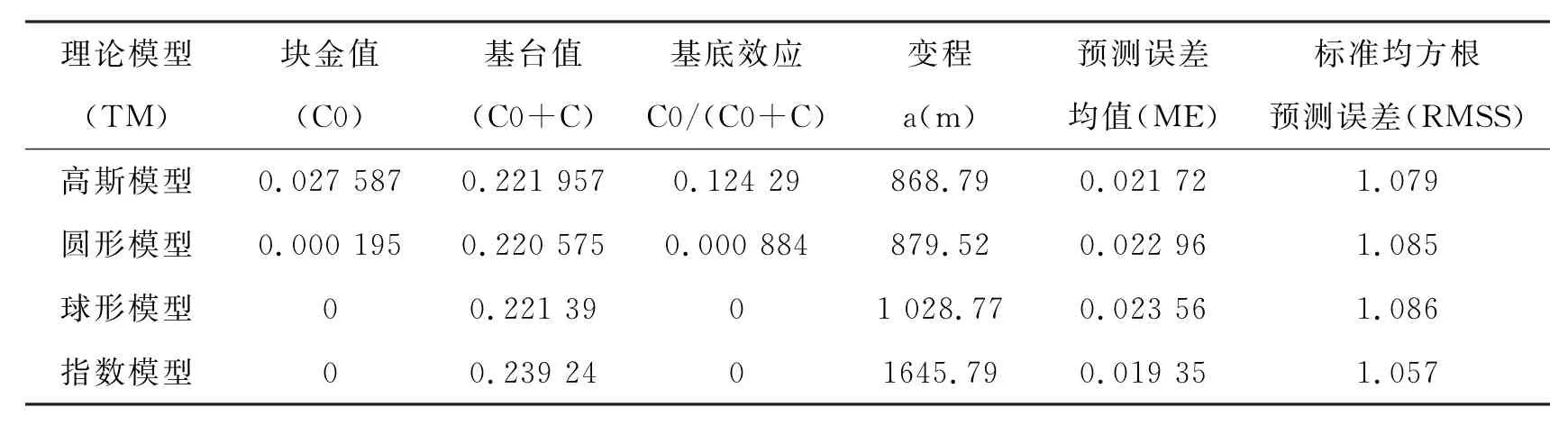
附表 不同模型的交叉检验

2.3 半变异函数模型参数设定

半变异函数的主要参数为块金值和基台值.本研究在指数模型中通过改变这两个参数的值,然后进行交叉检验分析,得到最优的取值.图1表明,块金值设置为0时,随着偏基台值的增大,RMSS逐渐降低, ME先增大后降低,最佳的偏基台值选择为0.239 24,此时RMSS为1.057,ME为0.030 507.进一步将偏基台值设置为0.239 24,随着块金值的增大,RMSS和ME均逐渐减小,在块金值为0.019 6时,RMSS为1,ME为0.016 48.在模型优选的基础上,进行块金值和偏基台值参数的优选,预测误差进一步降低了.

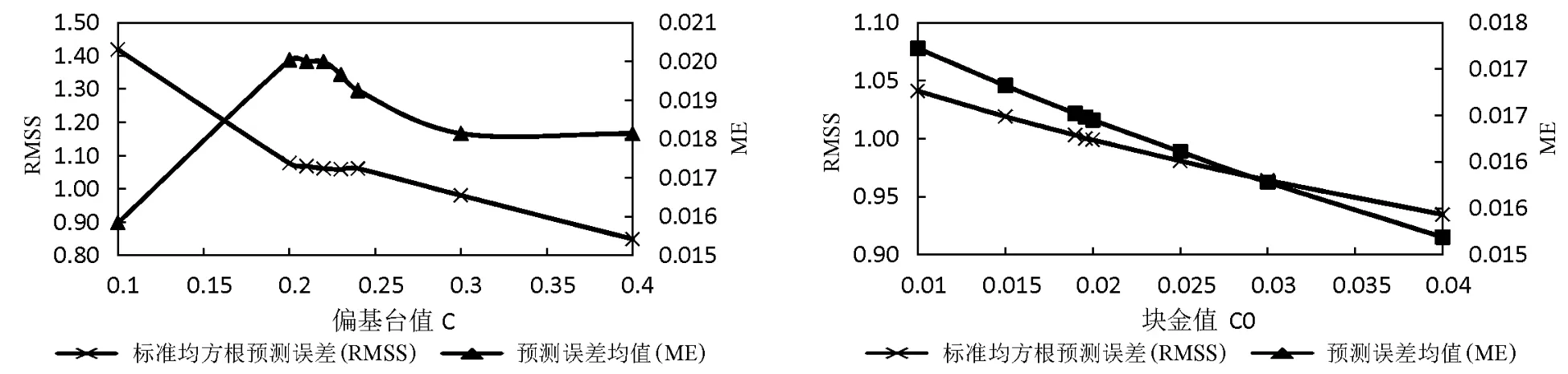
图1 不同的块金值和偏基台值的交叉检验

2.4 各向异性分析

半变异函数不仅与距离h有关,还与方向θ有关,变异函数在不同的角度上如果变程相等,则为各项同性,如果不等,则说明变异函数是各向异性的[14].图2表示了选择不同角度时的交叉检验结果,当搜索方向设定为75°时,ME为-0.001 17, RMSS为1.002,因此,变异函数在75°时模拟精度最高.

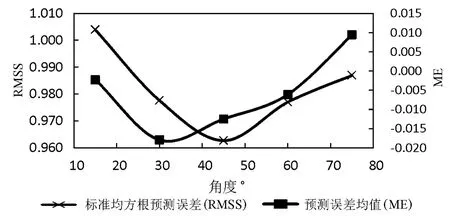
图2 各向异性的交叉检验

3 结 论

本研究利用普通克里格方法对柴河流域50个土壤采样点2011年测定的全氮含量平均值进行插值分析,探讨变异函数模型的选择和模型参数的设置对插值精度的影响.首先根据直方图工具分析数据为正态分布,确定数据可以使用普通克里格方法插值,然后探测了数据的全局趋势,发现数据存在二阶多项式的空间趋势,并对趋势进行剔除.其次,采用交叉验证的方法,判断出指数模型的拟合效果最优,在优选模型的基础上对变异函数的块金值、基台值和空间变异的方向进行优选.最终选取偏基台值为0.239 24,块金值为0.019 6,变异方向角度为75°为最优插值参数.

使用上述最优模型和参数对柴河流域2011年土壤全氮含量进行插值,其预测误差均值(ME)为-0.001 17,其标准均方根预测误差(RMSS)为1.002.上述研究表明,通过利用交叉检验分析选择最适合的半变异函数模型及其参数,可以有效的提高普通克里格插值的精度,进而较好地为流域水质改善,实施精准农业,减少施肥,控制农业非点源污染等实践服务.

[1]李海东,张波,沈渭寿,等.苏南山丘区小流域土壤养分特性空间分布[J].长江流域资源与环境,2009,18(9):831-836.

[2]季青,余明.基于协同克里格插值法的年均温空间插值的参数选择研究[J].首都师范大学学报:自然科学版,2010,31(4):81-87.

[3]常文渊,戴新刚,陈洪武.地质统计学在气象要素场插值的实例研究[J].地球物理学报,2004,47(6):982-990.

[4]Zimmerman D,Pavlik C,Ruggles A,et al.An experimental comparison of ordinary and universal kriging and inverse distance weighting[J].Mathematical Geology,1999,31(4):375-390.

[5]Price D T,Mc Kenney D W,Nalder I A,et al.A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data[J].Agriculture Forest Meteorology,2000,101(2-3):81-94.

[6]林忠辉,莫兴国,李宏轩,等.中国陆地区域气象要素的空间插值[J].地理学报,2002,57(1):47-56.

[7]冯锦明,赵天保,张英娟.基于台站降水资料对不同空间插值方法的比较[J].气候与环境研究,2004,9(2):261-277.

[8]刘胤雯,赖格英,陈元增,等.梅江河流域年均降水量空间插值方法研究[J].亚热带资源与环境学报,2007,2(3):29-34.

[9]吴文玉,马晓群.基于GIS的安徽省气温数据栅格化方法研究[J].中国农学通报,2009,25(2):263-267.

[10]王波,毛任钊,曹健,等.海河低平原区农田重金属含量的空间变异性——以河北省肥乡县为例[J].生态学报, 2006,26(12):4082-4090.

[11]刘勇,张红,尹京苑.汾河太原段土壤中Hg、Cr空间分布与污染评价[J].农业工程学报,2008,24(5):57-60.

[12]徐理超,李艳霞,苏秋红,等.阜新市农田土壤重金属含量及其分布特征[J].应用生态学报,2007,18(7):1510-1517.

[13]候景儒.实用地质统计学[M].北京:地质出版社,1998:31-73.

A Study on Parameters Setting of Ordinary Kriging Interpolation to Total Soil Nitrogen Concentration in Chaihe River Basin

Wang Quan WU Xianhua
(Yuxi Research Center for Eco-environmental Sciences,Yuxi Normal University,Yunnan 653100,China)

Chaihe River Basin;Kriging;Exploratory Spatial Data Analysis(ESDA);semivariogram model;optimal parameters

The ordinary Kriging is used to interpolate a surface of 50 soil nitrogen concentrations which were collected and analyzed in 2011 in Chaihe River Basin.Under the support of ArcGIS software and optimal theoretical model in the process of interpolation,optimal parameters for a semivariogram model are calculated such as best nugget,partial sill and directional influences with the cross-validation.The results show that the optimal theoretical model is exponential semivariogram model.The best nugget,the partial sill and the directional influences are 0.019 6,0.239 24 and 75°respectively.Finally,the optimal interpolation results are acquired by the optimal parameters based on analysis of soil nitrogen concentrations of spatial interpolation in Chaihe River Basin.

X522

A

1009-9506(2014)08-0028-04

2014年4月2日

王 泉,研究方向:湖泊水环境调查及环境数值模拟.

国家水体污染控制与治理科技重大专项,编号:2009ZX07102.

②通信作者:吴献花,教授,研究方向:湖泊生态修复.Email:xhw105@163.com.