基于正弦/直线过载的惯性测量组合动态误差标定系统

林红斌，周建平，王 妍

（1.国防科学技术大学航天科学与工程学院，长沙410073；2.中国载人航天工程办公室，北京100029；3.中国人民解放军第二炮兵装备研究院，北京100094）

·工程技术·

基于正弦/直线过载的惯性测量组合动态误差标定系统

林红斌1，3，周建平2，王 妍3

（1.国防科学技术大学航天科学与工程学院，长沙410073；2.中国载人航天工程办公室，北京100029；3.中国人民解放军第二炮兵装备研究院，北京100094）

为解决航天器惯性测量组合与过载相关的动态误差难以在地面精确标定的问题，提出并构建了一种基于正弦直线过载的惯性测量组合动态误差试验系统。利用该系统提供过载的正弦特性和直线往复运动的周期特性，结合惯性测量组合在正/负半周期内的脉冲输出，标定惯性测量组合动态误差。试验结果表明，采用该系统标定的惯性测量组合动态误差重复性、一致性好，是惯性测量组合动态误差的地面精确标定的一种有效手段。

惯性导航；动态误差标定；正弦直线过载；惯性测量组合

1 引言

惯性测量组合（以下简称惯组）是航天器惯性导航系统的重要组成部分，其性能的好坏直接影响航天器的入轨和落点控制精度，随着控制精度要求的不断提高，对惯组的测试技术越来越引起人们的重视。

惯组中陀螺、加速度计的输出不仅与角速度、角加速度有关，而且与线加速度有关。目前，高精度转台完全能够复现航天器绕质心运动的角速度、角加速度，对该状态下惯组的性能作出科学的评价。而线加速度下性能测试通常采用重力场静态位置翻滚测试、精密离心测试、电模拟测试、冲击振动试验、火箭撬等方法，目前这些方法用于惯组动态误差标定存在局限性[1-5]：

1）重力场静态位置翻滚测试

该方法是在±1 g以内通过标定惯组的误差系数来代替整个量程内的参数，而航天器飞行最大加速度甚至可以达到几十个g，标定与使用条件不一致。

2）精密离心测试

该方法需要两次安装来实现正向、负向加速度，给标定奇异二阶非线性系数带来系统误差。且大过载环境时转速过大，可能超出陀螺测量范围，无法测试陀螺相关误差项。

3）电模拟法

该方法只能考察惯性器件力矩器及伺服回路功能，不能真实地模拟惯性力作用效果，而惯性器件结构弊病在大加速度输入条件所引起的输入误差不容易发现。

4）冲击振动试验

该方法采用环境试验用线振动台，精度低、寄生振动大，当工作频率较低时，不能实现大的过载，且漏磁严重，无法用来测试惯组的动态参数，只用于惯组可靠性筛选。

5）火箭撬或飞行试验

为模拟航天器飞行状态，国内外采用了火箭撬的形式实现直线过载[1，5]。火箭撬试验技术有轨道占地面积巨大、试验周期长、试验费用极其昂贵、外测手段难以保障等缺点，难以用于惯组动态误差的标定。而飞行试验则由于费用更加昂贵，试验数量极少，提供的数据不充足，不能充分指导惯组的生产。

国内外对于捷联惯组超过1 g条件下的精确标定尚无理想的测试方法。针对目前惯组线加速度测试技术的局限性，本文提出一种利用直线过载试验台分离惯导动态误差的新方法，构建了试验系统，完成对惯组动态误差的标定。该系统的建立，为完善惯性仪表动态标定研究，提高惯组在低频、大过载等条件下的精度，提供了可行的技术途径。

2 正弦直线过载试验系统原理

2.1 正弦机构工作原理

正弦直线过载试验系统的工作原理如图1所示。

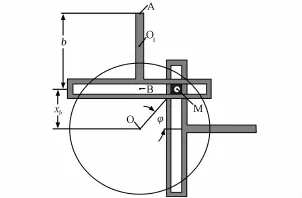
图1 正弦机构示意图Fig.1 Frame of sine institution

当曲柄OM自φ=φ0的位置以ω稳速转动时间t时，从动件A点运动矢量如式（1）所示。

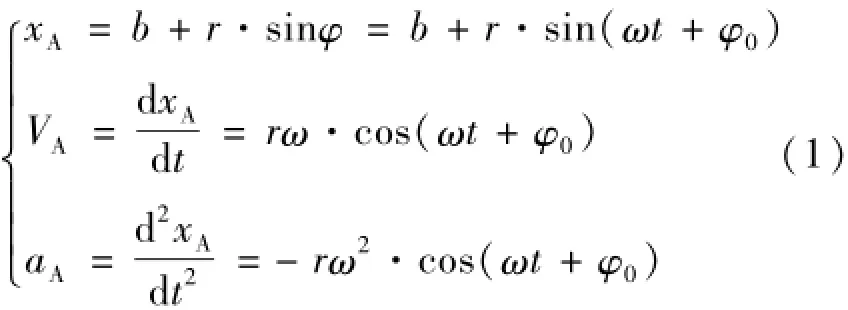
式中：r为曲柄长度，单位为m；

b为连杆长度，单位为m；

ω为曲柄角速度，单位为rad/s；

φ0为初相位，单位为rad；

xA为A点（从动件）与旋转中心距离，单位为m；VA为A点（从动件）瞬时速度，单位为m/s；aA为A点（从动件）瞬时加速度，单位为m/s2。从加速度公式可以看出，A点输出加速度为简谐运动。

2.2 动能传递机构的能量传递原理

滑台动能可写为式（2）。

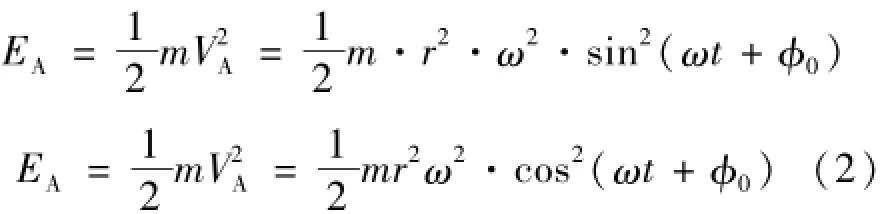
由于滑台和惯组质量大，其动能亦很大且变化剧烈，如果循环不断地刹车、加速驱动，会造成能量的极大浪费。需要采用滑块间动能传递技术，达到动能传递的目的，整个系统就可以大幅降低能耗。

将飞轮两边附带两个等质量、相位差90°的滑块在等长（振幅相同）的导轨中运动，如图2（a）所示，滑块动能分别写成式（3）。

飞轮按顺时针方向旋转，当滑块A、B处于如图2（b）所示的位置时，相位差90°，此时，滑块A在水平方向的动能最大，即承载的惯组滑台动能最大；滑块在B水平方向的动能为零，即承载的配重滑台动能为零。

飞轮继续旋转，滑块A的动能不断减小，会转变到滑块B的动能，当旋转至图2（c）所示位置时，滑块A、滑块B的动能相等，值为最大动能一半。

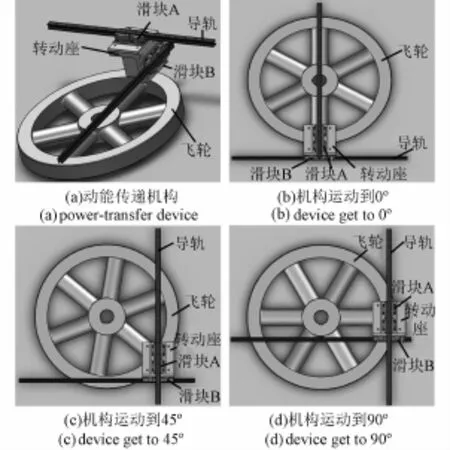
图2 动能传递机构示意图Fig.2 Fram e of pow er-transfer device

当旋转至图2（d）位置时，滑块A在水平方向的动能为零，承载的惯组滑台动能为零；滑块在B水平方向的动能最大，承载的配重滑台动能最大。

在不计摩擦、安装误差的情况下，当惯组达到要求的速度、加速度要求时，可以实现惯组负载滑台和配重滑台间的动能传递，不需电机驱动。在有摩擦、安装误差条件下，电机只需提供动力克服摩擦及微小的能量波动即可。

3 试验系统的实现

正弦直线过载试验系统主要包括试验台、控制柜、测试柜三个分系统。

试验台主要作用是将电能转变为机械能，将同步电机的旋转运动转变为工作滑台的高精度直线往复运动，并使有效载荷（惯组）随工作滑台一起处于正弦加速直线运动状态，为测试柜采集大过载环境下惯组数据提供基本条件。试验台的主体结构和内部结构见图3、图4，主要包括：

1）交流同步电机、直角型齿轮减速机、同步带（动力驱动机构）：交流同步电机加直角型齿轮减速机提供原动力，使飞轮做旋转运动；

2）飞轮、直线运动导轨（机械传动机构）：通过直线运动导轨将飞轮的旋转运动转变为推板的直线运动；

3）气浮导轨、推板部件、球铰机构、工作台（机械传动机构）：推板通过球铰机构推动工作台在气浮导轨上做正弦加速度直线运动；

4）光栅尺：实时测量被测件运动位置，解算得到被测件速率、加速度，用于计算惯组误差参数；

5）底座、支撑框：起支承、固定作用，电机、减速机、直线运动导轨、花岗岩平板等均安装在底座或支撑框上；

6）花岗岩平板：提供气浮导轨、上层直线运动导轨的安装面，保证惯组的测试精度；

7）电缆保护机构：将惯组的电缆固定在推板部件上，通过拖链与惯组同步运动；

8）调整垫铁：放在底座的底部，用于调整整个试验台，使其处于水平状态。

控制柜主要作用是对同步电机的转速进行闭环控制，以实现同步电机输出转速的高精度。测试柜主要作用是对惯组的输出脉冲数据和光栅尺测量的工作台位置数据分别进行采集、记录、计算、显示和保存，以供后续对动态误差进行计算时使用。

4 系统误差标定与分离方法

4.1 惯组动态误差模型

动态误差标定系统可以更真实地模拟大过载环境，产生较高的加速度输入，从而激励惯组与过载相关的误差输出。为了对惯组的动态误差进行标定，需要对其进行误差建模。以x向为例，考虑惯组正输出和负输出之间的差异，得到如式（4）所示加速度计和陀螺仪误差模型。

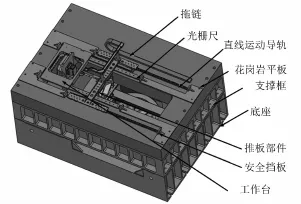
图3 试验台主体结构图Fig.3 M ain body of test bench

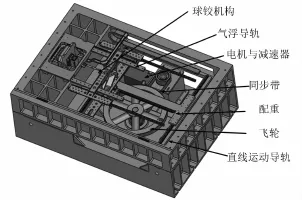
图4 试验台内部结构图Fig.4 Inside body of test bench

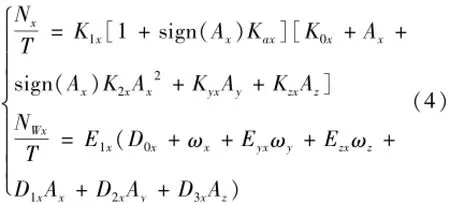
式中：Nx为x向加速度计通道输出脉冲数；

K0x为x向加速度计零偏值；

K1x为x向加速度计标度因数；

K2x为x向加速度计与x向过载二次项相关系数，为需要标定的动态误差；

Kax为x向加速度计标度因数非对称性系数，为需要标定的动态误差；

Kyx、Kzx分别为x向加速度计垂直于本体y、z向的安装误差；

Ax、Ay、Az分别为本体向过载；

NWx为x向陀螺仪通道输出脉冲数；D0x为x向陀螺仪零偏值；

E1x为x向陀螺仪标度因数；

ωx、ωy、ωz分别为本体x、y、z向角速率；

Eyx、Ezx分别为x向陀螺仪垂直于本体y、z向的安装误差；

D1x、D2x、D3x分别为x向陀螺仪受x、y、z向过载影响的一次项系数，为需要标定的动态误差。

4.2 惯组动态误差标定方法

在基于正弦直线过载试验系统标定加速度计和陀螺仪动态误差的方法，是采用光栅尺测量惯组在输入过载条件下的位移，微分得到其速度、加速度，同时采集加速度计和陀螺仪正、负通道的输出脉冲，利用常规测试的已知参数，通过下述算法，标定动态误差。

4.2.1 加速度计标度因数非对称性系数

当Ax与运动方向一致而Ay、Az与运动方向垂直时，可以省略Ay、Az的影响，考虑加速度计正负通道之间的差异，则加速度计的误差模型简化为式（5）。

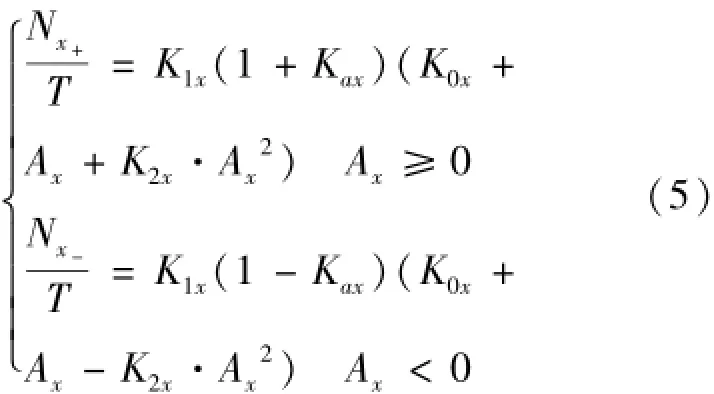
在第i个周期，分别对Ax为正和为负两个半周期内的脉冲进行累加，可得式（6）。

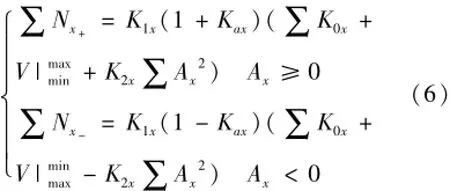
试验台滑轨零点位置设计过零判定信号，当台体通过零点时作出提示。根据正弦运动规律，当试验台正向通过零点时，速度V达到最大的Vmax，而当试验台反向通过零点时，速度V达到最小的Vmin，所以和可以分别利用试验台通过零点附近时，位置传感器信息微分得到的速度信息计算得到。则式（5）可以表示成式（7）。

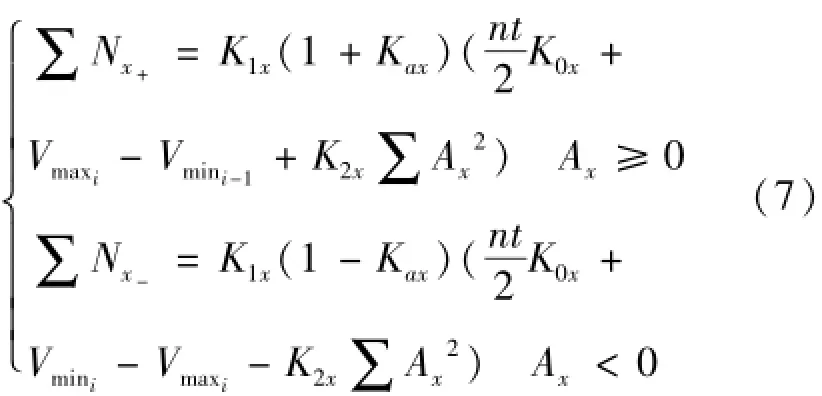
其中，n为在一个周期内采样点的个数。如果将正半周内的脉冲和加上负半周内的脉冲和，可以得到式（8）。

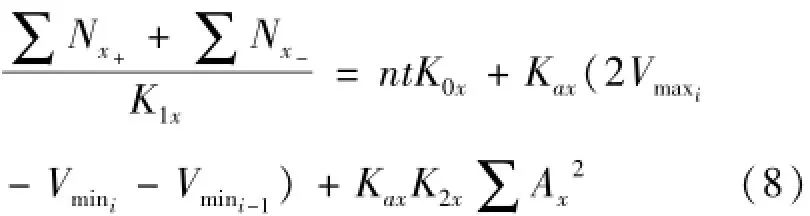
忽略小量KaxK2x，可计算出式（9）所示x轴加速度计标度因数非对称性系数Kax。

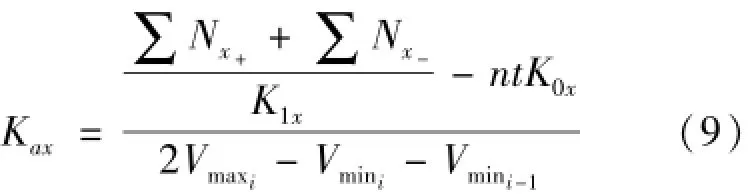
按照上述分析方法可计算y轴、z轴加速度计标度因数非对称性系数Kay、Kaz。

4.2.2 加速度计二次项相关系数

如果将正半周内的脉冲和减去负半周内的脉冲和，可以得到式（10）。

同样，忽略小量ntK0xKax，可计算出式（11）所示x轴加速度计与过载相关的二次项相关系数K2x。

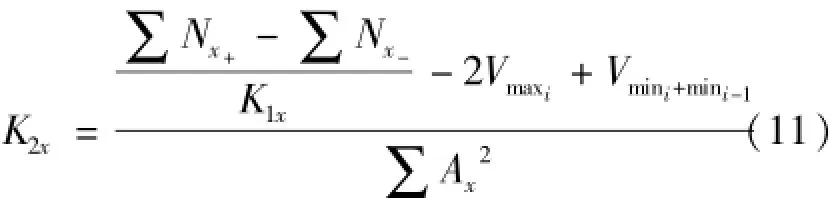
按照上述分析方法计算y轴、z轴加速度计与过载相关的二次项相关系数K2y、K2z。

4.2.3 陀螺仪一次项相关系数

正弦直线过载试验系统不提供转动环境，所有输入角速率只是地球转速的分量，为恒定量；陀螺仪误差模型中所有与转速相关参数均作为已知参数引用。当惯组x轴与试验滑台运动方向平行，y轴在竖直方向，z轴在水平面内，则Ay=1g， Az＜10-3g，忽略Az相关项，则x轴陀螺仪输出可写为式（12）。

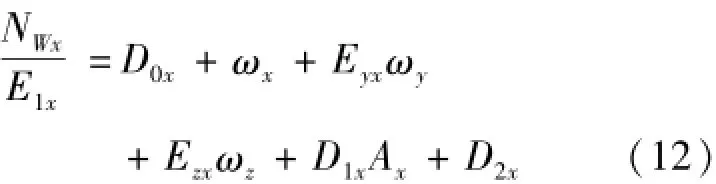
由于地球自转角速度本身已经非常小，与安装误差相乘后得到的数值会更小，可以忽略，进一步简化成式（13）。

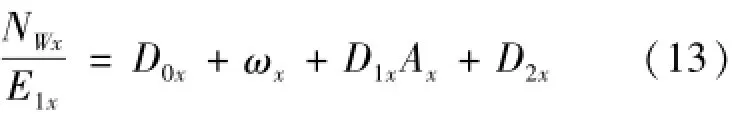
在第i个周期，分别对Ax为正和为负两个半周期内的脉冲进行累加，可得式（14）。

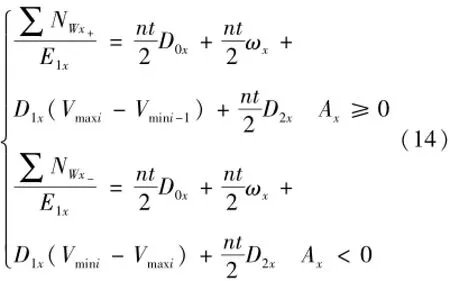
将正半周内的脉冲和减去负半周内的脉冲和，可以得到式（15）。

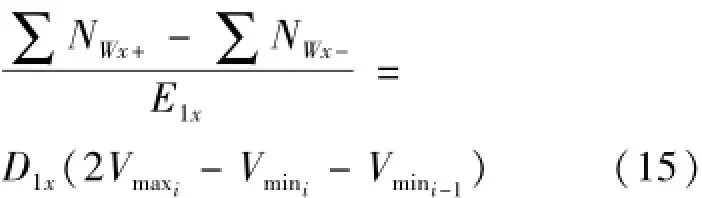
于是可以得到x轴陀螺仪与x向过载相关的一次项相关系数如式（16）。

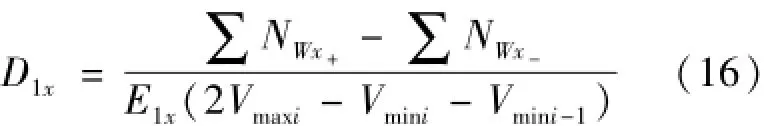
当Ay与运动方向一致而Ax、Az与运动方向垂直时，可按照上述分析方法计算x轴陀螺仪与y向过载相关的一次项系数如式（17）。

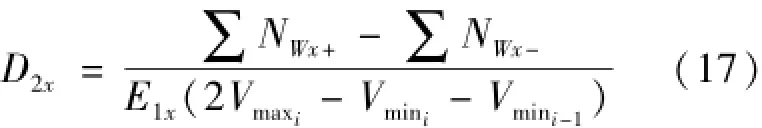
当Az与运动方向一致而Ax、Ay与运动方向垂直时，可按照上述分析方法计算x轴陀螺仪与z向过载相关的一次项系数如式（18）。

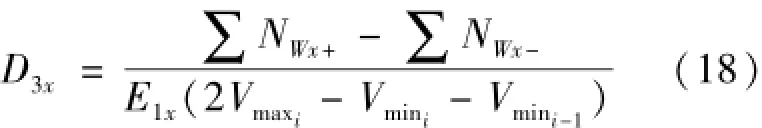
5 试验与结果分析

5.1 系统性能检验试验主要采用以下步骤检验直线过载试验系统性能：

1）在工作台上安装45 kg负载（惯组配工装），将控制柜设置为手动模式，飞轮以转速不超过18°/s运动，用激光干涉仪在工作台整个行程上取30个点，分别测量出每个点的偏角；

2）根据测量得到的位置数据以及该位置对应的偏角θ（单位为弧秒），利用作图法得到偏差最大的点，再根据公式计算得出俯仰、横摇方向的偏差；

3）对光栅尺进行位移测量，确认位置采集精度满足试验使用要求；

4）进行多次运行试验，加速度幅值分别达到1 g、2 g、3 g、4 g、5 g、6 g、7 g、8 g、9 g、10 g、11 g、12 g，记录启动时间、峰值加速运行时间和运行中情况。

5.2 惯组动态误差标定试验

1）将惯组安装在工装上，x轴与试验台运动方向平行，y轴在竖直方向，z轴在水平面内；在控制柜操作面板上设置试验加载的过载大小和试验时间；启动测试柜数据采集软件，分别采集光栅尺测量的试验台位置数据和惯组输出的脉冲数据并记录；计算x轴加速度计标度因数非对称性系数Kax，与过载相关的二次项系数K2x，陀螺仪与过载相关的一次项系数D1x、D1y、D1z。

2）改变惯组的安装方向，y轴与试验台运动方向平行，x轴在竖直方向，z轴在水平面内；重复操作1）；计算y轴加速度计标度因数非对称性系数Kay，与过载相关的二次项系数K2y。

3）改变惯组的安装方向，z轴与试验台运动方向平行，x轴在竖直方向，y轴在水平面内；重复操作1）；计算z轴加速度计标度因数非对称性系数Kaz，与过载相关的二次项系数K2z。

5.3 试验结果

5.3.1 系统性能检验试验结果

试验系统主要技术指标及满足情况见表1。

5.3.2 惯组动态误差试验结果

采用多套不同的惯组，以不同的时间间隔，利用试验系统对其动态误差进行标定，从大量的试验结果，分析加速度计和陀螺动态误差的变化规律。图5至图9为某套惯组三次实际试验结果，图中各误差单位为处理后的归一化单位。

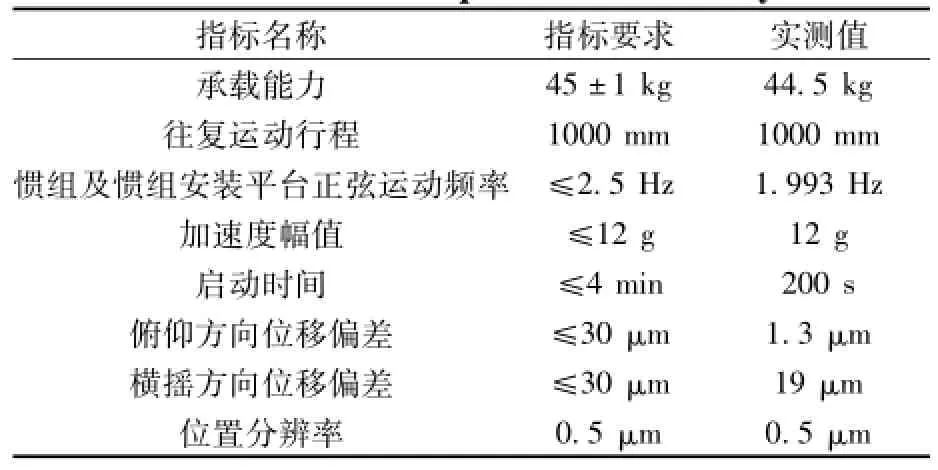
表1 试验系统实测技术指标Table 1 Technical requirements of the system

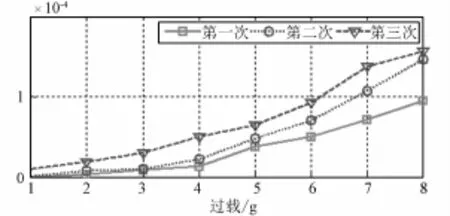
图5 x轴加速度计标度因数非对称性Kax标定结果Fig.5 Calibration result of x accelerometer scale factor asymmetry error Kax

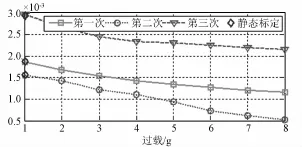
图6 x轴加速度计二次项相关系数K2x标定结果Fig.6 Calibration result of x accelerometer quadratic error coefficient related to overloading K2x

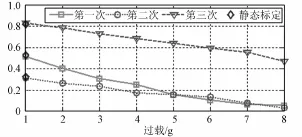
图7 x轴陀螺一次项误差系数D1x标定结果Fig.7 Calibration result of x gyro linear error coefficient D1x

通过对试验数据的分析，可得出以下结论：

1）直线过载试验系统可以提供满足惯组动态误差标定测试要求的过载环境，基于该系统的惯组动态误差标定方法能够满足惯组动态误差标定的要求；

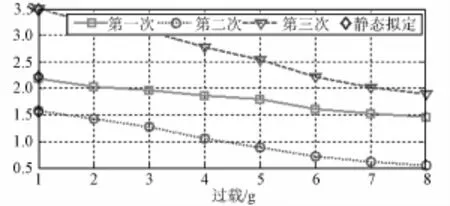
图8 y轴陀螺一次项误差系数D1y标定结果Fig.8 Calibration result of y gyro linear error coefficient D1y

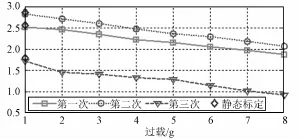
图9 z轴陀螺一次项误差系数D1z标定结果Fig.9 Calibration resu lt of z gyro linear error coefficient D1x

2）加速度计、陀螺与过载相关的动态误差在逐次通电情况下，标定结果的变化规律具有一定的重复性，且逐次通电时利用新标定系统1 g环境下的标定结果与静态多位置翻滚测试的标定结果具有良好的一致性，证明利用新研制的标定系统对加速度计和陀螺的动态误差进行地面标定的方法是正确可行的；

3）加速度计、陀螺与过载相关的动态误差在逐次通电时有一定的漂移，这与惯组各项误差逐次通电稳定性分析的结论一致，在一定程度上也可以说明该动态误差标定方法的正确性；

4）加速度计标度因数非对称性误差在一次通电情况下的标定结果具有一定的规律性，可以看出加速度计承受的过载越大，其标度因数非对称性误差越大；

5）加速度计与过载相关的二次项误差系数在一次通电情况下的标定结果具有一定的规律性，可以看出加速度计承受的过载越大，其与过载相关的二次项误差系数越小；

6）陀螺与过载相关的一次项误差系数在一次通电情况下的标定结果具有一定的规律性，可以看出陀螺承受的过载越大，其与过载相关的一次项误差系数越小。

6 结论

本文提出并构建了一种正弦直线过载试验系统作为惯组动态误差标定设备，采用十字滑块正弦能量传递机构将电机的高速旋转转换成直线往复运动，以此提供满足惯组测试要求的正弦直线过载，激励惯组与过载相关的误差输出。利用直线往复运动的周期性和惯组正/负半周期的脉冲输出，计算加速度计标度因数非对称性系数、与过载相关的二次项系数、陀螺仪与过载相关的一次项系数。试验结果表明，正弦直线过载试验系统可以满足惯组动态误差标定的要求。该试验系统的建立，为完善惯性仪表动态测试研究，提高其在低频、大过载等动态条件下的精度，提供了一种可行的技术手段。

[1] Babichenko A V，Shkred V K.Main errors of inertial navigation systems[J].Engineering Physics，2011，11：34-53.

[2] Li G，Xian Y，WangM.Dynamic separationmethod ofstrapdown inertial navigation instrument error[C]//Control and Decision Conference（CCDC），2010 Chinese.IEEE，2010：4302-4305.

[3] 王大千，张英敏.加速度计1g重力场静态翻滚测试与误差分析[J].机械与电子，2009（1）：34-36.

[4] 乔永辉，曾鸣，苏宝库.离心机旋转运动对陀螺加速度计测试精度影响研究[J].航空精密制造技术，2006，42（4）：21-24.

[5] 陈东生，魏宗康.惯性测量装置火箭橇试验模拟导弹飞行过载方法[J].导弹与航天运载技术，2009（2）：8-11.

[6] 李金河，庞勇，赵继波.火箭橇试验加载技术研究[J].弹箭与制导学报，2010（5）：137-139.

[7] 林红斌，解静，王妍.基于直线过载的惯组动态误差标定方法[J].系统工程与电子技术，2013，35（10）：2152-2157.

A Sinusoidal Linear Acceleration System for Calibration of Lnertial M easurement Unit（IMU）Dynam ic error

LIN Hongbin1，3，ZHOU Jianping2，WANG Yan3
（1.School of Aerospace and Materials Engineering，National University of Defense Technology，Changsha 410073，China；2.Chinese Manned Space Agency，Beijing 100029，China；3.Equipment Institute of the Second Artillery of PLA，Beijing 100094，China）

Aiming at the difficulty of accurate calibration for inertialmeasure unit（IMU）dynamic error on the ground，a new calibration method for IMU dynamic error based on sinusoidal linear acceleration experimentation system was proposed.An experimentation system which could supply sinusoidal linear acceleration environment tomeet the IMU test requirementswas setup.By using the sinusoidal characteristic of acceleration supplied by the new system and period characteristic of linear reciprocate，combined with IMU output pulse in half positive and minus periods，IMU dynamic error was calibrated.The experiment results indicated that the IMU dynamic error calibrated by thismethod had good repetition and consistency.So thismethod provides an effective tool for IMU dynamic error accurate calibration on the ground.

inertial navigation；dynamic error calibration；sinusoidal linear acceleration；inertial measure unit（IMU）

V44

A

1674-5825（2014）03-0189-04

2014-01-11；

2014-05-05

林红斌（1964-），男，博士研究生，研究员，研究方向为导航、制导与控制。E-mail：linhb1208@163.com