基于元胞自动机理论的公共场所人员疏散模型与仿真
谭延鹏,王志坤
(德州学院机电工程学院,山东德州253023)
公共安全是经济发展和社会稳定的基础。在进行公共设施的设计时,安全疏散性能已成为至关重要的因素。由于在引起公共安全问题的诸多因素中火灾发生的较为频繁,因此对公共场所发生火灾时人员疏散的建模与仿真的意义更大。
1 元胞自动机模型理论及建模
1.1 理论模型
元胞自动机是一种模拟人员疏散过程的模型,它由一个元胞空间和定义在该空间的变换函数所组成,可以用一个四元组表示。

式(1)代表一个元胞自动机系统。d是一个正整数,表示系统的维数;S是元胞的有限的离散的状态集合;N表示空间邻域内元胞的组合,包含各个不同元胞状态的空间矢量,记为:N=(S1,S2,S3,…,Sn),n 是邻域内元胞的个数;Si属于 Z(整数集合),i=(1,2,3,…,n);f是变化规则,Sn为将映射到S上的一个局部转换函数[1]。
1.2 模型建立
模型的建立需要考虑众多因素,如疏散路径的选择,疏散过程中人员行为的研究等。
1.2.1 建筑空间模型假设
将公共场所的布局设定在一个二维空间,按矩形方式对其进行均匀划分,每个网格为一个元胞,所有元胞共同构成元胞空间,每个元胞空间只能容纳一人。
元胞有三种状态(以二维数组B(i,j)表示):一被建筑或障碍物占据(以“2”表示),二被人员占据(以“1”表示),三为空(以“0”表示)。若元胞的烟雾达到一定浓度则会威胁人的生命。可以采用Von Neumann或Moore两种模型,如图 1 所示[2]。
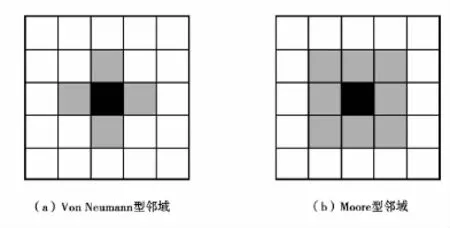
图1 元胞自动机邻居模型
以二维建筑平面左上角顶点为原点建立二维平面坐标系x-y,将网格在行列方向顺序排列,可确定任一元胞A(i,j)中心坐标(x,y)为:

1.2.2 人员模型假设
假定疏散人员具有相同的特征,在仿真开始同时井然有序地进行疏散,用元胞中心坐标来计算元胞至出口中心的距离。
1)初始位置:人员处于元胞自动机的某个单元格中,可以随机产生或预先设定。
2)移动方向:人员可以移动到周围4个或8个未被占据的元胞中。
3)冲突检测:当出现多个人员都选择同一个单元格时则需要进行冲突检测。在此引入个体竞争力W来解决冲突问题。

其中A表示疏散人员的个体特性,一般认为青壮年的A值高于老幼病残人员。D表示人员距该目标点的方向值,一般认为目标点处于人员的前后左右时其值小于处于4个对角线的方向距离值[3]。
1.2.3 人员疏散模型建立
1)人员疏散规则
首先,所有人员根据其所处网格的状态和邻域内网格的状态选择领域网格吸引力概率最大的一个网格;其次,在疏散时人员总是以寻找距离自己最近的出口为目标;最后综合网格位置吸引力概率及火灾场景排斥力概率得出人员下一步的目标网格[4]。图2为人员下一步可能的移动方向和概率。

图2 人员下一步可能的移动方向和概率
(a)网格位置吸引力概率

式中:d(i,j)—网格(i,j)到疏散出口的距离,maxd(i,j)—距离出口最大网格距离值,mind(i,j)—距离出口最小网格距离值。距离疏散出口越近,位置吸引力概率越大,反之越小。
(b)冲突避让规则
对于多个竞争力相同的人(状态值为“1”)同时竞争同一个空位网格(状态值为“0”)时,随机选取一个元胞进入该空位网格,其它元胞则退回原地,直到所有状态值为“1”的元胞都找到自己唯一的目标网格。
(c)火灾场景排斥力概率
将火源中心边缘网格分为五级(如图3所示),中心区域的一系列矩形区域为火源点,伤害力最大,边缘区伤害力较小,当距离达到一定程度后,火源对人员将无伤害。

式中:W2—火灾场景排斥力,xh—网格距离火源中心一系列矩形区域最外层的距离。

图3 火源排斥力范围
(d)综合影响力概率
对每个网格计算网格综合影响力概率:

式中:W1—网格位置吸引力概率,W2—火灾场景排斥力概率。为了保证出口对人员的综合影响力概率大于其周围的其他网格,故将火灾场景排斥力概率乘以系数0.5[5]。
2)人员行走算法
采取并行规则,即所有元胞的状态是同时发生变化的。每个元胞的下一个时间步的状态是由其邻域内所有元胞以及它自身当前状态决定,每个元胞每一时刻只能移动一步或者不动。采用元胞A(i,j)的 Moore型邻域,则元胞A(i,j)能以上、下、左、右邻域以及对角的四个领域或自身共九个邻域为下一时刻的目标网格。假设有两个出口,出口中心坐标为01(x1,y1),02(x2,y2)则可得 A(i,j)与距离其最近的出口0 距离:

3)边界与出口处的特殊处理
由于边界上的元胞不满足Moore型邻域的八个可能行走方向,特将初始二维矩阵的四周扩展一层并赋值为“2”即可满足邻域要求[6]。
2 仿真步骤和结果分析
2.1 人员疏散过程的仿真
2.1.1 人员疏散仿真流程
人员疏散仿真流程如图4所示。
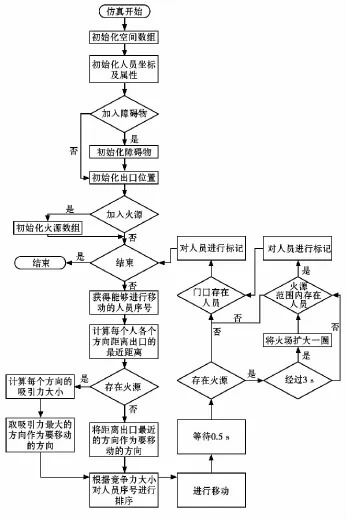
图4 人员疏散仿真流程
2.1.2 仿真模型的建立
本文对一个近似于一般超市,有两个出口,每个出口可同时出三个人,面积为30 m×30 m的虚拟场景下的人员疏散行为进行模拟,将空间划分为60×60的网格即共计3 600个网格,随机分布若干人。假设人员疏散时平均速度为1 m/s,则计算步长为:0.5 m/(1 m/s)=0.5 s。
2.2 仿真结果分析
2.2.1 建筑内结构不同情况下人员疏散过程的仿真
在出口位置固定的情况下考虑有无障碍物以及障碍物的摆放方式分别进行仿真模拟。图5为三种障碍物摆放方式示意图。


图5 三种障碍物摆放方式示意图
仿真人员疏散过程得:分别对三种障碍物摆放方式下人员疏散过程多次仿真结果显示,在每种障碍物摆放方式下全体人员疏散所用时间基本不变。比较三种障碍物摆放方式下全体人员疏散所用时间,三种障碍物摆放方式下全体人员疏散所用时间对照表如表1所示。
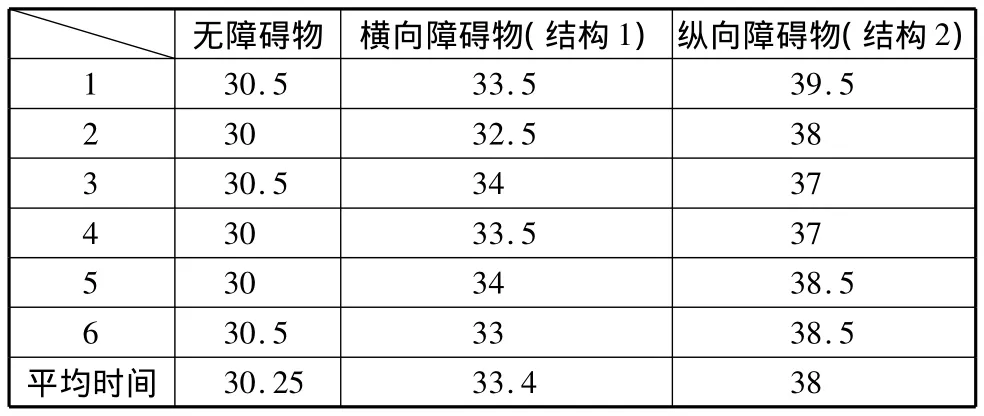
表1 三种障碍物摆放方式下全体人员疏散所用时间对照表
实验数据表明:建筑物内的结构特征对疏散效率有一定的影响作用,建议在大型建筑物内设置隔断或摆放大型物品货架时其位置最好与出口位置相对(与上述结构1类似),当火灾或紧急事件发生时人员能够快速对出口位置做出判断。
2.2.2 出口设在不同方位时人员疏散过程的仿真
仿真人员疏散过程得:分别对两种出口设置方式下有火灾发生时人员疏散过程进行仿真,多次仿真结果显示,在每种出口设置方式下每次全体人员疏散总时间相差不大。比较两种出口设置方式下有火灾发生时全体人员疏散过程所用时间,两种出口设置方式下有火灾发生时全体人员疏散过程所用时间对照表如表2所示。

表2 两种出口位置设置下全体人员疏散所用时间对照表
由于不同的出口设置可能会对人员疏散的过程有不同的影响,考虑了两种出口设置方式,一种为两个出口设置在对角线位置;另一种为出口设置在边界的同一侧。
在仿真结束生成的疏散人数与时间的关系图,表示出两种出口设置方式下有火源存在时的人员疏散时间的直观表示。如图6,7所示。

图6 出口设置为对角线情况下疏散人数与时间关系图

图7 出口设置为同一侧情况下疏散人数与时间关系图
表2以及图6,7的实验数据表明:建筑物出口位置的设置将会影响人员疏散过程,建议在大型建筑物内的出口尽量设置的过于分散,最后可以将出口设置在平面区域的对角线两头,当火灾或紧急事件发生时人员能够在最短的时间内疏散出去。
3 结束语
本文基于元胞自动机理论,建立了人员疏散过程的模型,运用JavaScript编写了仿真程序。利用程序进行了建筑结构不同即有无障碍物以及障碍物的摆放对疏散时间的影响及出口设在不同方位时人员的疏散过程两种情况的仿真,并对仿真结果作了分析,同时基于仿真结果给建筑物的出口及障碍物的摆放设计给出了合理建议。
[1]张培红,陈宝智.火灾时人员疏散行为规律[J].东北大学学报,2001,22(1):54 -56.
[2]Burstedde C,Klauck K,Schadschneider A,et al.Simulation of Pedestrian Dynamics Using a Two-dimensional Cellular Automaton[J].Physical,2001,295(3 - 4):507-525.
[3]孟俊仙,周淑秋,饶敏.基于元胞自动机的人员疏散仿真研究[J].计算机应用,2009,30(1):241-246.
[4]陶平,张小英,马恒亮.基于元胞自动机模型的人员疏散仿真研究[J].计算机仿真,2009(10):319-322.
[5]张培红,陈宝智,刘丽珍.大型公共建筑物火灾时人员疏散行为规律研究[J].中国安全科学学报,2001,11(2):22-26.
[6]陈全.人在火灾中的行为规律及计算机方针[D].沈阳:东北大学博士后研究工作报告,1997.

