一种高精度电压基准源设计方法

程 亮

(山西经济管理干部学院，山西太原030024)

在集成电路中，基准源包括基准电压源和基准电流源，其主要为电路提供稳定性较高的电压基准和电流基准。随着SoC技术的发展，基准源成为数模混合芯片的重要组成部分，基准源的优劣直接影响到整个系统的性能指标。

基准电压源通常给系统的其他模块提供高精度参考电压，广泛应用于数模转换器、模数转换器、线性稳压器和数模混合集成电路中。其目的是为电路系统建立一个与电源和工艺无关、具有确定温度特性的直流电压。

常规的带隙基准源温度系数一般都大于15 ppm/K，电源抑制比也不够理想，不能满足高性能系统的要求。本文采用高阶非线性和分段曲率两种温度补偿相结合的方法，获得了极低的温度系数。

1 电路原理

传统的一阶线性补偿采用VREF=VBE+VTlnn的方法，可以消除VBE的一阶线性项，而非线性部分则需要额外的电路来进行高阶项的抵消。具体设计电路如图1所示。其中，PNP管Q2的面积与Q1的面积比为N∶1。运算放大器的作用是使A、B两点电位近似相等，使得流过电阻R1的电流性质为正温度系数的电流。使电路中R2=R3，得到流过R2和R3的电流具有负温度系数，并且大小相等。通过正负温度系数电流叠加可知流过M1、M2、M3和Q3的电流与温度无关。进一步选取电阻R4=R5，使得流过R4、R5的电流与VT1n(T/T0)成正比。图1中基准电压通过计算，选择合适的R2、R1和N的数据，可以巧妙地消除VEB1的一次线性项;当R4=R2/(η－1)时，可以消除VEB1的高次项，从而实现基准电压温度特性的高阶补偿。

图1 高阶温度补偿电路

图2 分段曲率补偿电路

分段曲率补偿［1］的原理是当电路工作温度高于TH时，电路中增加高温补偿电流IH;当电路工作温度低于TL时，电路中增加低温补偿电流IL。

在图2中，当温度T＜TL时，M1、M2关断，M3、M4导通，产生低温补偿电流IL，此时IH=0。当温度T＞TH时，M3、M4关断，M1、M2导通，产生高温补偿电流 IH，此时 IL=0。当TL＜T ＜TH时，M1、M2 、M3、M4全部关断，IL=IH=0，曲率补偿电路失效。使用该方法可以大幅度减小温度系数。

2 电路设计

图3为本文设计的电路图，共由5部分组成，包括启动电路、正负温度系数电流电路、高阶补偿电路、分段曲率补偿电路和基准电压产生电路。

从图中观察可知，流过MP6和R1的电流为负温度系数电流，流过电阻R2的电流为正温度系数电流。此正负电流通过MP9和MP10进行镜像，两路镜像电流叠加后流过Q3，使得该电流与温度无关，再由R4和R3来完成高阶补偿。流过MP7和MP8的正温度系数电流就具有了高阶项，最终由MP11和MP12镜像两类电流来产生消除了线性项和高阶项的基准电压。

继续对基准进行分段补偿，得到最后的基准电压VREF=(IP+IN)(R5+R6)+(IL+IH)·R6可以通过改变MP20、MP19和MP15、MP16的宽长比来调节 IL和IH的大小，TH和TL这两个边界温度由MP18、MN8和MP14、MN6的宽长比来确定。

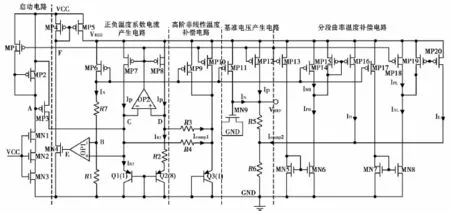
图3 温度补偿基准电压源电路

3 结论

本设计基于0.35 μm标准CMOS工艺模型，使用HSPICE仿真器对电路进行仿真模拟。在VCC=3 V，T=25℃的典型条件下，得到基准瞬态值为505.87 mV。如未特别说明，仿真在TT工艺角条件下完成。

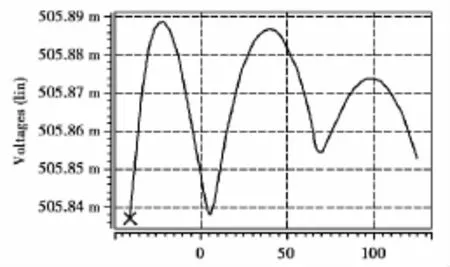
图4 温度特性仿真波形(505 mV)

在－40℃ ～125℃温度范围内对电路进行仿真，只进行一阶线性补偿时，温度系数达到了19.2 ppm/℃，当采用高阶非线性温度补偿后和分段曲率温度补偿后，温度系数减小到0.62 ppm/℃。最终的仿真波形如图4所示。基准在全温度范围内变化约50 μV，能够满足高精度电路系统对温漂的要求。

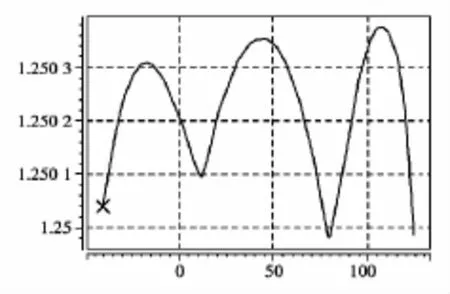
图5 温度特性仿真波形(1.25 V)

根据上述公式计算，更改R5、R6的阻值，把基准电压在25℃下瞬时输出值调节到1.25 V。基准电压在165℃的全温度范围内仅仅变化了0.4 mV，计算得出温度系数为1.93 ppm/℃，仿真结果如图5所示。

图6 温度特性仿真波形

图6中的仿真结果是在不同的工艺角下面得出的。最大的温度系数出现在FF工艺下，经计算温度系数为2.93 ppm/℃。

本文采用高阶温度补偿和分段曲率补偿相融合的思路设计的高精度基准电压源，在最极端工艺条件下，在165℃的全温度范围内，输出的基准电压变化小于0.3 mV，温度系数小于3 ppm/℃。能够很好地满足亚微米条件下ADC或DAC系统芯片对基准电压的性能要求。

［1］Ming－Dou Ker，Jung－Sheng Chen，Ching－Yun Chu.New Curvature－Compensation Technique for CMOS Band gap Reference with Sub－1－V Operation［J］.IEEE Journal of Solid State Circuits，2005.