移动单站测向数据量对定位精度的影响

徐铂韬

（中国电子科技集团公司第五十四研究所，河北石家庄050081）

0 引言

机载移动测向站以其机动性和灵活性强等特点，越来越广泛的应用于军事和民用领域。在与用户的长期接触和交流中，发现使用者经常会提出这样的问题:如何才能准确定位。得到的答案往往只是:尽量多的获取测向数据有助于提高定位精度。但是，获取更多的测向数据意味着消耗更多的工作时间，并且定位精度不可能随着测向数据量增加而无限提高。那么，获取什么样的测向数据对提高定位精度最有效？获取多少测向数据为佳？根据这些移动单站实际使用过程中的问题，首先以非线性最小二乘估计下的移动单站多次测向数据交会定位为例给出定位误差模型，然后分析了测向数据量和数据有效性对定位精度的影响，并进行了仿真[1－5]。

1 交汇定位误差模型

移动测向站交汇定位[6，7]是利用不断变换测向站所在的位置，对同一固定辐射源目标进行多次多点的测向，然后通过几何交会的方法确定辐射源的位置，如图1所示。

图1 交汇定位

图1中，假设移动单站在移动线路上的位置点Ai（xi，yi）对目标E（x，y）进行了i次测向（i=1，2，…，n，以下同），方差为σxi、σyi的正态随机变量。测向角θi的测量噪声是零均值的高斯白噪声υi，其方差为σθi，交会定位误差如图2所示。

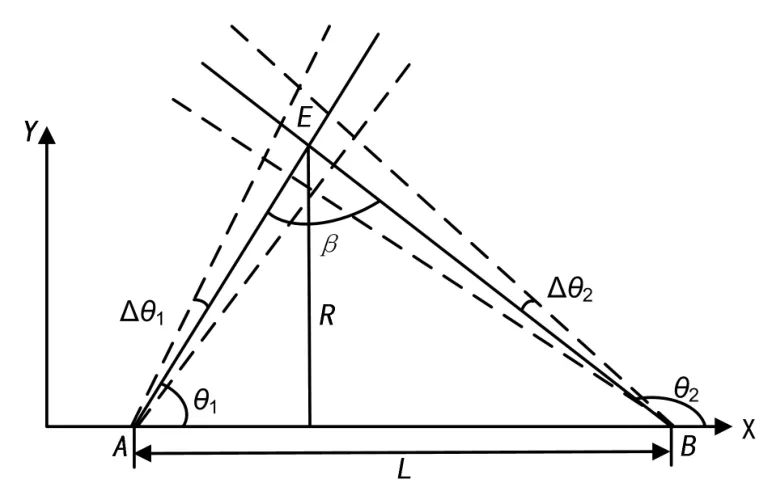
图2 测向误差与交汇定位误差

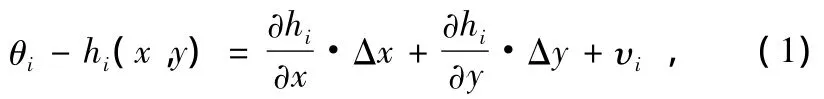
那么式（1）可简化为:

Z=H·W+V，

其中:

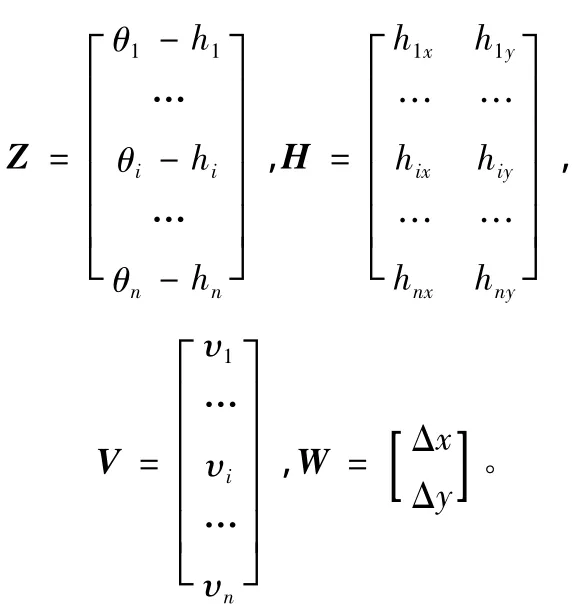
此时W的最小二乘估计为那么其协方差矩阵为:

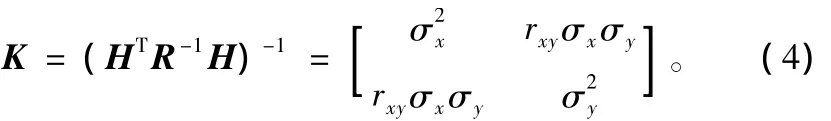
由于移动测向站交会定位的误差区域并不固定，但由于测向数据的误差相对较小，当移动测向与目标之间的距离相对较小时，可将目标误差范围近似为圆形或椭圆形区域。那么通过圆概率误差分析可知:当两次测向观测点到目标E（x，y）的距离相同，并且两次观测点之间的距离为到任一观测点到目标距离的1.414倍时，其目标定位圆概率误差最小。也就是说，能够令目标定位圆概率误差最小的两次测向数据对提高目标定位精度贡献最大。但是，在实际过程中，并不能保证能够获得这样的测向数据，在一般情况下，除了合理的规划移动测向站工作路线外，还需要一定的有效测向数据量，接下来将分析测向数据量对定位精度的影响。

2 测向数据量对定位精度的影响分析

一般来说，某个测向系统在短时间内其测向精度[8－11]性能不会产生很大变化，那么可以认为该移动测向站在工作时每次测向的误差不变，即有

考虑到在实际工作中，移动测向站在相对较短的时间内移动的距离相比其到目标的距离往往要小得多，那么可以令r1=r2=…=rn=r。又令交会角βij=θj－θi，简化式（5）可得:

从以上分析可知，要提高目标定位精度[12－15]，也就是要获取最小σ2时的交会角βij的大小和数量，也就是令的最大值。交会角βij与F的关系如图3所示。

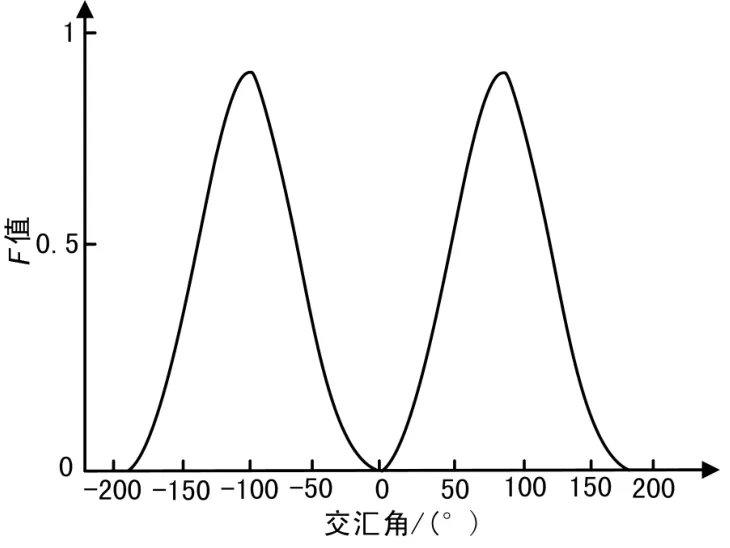
图3 交会角与F的关系

由对模型的分析和仿真结果可知:

通过以上分析可知，当利用2条交会角成90°的测向数据进行定位计算时，可获得相对较高精度的定位结果。但是在实际使用过程中，由于工作区域和路线的限制，有可能无法获取交会角达到90°的测向数据，那么应该合理规划移动测向站的工作路线，使其获取的测向数据中的交会角尽量接近90°。另外，上面在做目标误差分析时，将目标误差范围近似为圆形或椭圆形区域，但实际误差区域应为四边菱形区域，因此当在交会角最接近90°的2条测向数据之外的其他测向数据对缩小菱形误差范围有一定的贡献。但是由于是这种贡献相对较小，并且实际情况较为复杂，不做过多的分析。

由实际工作经验可知，在交会角最接近90°的2条测向数据之外，再选取使该交会角均分的一到2个测向数据最佳。例如:在获取的测向数据中，交会角最接近90°的2条测向数据的交会角为66°，那么再选取与该测向线交会角接近33°一条测向数据，或交会角接近22°和44°的2条测向数据即可，再增加其他的测向数据对提高定位精度的作用相对来说就很小了。由此可见，在实际的测向定位工作中不能一味的追求获取大量的测向数据，获取过多的测向数据意味着增加系统的工作时间和处理数据量，因此应该综合考虑测向定位系统的工作能力和目标区域范围，合理规划工作路线，在此基础上尽可能多的收集对提高定位精度贡献大的测向数据。

3 结束语

研究了移动测向站交会定位模型，推导出影响定位精度的关键因素和测向数据量与定位精度之间的关系，说明了并非测向数据量越大定位精度越高，关键在于交会角是否能达到最佳角度。根据这一结论，提高目标定位精度应该依此为原则规划和修正移动测向站的工作路线，解决了移动测向站在实际使用过程中如何制定工作计划的问题。该问题的研究，使移动测向定位系统在制定工作计划方面有了指导性原则，对于实现移动测向站快速、有效和高精度的确定辐射源目标位置有着重要的理论意义和实际使用价值，并可推广到相关项目中。

[1]翟庆伟.机载单站无源定位技术研究[J].无线电工程，2007，37（3）:50－52.

[2]邱丙益，盛莹，刘春茂.基于TDOA的短基线测向精度分析与仿真[J].无线电通信技术，2013，39（1）:67－69.

[3]崔弘珂，王玉林.三机时差频差联合定位精度分析[J].无线电工程，2011，4（7）:21－23.

[4]刑翠柳，陈建民.多站无源时差定位精度分析[J].无线电工程，2012，42（2）:32－34，48.

[5]赵琨，何青益.基于GDOP的三站时差定位精度分析[J].无线电工程，2012，42（5）:15－17，33.

[6]修建娟，何友，王国宏，等.测向交叉定位系统中的交会角研究[J].宇航学报，2005，26（3）:282－283.

[7]孙彪.基于单目视觉的运动目标跟踪定位[J].四川兵工学报，2010，31（4）:85－86.

[8]刘俸才，谢明红，颜国霖.双目立体视觉系统的精度分析[J].计算机工程，2011，37（19）:280－282.

[9]袁铭，苏显渝，刘晓青.影响摄像机标定精度的因素分析[J].光学与光电技术，2010，8（4）:18－21.

[10]卢发兴，高波，邢昌风，等.测量站数量对多站测向交叉定位精度的影响[J].火力与指挥控制，2011，36（2）:50－52.

[11]汪珺.测向交叉定位技术[J].电子科技，2011，24（7）:129－131.

[12]王志刚，芮国胜，张磊.基于Bootstrap滤波的单站无源定位算法[J].海军航空工程学院学报，2005，20（2）:319－321，328.

[13]廖平，付忠，刘刚.采样率波算法在单站无源定位中的应用[J].电讯技术，2006（4）:28－31.

[14]邓新蒲.运动单观测器无源定位与跟踪方法研究[D].长沙:国防科学技术大学，2000:31－32.

[15]单月晖.空中观测平台对海面慢速运动目标单站无源定位跟踪及其关键技术研究[D].长沙:国防科学技术大学，2002:1－16.