基于随机-模糊耦合的污染场地健康风险评价及案例
徐 亚,朱雪梅,刘玉强,能昌信,董 路
(中国环境科学研究院固体废物污染控制技术研究所,北京 100012)
基于随机-模糊耦合的污染场地健康风险评价及案例
徐 亚,朱雪梅*,刘玉强,能昌信,董 路
(中国环境科学研究院固体废物污染控制技术研究所,北京 100012)
采用模糊理论描述风险评价过程的模糊不确定性,采用概率理论描述随机不确定性,同时为解决模糊数计算过程复杂的问题,将模糊变量表示成均匀随机变量的函数,用 Monte Carlo算法模拟模糊变量之间的函数运算,从而实现模糊-随机方法的耦合.为验证该模糊-随机耦合模型的有用性,选取青海某汞化工污染场地进行案例研究,通过与 RBCA模型比较,验证了该模型的基本精度,且能较好地表征场地参数的不确定性对风险评价结果的影响.案例分析的结果表明:人群主要暴露途径为经口摄入,贡献率为 80%左右;正常暴露情形下,该场地的健康风险水平为0.28,风险水平可以接受,最不利情况下的健康风险风险水平为1.28,最不利情况出现的概率小于等于1%;该场地对人群的健康风险随着时间减小,在第6年左右其风险减小至可接受水平,建议无需对场地开展污染治理,只需在污染物高峰段(第1~6年或第6~8年)为居民提供替代水源以截断暴露途径,待场地污染水平自然衰减.
模糊-随机;暴露评价;不确定性;风险评价
污染场地的健康风险评价指针对某一污染场地进行研究以评价其对人体健康造成危害的可能性,进而为场地后续的治理和使用提供决策支持.显然风险评价结果越明确(不确定性越小),越便于决策者进行管理和决策;风险评价结果越模糊,决策者越难以抉择[1-3].因此,在评价过程中,评价者应该尽量减小评价结果的不确定性.而对于难以减小的不确定性因素,则应在风险评价的最后阶段予以定性乃至定量的描述[4].
国内外许多学者在这方面开展了有益的探索,如 Lee等[5]基于模糊集方法评价了地下水中污染物的人体健康风险;Kumar等[6]应用网络分析法(ANP)处理了风险评价过程的模糊变量; Goodrich等[7]运用Monte Carlo方法定量描述了水文地质和地球化学参数对地下水水流和溶质运移模型的影响,并将模型结果用于暴露评估; Hamed等[8]基于一阶和二阶可靠性方法考虑了参数不确定性对风险评估结果的影响; Batchelor等[9]将一些场地参数用概率分布函数表示,并在此基础上建立了随机风险评价模型.
上述模型对不确定性的研究多基于单一的随机模型(概率模型)或模糊集模型,近年来基于随机-模糊结合的模型得到大量应用,如Guyonnet等[10]在进行健康风险评价时分别采用概率分布函数和隶属度函数表征不同类型的不确定性;Li等[11-12]构建了模糊-随机耦合的地下水污染风险评价,用概率分布表征参数的不确定性用隶属度函数表征风险结果的不确定性,并将之应用于加拿大西部一个石油烃污染场地的地下水污染风险评价;金菊良等[12]则用随机模拟方法模拟三角模糊数,建立了水环境风险评价的随机模拟与三角模糊数耦合模型.
1 随机-模糊耦合模型
广义的不确定性包括模糊不确定性和概率不确定性[13-14].参数的概率不确定性通常用概率分布函数来描述,并基于Monte Carlo算法通过确定性模型生成输出值的概率分布.而参数的模糊不确定性则用隶属度函数来表征.当样本数据比较丰富时,采用概率不确定性来描述参数的不确定性可以取得较好的结果;而模糊不确定性适用于较少或不精确的数据资料的处理和随机信息的表征,同时在处理和表达模糊信息时也有一定优势[15-16].然而模糊数在实际应用过程存在一定局限性,主要问题是目前对于模糊数的乘法、除法和函数运算尚不够严谨、操作过程比较复杂,而若采用模糊数的截集技术进行计算,实现过程又过于复杂,同时难以适用于模糊数的函数运算[10].
1.1 模糊变量和随机变量的耦合方法
假定Y为模糊变量,y为模糊变量Y在论域U中的可能值变量,χ为随机变量X在样本空间内的可能取值.若y与χ存在函数关系y=f(χ),则可将模糊参数的模糊不确定性用概率分布表示,从而实现模糊性-随机性的耦合,进而利用 Monte Carlo方法解析输入参数不确定性(包括模糊不确定性和概率不确定性)对风险后果的影响.
那么问题的关键是找到模糊变量值 y与随机变量值 χ的函数关系.以常见的三角模糊数为例进行说明,其基本原理如下:
假定模糊变量Y的上限值和下限值分别为a和 c,b为最可能值,那么模糊效用(a、b、c)表示.其隶属度函数为:
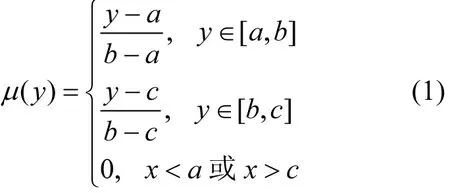
式中:y为模糊变量Y在论域U中的可能值变量.
模糊变量Y的隶属度函数如图1所示,将μ(y)除以μ(y)的曲线与y轴围成的面积0.5(c-a),得到的值可作为三角模糊数A的可能性概率密度函数.

采用逆变换法[17]将上式变换,得到模糊变量Y的可能值y的随机模拟公式:
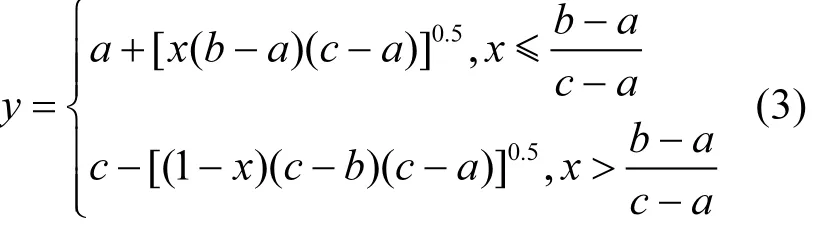
式中:X是参数为(0,1)均匀随机变量;χ是X的可能值.
类似的,其他类型的隶属度函数,如梯形、正态型和Sigmiod型分布,都可按照上述方法处理.如此,就可将模糊不确定性参数用概率分布函数表示,从而将模糊不确定性参数和概率不确定性参数耦合起来(图1),并基于Monte Carlo方法计算并解析输入参数不确定性对风险结果的影响.
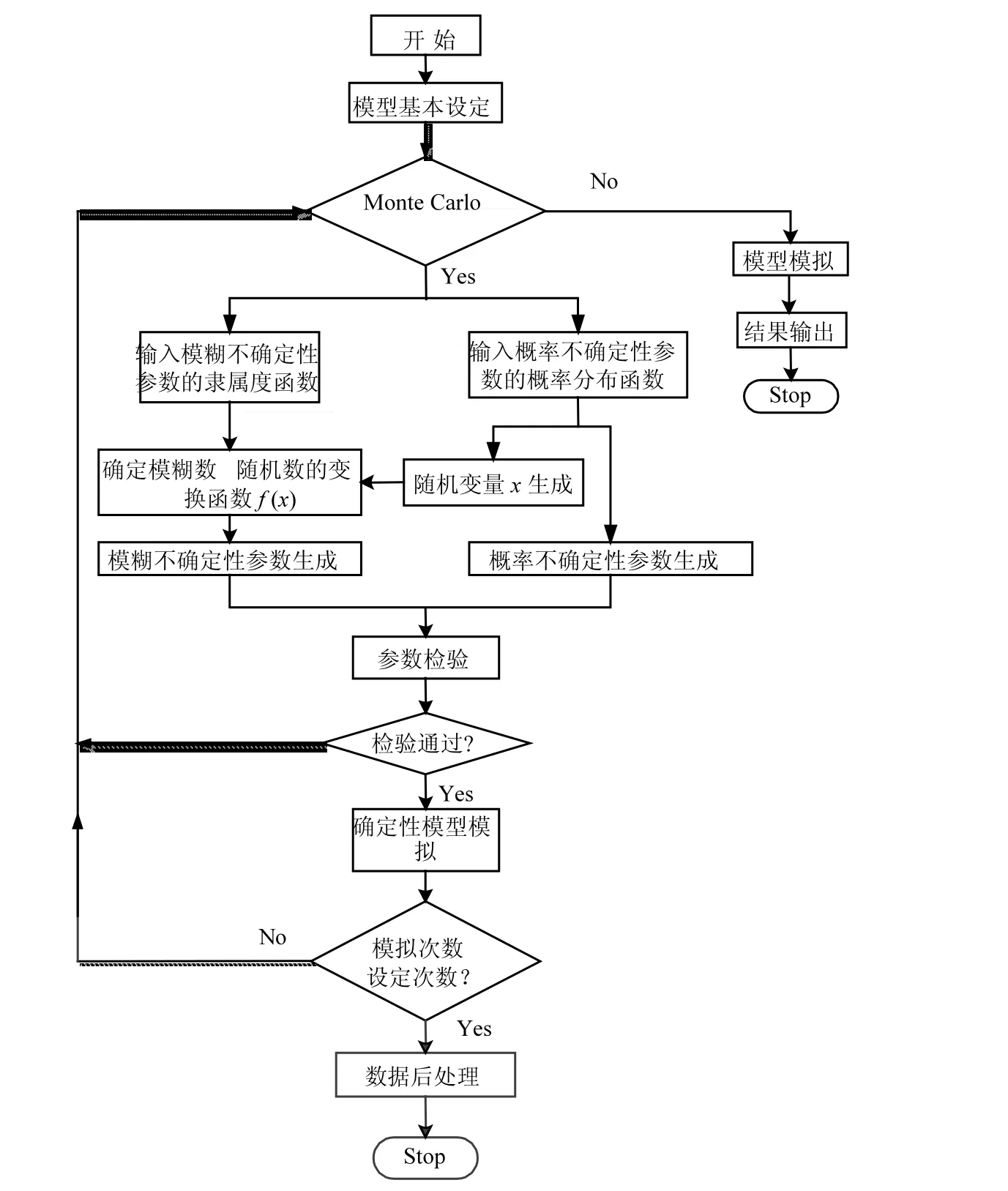
图1 基于模糊-随机耦合的暴露过程评价过程Fig.1 The coupled fuzzy-stochastic model of exposure assessment
1.2 隶属度函数和概率分布函数及相关统计参数的确定
1.2.1 隶属度函数 参数的模糊不确定性用隶属度函数表示,隶属度函数的特征参数为 a(可能最小值),b(最可能值)和 c(可能最大值),通常用变量X的样本均值来表征最可能值.最小值和最大值通过下式计算:
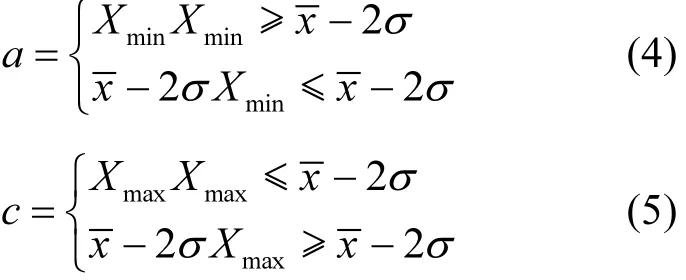
式中:Xmin和Xmax分别为变量X的最小实测值和最大实测值;为样本均值;σ为样本标准差.
1.2.2 概率分布函数 参数的概率不确定性用概率密度函数(PDF)来描述.污染场地风险评价中常用的概率分布函数包括 Normal分布、Uniform分布、Log-normal分布、Beta分布和Poison分布等.一般气象学参数如降雨量、蒸发量服从 Normal分布[18];水文地质参数中渗透系数和弥散度分布服从对数正态分布[19];孔隙度和延迟因子服从正态分布[20].
若已知参数的概率分布类型,可直接根据相关公式求得其方差、均值等特征参数;若参数概率类型未知,则需要先对其分布类型进行先验判断,假定其分布类型后,通过假设检验法确定其是否属于该假定分布.
2 案例研究
受场地中污染物浓度、场地水文地质条件、自然气象条件不确定性等诸多不确定性的影响,敏感人群的暴露浓度存在着明显的不确定性,最终的健康风险也存在着极大的不确定性.本文以青海某汞污染场地为例,应用上述随机-模糊耦合模型刻画污染场地及暴露过程参数的不确定性对最终风险的影响.
2.1 研究区概况
研究对象为青海省某汞化工企业搬迁后的遗留场地,主要产品为聚氯乙烯和烧碱,主要生产工艺为汞法烧碱和电石法PVC.历史上,该厂产生的大量汞废渣被就地堆放在厂区及周边地区,对周边土壤及地下水质量及人体健康构成严重危害.2011年根据国家环保要求和淘汰落后产能的产业政策,该公司宣布停产后拆除所有设施并完成废渣堆的处理工作,然而汞废渣长期堆放过程中形成的污染土壤仍对周边居民健康形成严重威胁.图2为研究区概况.
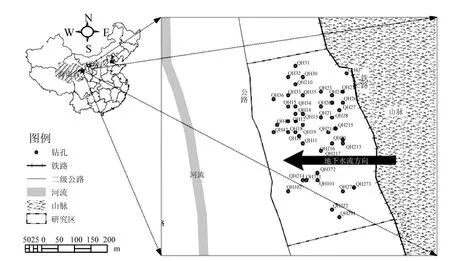
图2 研究区概况Fig.2 Overview of study area
2.2 危害识别
场地污染调查采用分区域网格化动态布点方法,逐步细化确定铬污染程度和范围,最终完成47个点位采样,获得1269个土壤样品.土壤样品用王水水浴消解(GBT22105.1-2008)[21],消解液用 AFS-3000型原子荧光光度计分析测定总汞含量.除汞外的其他重金属测定用ICP-MS进行.分析结果显示大部分样品土壤中总汞浓度在30~68.7mg/kg,最高达142mg/kg,其他重金属未发现超标现象. 根据《污染场地风险评估技术导则》(报批稿),污染场地土壤风险评价中汞的启动值分别为 5mg/kg(住宅用地)和 49mg/kg(工业和其他用途),因此判断该场地进行再次利用时需要进行风险评估,主要污染物为Hg.
为污染区域的Hg浓度,采用Walsh's Test分析法识别并去除了样品数据中的浓度异常偏大值,用经验最小值代替了未检出值,利用假设检验法对Hg浓度数据的3种假设分布形态(正态分布、对数正态分布和Gamma分布)进行了拟合优度检验,结果表明污染场地的 Hg浓度数据服从参数为(60,10)的正态分布.
2.3 暴露评估
2.3.1 暴露途径分析 人体暴露途径一般包括:饮用水、动植物和土壤的摄入;大气的挥发物和颗粒吸入;土壤、地表水和地下水的皮肤接触.本案例中地表已做硬化处理,同时 Hg的存在形态主要以不挥发性形态存在,因此不存在大气挥发物和颗粒吸入以及土壤摄入;研究区为商业用地也不存在动植物摄入和地下水皮肤接触. 因此其主要暴露途径为饮用水的摄入和地表水的皮肤接触,暴露过程如下:地下径流从东部山区往西流动,流经厂区的污染土后,污染土中的可溶性Hg在吸附解析作用下溶出并随地下水迁移,最后排泄至研究区西部的河流中,人群通过在河中游泳和饮用河水发生暴露.河流东岸处的地下水浓度可视为人体的暴露浓度.
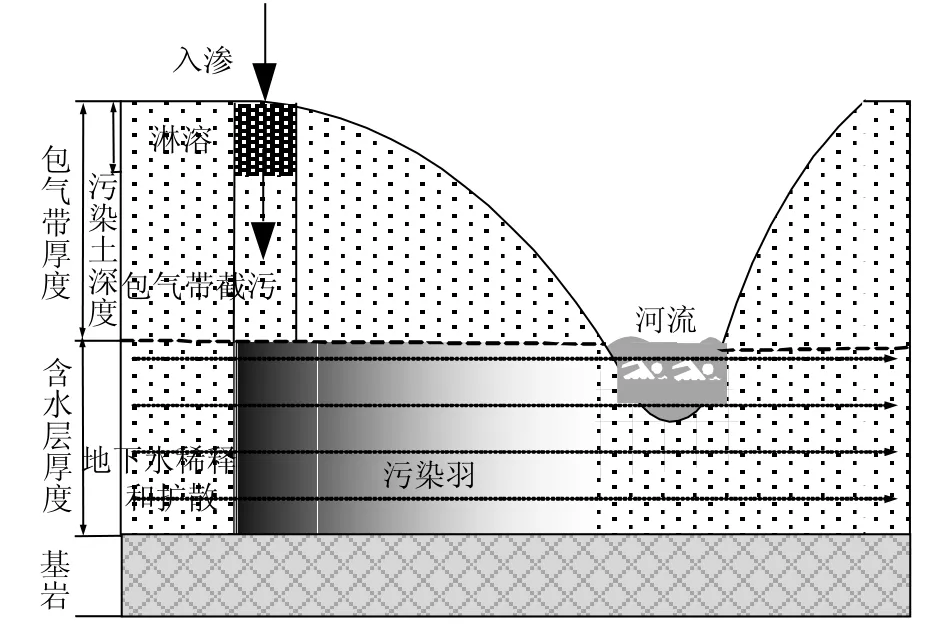
图3 暴露过程概化Fig.3 Conception model of exposure process
2.3.2 暴露点浓度 计算 Hg从污染土壤中迁移至暴露点需要经历两个过程(见图3),首先是土壤中污染物在地表入渗作用下的垂向迁移,在到达地下水面后在地下水水力梯度作用下从东向西运动进入河流中.假设污染物在包气带中的垂向迁移和在地下水中的水平运动分别服从一维瞬态方程和平面二维瞬态方程,考虑污染物的一阶降解和一阶反应,可以分别得到污染物浓度在土壤和含水层中分布为:

式中:Ci和Cwi分别为Hg在包气带和含水层中的浓度;t为时间;Z为包气带模型的深度坐标,向下为正;χ和y为饱和带模型中的χ和y坐标;v为补给强度,等于降雨入渗强度 I;R为滞后因子,等于1+(ρ/n1)Kd;D为动力弥散系数;Ki为污染组分i的一阶降解系数;Dχ和Dy分别为χ、y方向上的弥散系数;uχ为地下水流速;λ为一级反应常数;n1为包气带的孔隙度.
初始条件:浓度初值即为包气带和含水层中,各污染组分的背景值,因此初始条件可设为:

式中:Cb2和Cwb,分别为包气带和含水层中Hg的背景值;Cb2,污染土壤中 Hg的浓度值;Dc为污染土深度;D为包气带厚度.
边界条件:对于包气带,其上边界为零浓度边界,下边界为零浓度梯度边界:
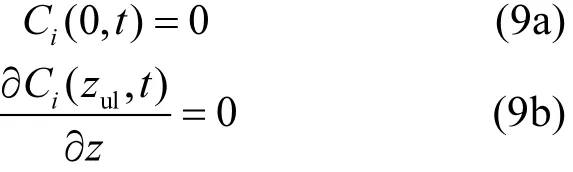
式中:zul为包气带底部的深度.
对于含水层模型,其边界条件为:
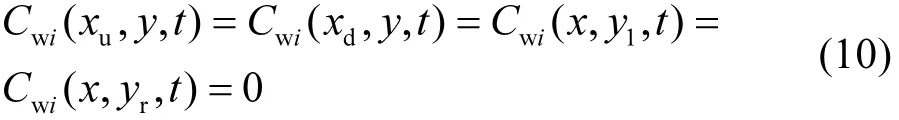
式中:χu、χd、yl和yr分别表示含水层模型上、下游边界和左右边界.
控制式(6)和式(7),结合其约束条件(8)~(10),可以用有限差分或者有限元法求解得到给定参数条件下暴露点的浓度.结合模糊-随机耦合模型就可以得到参数不确定条件下暴露点浓度的概率分布,暴露评价过程涉及的主要参数及其分布类型如表1所示.
2.3.3 人体摄入量计算 如 2.3.1所述,场区居民可能通过两种途径摄入 Hg:通过饮用河水和在河中游泳.
通过饮用途径的摄入量可根据下式计算:
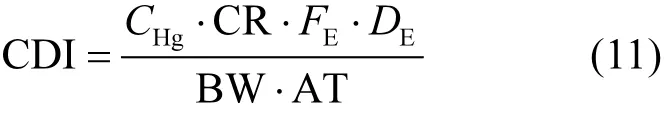
式中:CHg为暴露浓度,mg/L;CR为饮用水摄入速率,成人取2L/d(US EPA推荐数据);FE为暴露频率,d/a;DE为持续暴露时间,a;BW 为体重,取60kg;AT为平均时间(对致癌物质取人类平均寿命70a共有的天数[22];对非致癌物质取DE和 FE的乘积,即将危害平均到整个暴露作用期),d.
通过游泳时皮肤接触的摄入量根据下式计算:
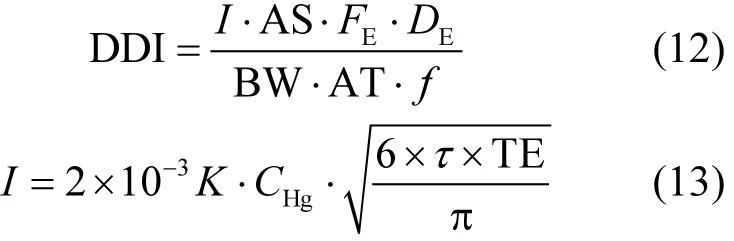
式中:AS为人体表面积,cm2,取 16600;FE为暴露频率,次/年,取105;f为肠道吸附比率,取1;I为每次游泳时皮肤对污染物的吸附量,mg/(cm2·次);K为皮肤吸附参数,cm/h,取 0.001;τ为延滞时间,h,取1h;TE为游泳时间,h,取0.4h.
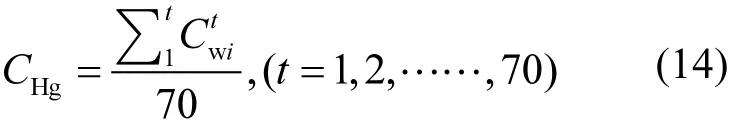
2.4 毒性评估和风险表征
汞为非致癌化学物质,因此本研究考虑其非致癌效应,其经口摄入和皮肤接触参考剂量 RfD分别为3.00×10-4和2.10×10-5mg/(kg⋅d)[23].
人群通过饮用水而产生的非致癌风险为:

人群通过游泳接触含Hg河水的非致癌风险为:

其中:RfDo和 RfDd分别为经口摄入和皮肤接触参考剂量.
通过不同暴露途径产生的综合风险为:

3 结果与讨论
3.1 暴露点浓度
由暴露评估模型可以计算得到暴露点处任意时间浓度的累计概率分布,选取浓度累计概率分布的1%,5%,10%,50%,90%,95%和99%分位值表征最乐观,较乐观、乐观、正常、不利、较不利和最不利条件下的暴露点浓度,绘制其历时曲线(图4).从图中可知暴露点浓度随着时间逐渐增加,在第7年达到最大值,随后逐渐减小,至25a左右衰减为零.

图4 暴露点Hg浓度的历时曲线Fig.4 Duration curve of Hg concentration in exposure point
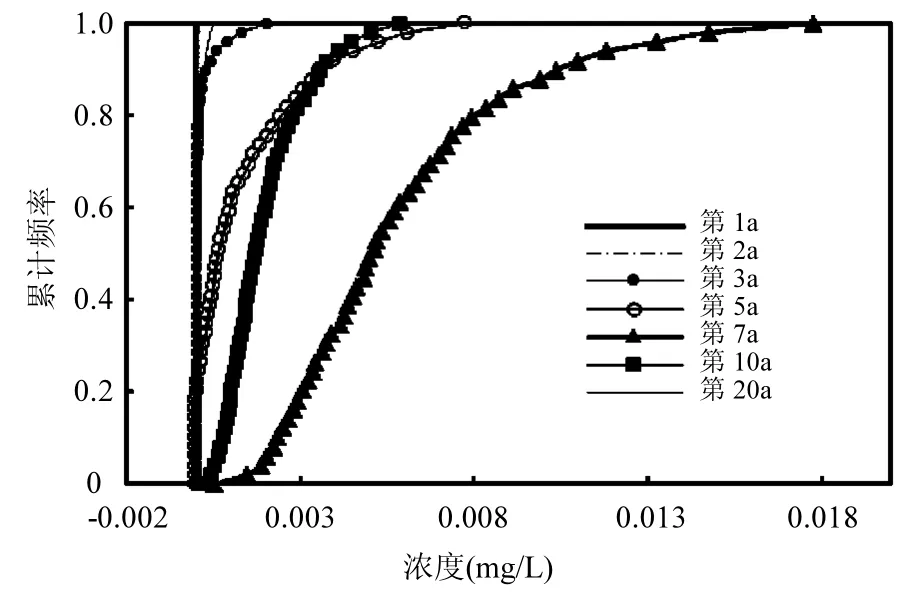
图5 暴露点Hg浓度的累计概率分布Fig.5 Cumulative frequency distribution of Hg concentration in exposure point in different year
同时由于暴露过程参数不确定性的影响,暴露点浓度也存在较大的不确定性.以第7a为例,最不利情况下(降雨量大,包气带厚度小,源强浓度大等)其暴露点浓度高达 0.023mg/L;最乐观情况下(降雨量小,包气带厚度大,源强浓度小等)其暴露浓度低至0.001mg/L;而正常情况下的暴露浓度则为 0.005mg/L.若以式(18)定量计算暴露过程的不确定性,则本案例情形下的不确定性高达5.
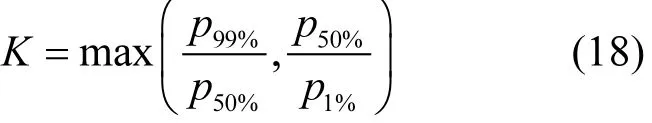
不同年份暴露点浓度的累计频率分布如图5所示.从图中可知,在不同年份暴露点浓度的不确定性不同,第7a不确定性最高,第10a次之,随后为第5a、第3a、第20a、第40a、第70a和第2a,第1a的不确定性最小.
3.2 风险评价结果
根据式(11)~(17),结合暴露点的浓度值(图4),计算得到该污染场地通过饮用途径和游泳途径暴露的非致癌风险值,结果见表2.
同时为验证本模型风险评价结果的基本精度,将本模型模拟结果(最不利条件)与RBCA模型结果比较(取相同参数,不确定性参数取最不利值),结果见图7.RBCA模型是由美国 GSI公司根据美国试验与材料学会(ASTM)“基于风险的矫正行动”(RBCA)标准开发,该模型除可以实现污染场地的风险分析外,还可用来制定基于风险的土壤筛选值和修复目标值,在美国各州、欧洲一些国家和我国台湾地区都得到了广泛应用.

表2 不同暴露情境下风险评价结果Table 2 Model result under different exposure scenarios
根据图7:RBCA模型计算的经口、经皮肤的非致癌风险以及综合风险值分别为 1.17、0.24和 1.41,与本模型比较,相对误差分别为 9.4%、9.1%和 9.2%.这说明本模型的基本精度合理,可用于污染场地的风险评价研究.比较不同暴露情景下(最乐观,较乐观、乐观、正常、不利、较不利和最不利条件下)的非致癌风险值,最不利条件下的综合风险值为 1.28,最乐观条件下的综合风险值为 0.07,相差 18倍,说明本场地条件下的风险评价结果具有较大的不确定性.不确定性的主要来源是场地暴露过程参数的不确定性,包括降雨量的随机性、污染物空间分布的不均匀性、水文地质参数的时空变异性等.若考虑最不利暴露条件下的健康风险,则其风险大于1,不可接受,但该不利暴露条件出现的概率很小(小于等于1%).
3.3 风险管理
根据表2,本案例中经口摄入Hg的非致癌风险为 1.06,经游泳过程皮肤接触含 Hg河水导致的非致癌风险为 0.22,故经口摄入 Hg为主要的暴露途径,可以考虑为居民提供替代饮用水源以降低其健康风险.
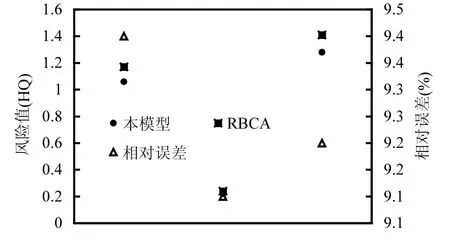
图6 RBCA模型结果的比较Fig.6 Results of comparison between this coupled model and RBCA model
假设居民从第 i年开始连续暴露(暴露时间仍取我国居民平均寿命 70a),根据式(18)计算得到从不同年份开始暴露的暴露浓度,并将暴露浓度代人式(11)~(13)计算得到从不同年份开始暴露的居民的人体健康风险值(图 7).从图 7可知,在持续暴露的时间一定(70a)的条件下,开始暴露的时间越早,健康风险越大. 在第 1年开始暴露的居民,其人体健康风险最大(综合风险值 1.28,经口暴露风险值1.06).在第3.7年开始暴露的居民,其经口暴露的非致癌风险值已降低到可接受水平(HQ=1);在第5.6年开始暴露的居民,其综合风险值也降低到到可接受水平.
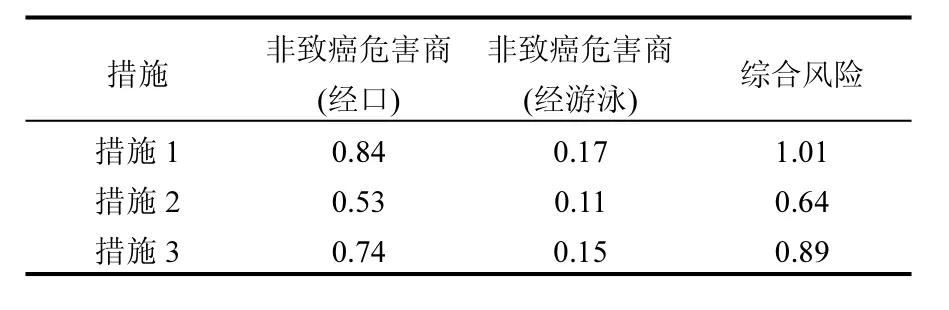
表3 不同风险应对措施下的人体健康风险Table 3 Risk result under different risk management measurements
同时根据图4所示,暴露点的浓度在第7a达到最大,其次为第6a和第8a,因此分别考虑3种措施下的人体健康风险:在第7a为该区域居民临时提供其他生活水源;在第6~8a为该区域居民提供其他生活水源,以避免在污染物浓度高峰时的暴露;以及措在第1~6a为该区域居民提供其他生活水源. 同样根据式(11)~(13)和式(18)计算人体健康风险值(表3),在采取措施1的情况下,经口暴露的人体健康风险值降至 0.84,小于可接受风险水平,但综合风险值为1.01,略高于可接受风险水平;而由于污染场地渗滤液污染地下水造成的人体健康风险也可降低到可接受水平;采取措施 2和措施3条件下,经口暴露非致癌风险和综合风险值均降至可接受水平. 因此建议无需对该场地进行修复处理,只需在第1~6a或6~8a,为居民提供替代生活水源,短暂截断暴露途径.
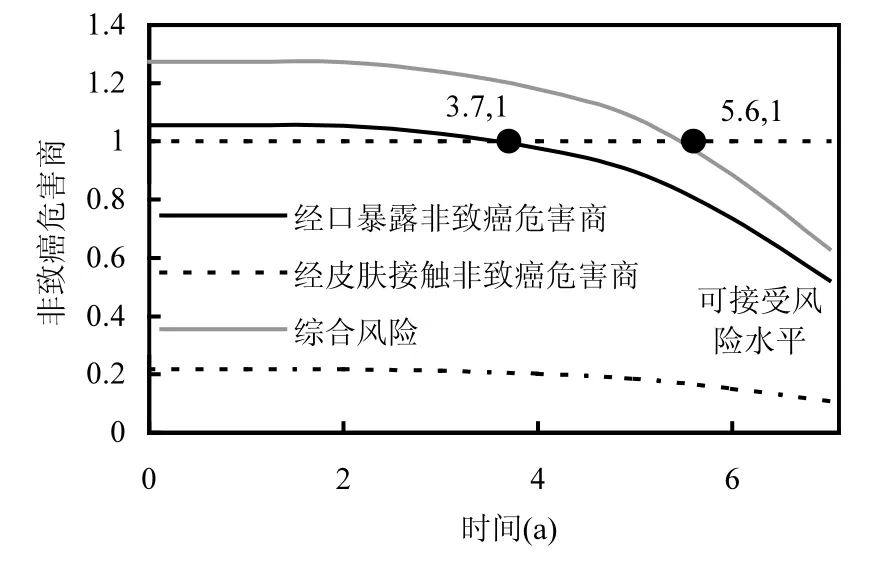
图7 风险值随时间变化曲线(最不利暴露情景)Fig.7 Duration curve of HQ under the most unfavorable condition
4 结论
4.1 应用逆变换法将污染场地风险评价中的模糊不确定性用随机方法表达,从而建立了污染场地暴露评价的模糊-随机耦合模型,应用该模型评估了青海某重金属污染场地的环境风险,结果表明模糊-随机耦合模型的模拟结果与RBCA模拟模拟结果的相差不超过10%,结果基本准确.
4.2 本案例中,经口摄入是构成人体健康风险的主要暴露途径,对整体风险的贡献约为 83%左右;受场地暴露过程参数不确定性影响,风险评价结果存在较大不确定性(不确定性系数等于5),正常情况下,该污染场地对人体的综合风险为0.28,可以接受;在最不利条件下,综合风险为 1.28,不可接受.最不利条件出现的概率小于等于1%.
4.3 由于包气带的降解和含水层的自然稀释作用,暴露点浓度会随着时间逐渐衰减,其风险水平也逐渐降低.因此可以考虑在污染物高峰段(第1~6a或第6~8a)为居民提供替代水源以截断暴露途径,待场地污染水平自然衰减,无需进行场地修复处理.
[1] Roland W S. Decision making under uncertainty in case of soil remediation [J]. Journal of Environmental Management, 2006, 80(2):132–147.
[2] Michael J C, James T P. Identifying and reducing uncertainty in decision making, decision making in natural resource management: a structured, adaptive approach [R]. John Wiley and Sons, Ltd, 2013:192-231.
[3] 刘年磊,蒋洪强,吴文俊.基于不确定性的水资源优化配置模型及其实证研究 [J]. 中国环境科学, 2014,34(6):1607-1613.
[4] Jianbing L, Gordon H, Huang B, et al. An integrated fuzzystochastic modeling approach for risk assessment ofgroundwater contamination [J]. Journal of Environmental Management, 2007, 82:173–188.
[5] Lee Y W, Dahab M F, Borgardi I. Fuzzy decision making inground water nitrate risk management [J]. Water Resources Research, 1994,30:135–148.
[6] Kumar G, Maiti J. Modeling risk based maintenance using fuzzy analyticnetwork process [J]. Expert Systems with Applications, 2012,39:9946–9954.
[7] Goodrich M T, McCord J T. Quantification of uncertainty inexposure assessments at hazardous waste sites [J]. Ground Water, 1995,33(5):727–732.
[8] Hamed M M, Bedient P B. On the performance of computationalmethods for the assessment of risk from groundwater contamination [J]. Ground Water, 1997,35(4):638–646.
[9] Batchelor B, Valde´s J, Araganth V. Stochastic risk assessment ofsites contaminated by hazardous wastes [J]. Journal of Environmental Engineering, 1998,124:380–388.
[10] Guyonnet D, Bourgine B, Dubois D, et al. Hybrid approach for addressing uncertainty in riskassessments [J]. Journal of Environmental Engineering, 2003,129:68–78.
[11] Li J B, Huang G H, Chakma A, et al. Integratedfuzzy-stochastic modeling of petroleum contamination in subsurface [J]. Energy Sources. 2003,25:547–563.
[12] Hu Y, Wen J Y, et al. A dynamic multimedia fuzzy-stochastic integrated environmentalrisk assessment approach for contaminated sites management [J]. Journal of Hazardous Materials, 2013,261:522-533.
[13] 金菊良,吴开亚,李如忠.水环境风险评价的随机模拟与三角模糊数耦合模型 [J]. 水利学报, 2008,39(11):1257-1261.
[14] Destouni G. Predicting uncertainty in solute flux throughheterogeneous soil [J]. Water Resources Research, 1992, 28:793–802.
[15] Blair A N, Ayyub B M, Bender W J. Fuzzy stochastic risk-baseddecision analysis with the mobile offshore base as a case study [J]. Marine Structures, 2001,14:69–88.
[16] Arunraj N S, Maiti J. A methodology for overall consequence modelling inchemical industries [J]. Journal of Hazardous Materials, 2009,169(1–3):556–574.
[17] Van der Pas J W, Marchau V A, Walker W E, et al. ISA implementation and uncertainty: a literature review and expertelicitation study [J]. Accident Analysis and Prevention, 2012,48:83–96.
[18] 李跃清,王文圣,金菊良.水文水资源随机模拟技术 [R]. 成都:四川大学出版社, 2007.
[19] 何 丹,马东豪,张锡洲,等.土壤入渗特性的空间变异规律及其变异源 [J]. 水科学进展, 2013,34(3):340-347.
[20] 徐 亚,颜湘华,董路等.基于Landsim的填埋场长期渗漏的污染风险评价 [J]. 中国环境科学, 2014,34(5):1355-1360.
[21] GB/T22105—2008,土壤质量总汞、总砷、总铅的测定原子荧光法 [S]. 2008.
[22] 谌宏伟,陈鸿汉,刘 菲,等.污染场地健康风险评价的实例研究[J]. 地学前缘, 2006,(1):230-235
[23] Hsiao H W, Susanne M U, Trevor W T. Burdens of mercury in residents of Temirtau, Kazakhstan: II: Verification of methodologies for estimating human exposure to high levels of Hg pollution in the environment [J]. Science of The Total Environment, 2010,408(19):4033–4044
A fuzzy-stochastic integrated model of contaminated site risk assessment model and case study.
XU Ya, ZHU Xue-mei*, LIU Yu-qiang, NAI Chang-xin, DONG Lu
(Chinese Research Academy of Environmental Sciences, Beijing 100012, China). China Environmental Science, 2014,34(10):2692~2700
Risk assessment is associated with uncertainties in nature, and neglect of those uncertain elements in evaluating risk will inevitably lead to difficulty for decision-makers in the stage of risk management and decision-making. Fuzzy theory was used to describe the fuzzy uncertainties, and probability theory was employed to describe the random uncertainties. A coupled fuzzy-stochastic model was built to resolve the problem of complex computation of fuzzy numbers in which fuzzy number are represented with the function of uniform random variables. Monte Carlo method was also used to simulate the computation between fuzzy numbers. One mercury contaminated site located in Qinghai Province was selected as a case to demonstrate the effectiveness and reasonability of this coupled model. The reasonability of this model was verified by comparing simulated results of the widely used RBCA model. The case study indicated that: 1) the main exposure pathway was oral intake with a contribution rate of 80%; 2) the health risk of this contaminated site was acceptable with non-carcinogenic Hazard Quotient (HQ) of 0.28 under normal exposure condition; under the most unfavorable exposure condition which appearance probability was less than 1%, the health risk was unacceptable with HQ equals to 1.28; 3) the health risk would decline in time and reach to an acceptable level after about six years. Therefore, it was suggested that the related responsibility should provide other drinking water resources to eliminate the exposure routine in the period of the first 6 years or the 6-8 years rather than take engineering measurements to remediate this contaminated site.
t:fuzzy-stochastic;exposure assessment;uncertainties;risk assessment
X820.4
:A
:1000-6923(2014)10-2692-09
徐 亚(1985-),男,湖南岳阳人,助理研究员,博士生,主要从事固体废物管理和环境风险评价工作.发表论文10余篇.
2013-11-08
国家环境保护公益性行业科研专项(201209022);2012年度院所基本科研业务专项(2012YSKY16)
* 责任作者, 副研究员, zhuxm@craes.org.cn

