基于动态Terminal滑模控制的无刷直流电机系统研究
苗敬利,邹 靖
(河北工程大学 信息与电气工程学院,邯郸 056038)
基于动态Terminal滑模控制的无刷直流电机系统研究
苗敬利,邹 靖
(河北工程大学 信息与电气工程学院,邯郸 056038)
0 引言
无刷直流电机(BLDCM)因其可靠性高、体积小、控制精度好等优越性能,被广泛应用于生活的各个领域[1,2]。随着其应用的不断扩展,对其控制性能要求也越来越高,传统的速度控制器中主要采用的是PID控制算法,在系统的快速性、抗干扰能力和对负载变化的适应能力上不够理想,从而很难达到闭环系统要求的动静态性能指标。滑模变结构控制与传统PID控制相比,其算法简单、易于实现,并且不受受控系统参数变化和噪声干扰的影响,故具有良好的非线性跟踪特性和更强的鲁棒性,是解决非线性问题的重要方法[3,4]。本文以二相导通三相星型连接无刷直流电机为研究对象,设计一种动态Terminal滑模控制器,并利用Lyapunov函数证明其稳定性,使系统状态在有限的时间内收敛至平衡点,提高控制效果[5]。
1 无刷直流电机(BLDCM)的数学模型
无刷直流电机三相定子绕组的平衡方程:
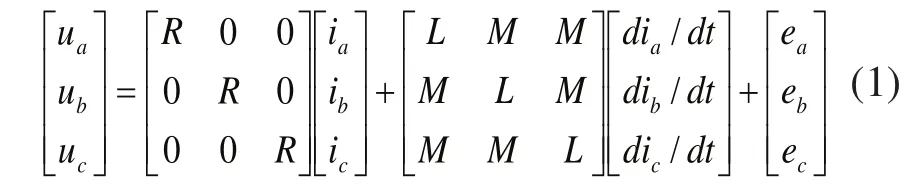
其中:ua、ub、uc为三相定子绕组电压;ia、ib、ic为三相定子绕组电流;r:定子电阻;L:定子相自感;M:定子相互感;ea、eb、ec为定子各相反电势。
本文假设电机三相绕组Y型对称连接,并且没有中线,在忽略电机铁心饱和,不计涡流损耗和磁滞损耗的情况下分析数学模型及电磁转矩等特性。则有:
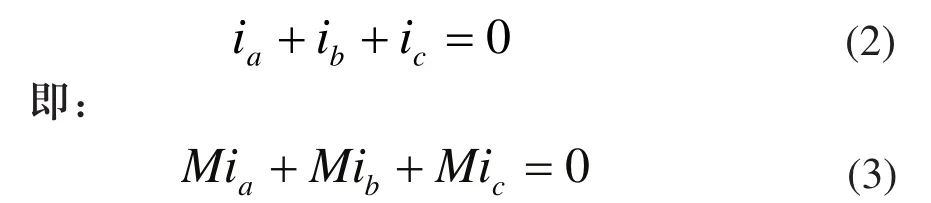
将式(2)与式(3)代入式(1),可变为:
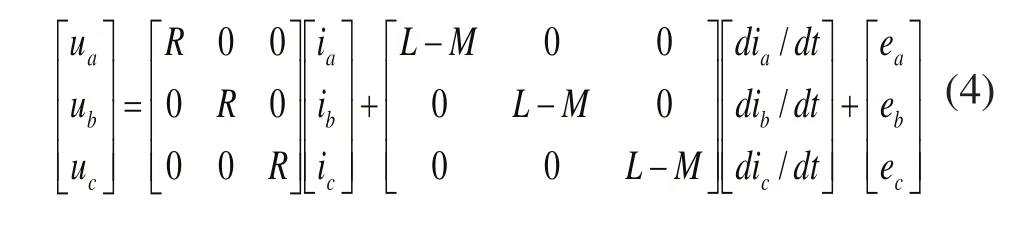
无刷直流电机(BLDCM)的转矩方程:
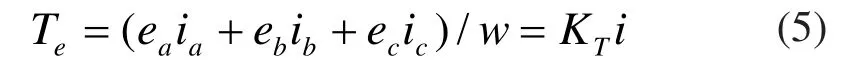
电机的运动方程:
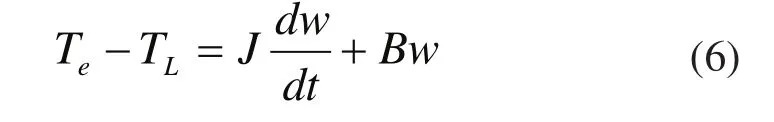
其中:Te为电磁转矩;TL为负载转矩;J为转动惯量;B为摩擦系数;w为机械转速。
2 动态Terminal滑膜控制器设计
2.1 动态Terminal滑膜变结构的原理
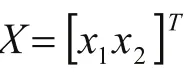
系统描述为:
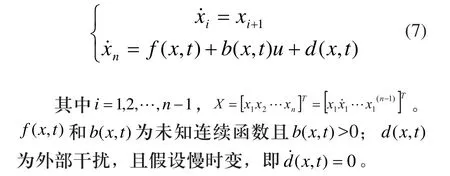
2.2 无刷直流电机的动态Terminal滑膜控制器设计
由式(3)和式(4)可推出:
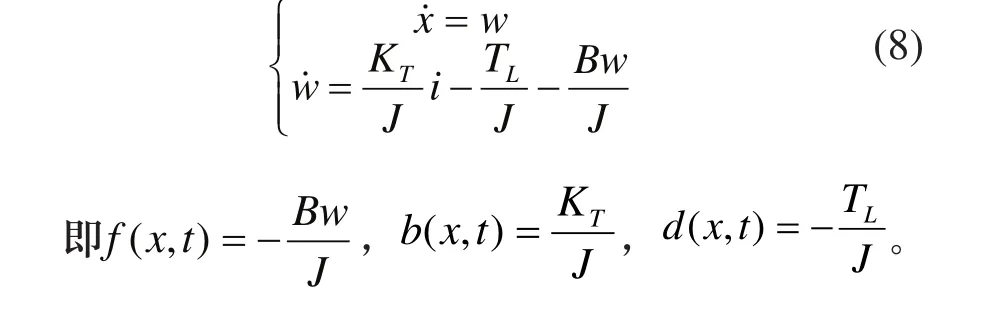
定义控制系统的跟踪误差为:

定义动态Terminal滑动模面为:
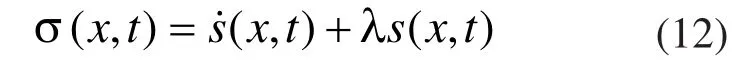
其中λ为正的常数。
系统稳定性分析:
定义Lyapunov函数:
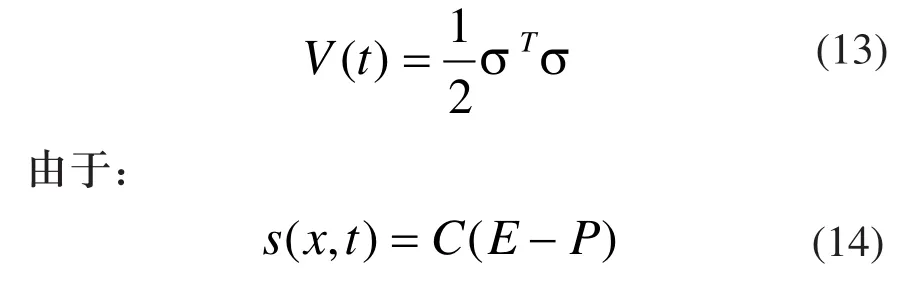

设计动态滑模控制律为:
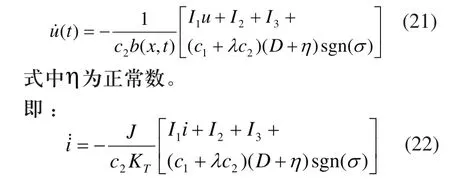
将式(17)代入式(14),整理得:
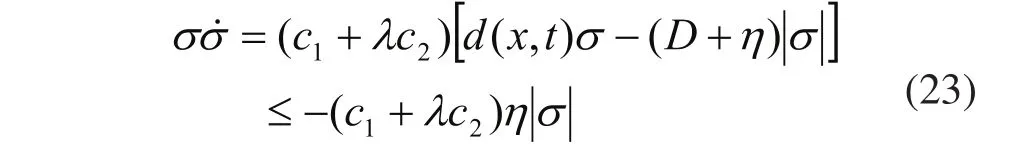
2.3 基于动态Terminal滑模变结构控制算法的仿真分析
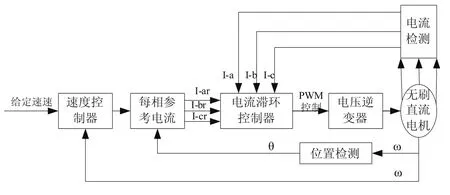
图1 基于动态Terminal滑模变结构控制算法的无刷直流电机控制系统模型
3 系统仿真与实验结果

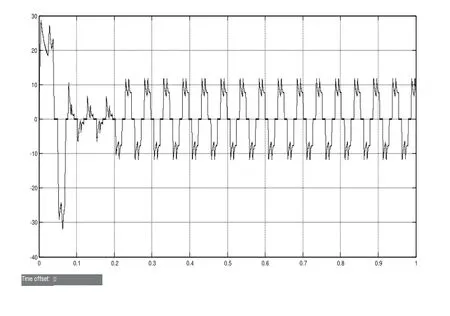
图2 a相电流响应曲线
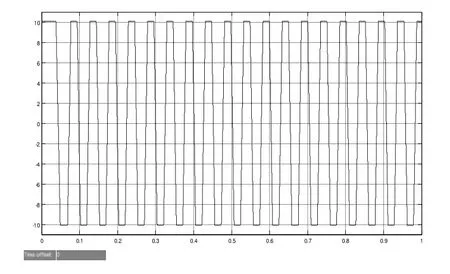
图3 a相反电势响应曲线
由以上仿真图可知,实际波形与理论波形基本上保持一致,证明了该控制算法可行,且具有良好的动静态性能,能保证系统稳定运行,验证了仿真模型的正确性和可行性。
下面将该控制算法与传统的PID控制算法相比较,所选用的PID控制器参数设定为:Kp=5,Kd=0.001,Ki=0.01。所得的仿真曲线如图4~图5所示。
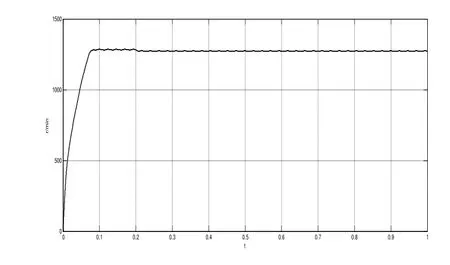
图4 动态Terminal滑模控制速度响应曲线
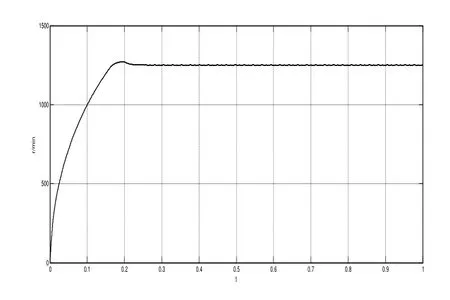
图5 传统PI控制速度响应曲线
本文利用了MATLAB/Simulink对无刷直流电机控制系统进行了仿真实验分析,得到了应用了动态Terminal滑模控制后的仿真图形,证明该算法可消除切换函数引起的抖振,确保了在有限时间内使系统状态收敛为零。并且将此控制算法与传统的PID控制算法比较,证明了通过动态Terminal滑模控制算法对速度控制器的调节,使整个闭环系统具有更好的快速性,跟踪精度高,达到了要求的控制精度。
4 结束语
针对传统电机速度控制器存在的跟踪精度差和收敛性行不够的特点,本文综合了Terminal滑模控制的收敛性和动态滑模的快速稳定性,设计了由动态Terminal滑模控制算法调节的无刷直流电机速度控制器,确保跟踪误差在有限时间内收敛至零的前提下使整个闭环系统有个更好的鲁棒性和动静态性能指标。从仿真结果上看,改控制算法也提高了系统的控制精度,消除了抖振,具有实际的应用价值。
[1]夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009:1-15.
[2]Yu Liu, Chen Guo,Jin Lv. Adaptive Nonlinear Backstepping Sliding Mode Control for Ship Course Tracking[J].Proceedings of the 4th International Conference on Impulsive and Hybrid Dynamical Systems,2007,1547-1551.
[3]贾洪平,魏海峰.无刷直流电机滑模变结构电流控制[J].微电机,2010;43(2):58-61.
[4]刘金琨.滑模变结构控制MATLAB仿真[M].北京:清华大学出版社,2005:333-360.
[5]雷晓犇,陈卓,熊攀,谭海军.基于模糊动态Terminal滑模的永磁同步电机控制研究[J].空军工程大学学报.2012(13):6-10.
Research about a system of the brushless DC motor based on dynamic Terminal sliding mode control
MIAO Jing-li, ZOU Jing
无刷直流电机(BLDCM)由于具有结构简单、效率高、维护方便等优点,因此得到了广泛的应用。但在其工作过程中,易受到外部干扰、参数摄动等因素的影响。针对这一问题,本文引入了动态Terminal滑模控制器,可使系统状态在有限时间内收敛为零,突破了普通滑模控制在线性滑模面条件下状态渐进收敛的特点。仿真结果表明所用控制算法提高了系统的稳态跟踪精度,对参数变化不敏感且鲁棒性好,使整个闭环系统满足期望的动静态性能指标。
无刷直流电机;滑模变结构控制;闭环控制系统;抖振
苗敬利(1967 -),女,副教授,博士,主要研究方向电力电子与电力传动、非线性控制。
TM3
A
1009-0134(2014)06(上)-0061-03
10.3969/j.issn.1009-0134.2014.06(上).17
2014-01-02

