一种圆柱通道型橡胶反声障板的研究
边汉林 夏铁坚
(1.海军青岛雷达声纳修理厂,青岛,266100;2.第七一五研究所,杭州,310012)
反声障板是声呐水下系统的重要部件之一,它具有反声、隔声和去耦等功能,可改变声基阵的指向性参数,提高接收或发射的空间增益,其性能往往直接影响到声呐水下声系统的技术指标。反声障板的研究一直以来受到人们的重视,有多家单位采用不同材料和方法研制各种反声障板,以满足声呐设备水下声系统的研制需求[1]。天津橡胶研究所对一种将聚氨酯泡沫进行预压缩处理后形成的耐压反声障板进行了研究。中国科学院声学研究所对钢板空气腔障板进行了研究,以满足低频反声性能的需求。本文对一种通道型橡胶反声障板进行了研究。该反声障板的主要基材为橡胶,橡胶具有一定的强度,可以承受一定的压力;同时,它又有粘弹性,可以产生迟滞损耗和较大的弹性形变。由橡胶制成的具有圆柱通道的层状结构,是一种可以确保在宽频带、宽静水压范围具有良好反声性能的声学障板[2]。
这种障板有效工作的物理机理在于:橡胶的体积模量和水的体积模量大致相当,但它的剪切模量比体积模量小两个数量级;因此可以通过将体积形变转化为剪切形变的方法来降低障板的有效压缩模量,从而降低声速。一种形变向另一种形变的转换是通过在实心材料内制造空气腔或者通道来实现的。此时,声波透入障板产生的相对较小的体积形变会引起较大的剪切形变,可以降低障板的表观声速和特性阻抗,从而实现障板的反声效果。
1 障板声学性能估算
带有圆柱通道的橡胶障板模型如图1所示,其中a为管的内半径,b为管的外半径,h为管的高度,p为作用于圆柱管端面的压力。
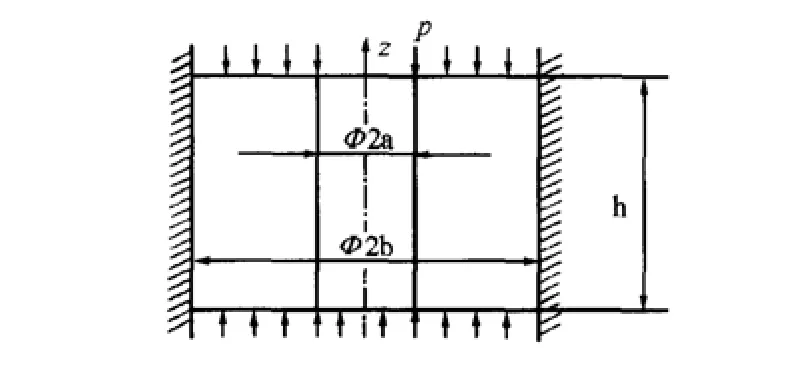
图1 带圆柱通道的橡胶反声障板模型
对于该问题的精确分析涉及到求解波数k的繁杂的超越方程[3],我们采取了一种“静态”的近似分析方法,求解简单,物理意义明确。当腔体尺寸远小于材料弹性波的波长时,用该方法来分析带有圆柱通道的橡胶障板是具有较好精度的[4-5]。
圆柱的轴对称振动方程可以表示为:
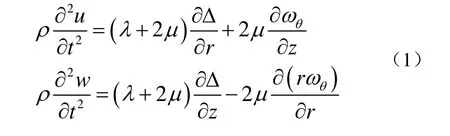
假设压缩力作用于通道的端面,通道的形变是轴对称的,并且是平面的。方程(1)可以转换为如下的平衡方程:
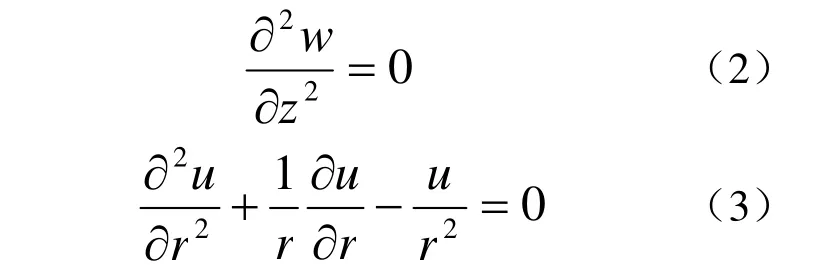
沿z轴的相对形变值δ是方程(2)的解为:
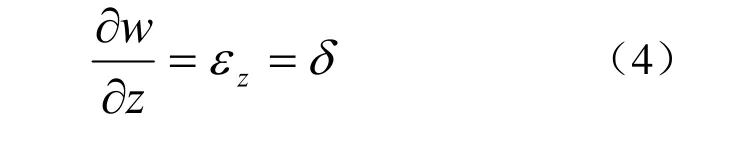
方程(3)是二阶线性欧拉方程。由于圆柱通道在障板内呈周期性分布,考虑声波垂直入射时,可以采取如下边界条件:当r=b时,u= 0;当r=a时,σr= 0。其中σr为径向应力。可以确定径向位移分布为:

其中,ε2=a2/b2为穿孔系数。
通道的等效弹性模量定义为:

其中,p为作用在整个端面上的压力(作用在整个封口橡胶板上),如图 1所示。通道横截面应力σz与p之间的关系可以表示为:
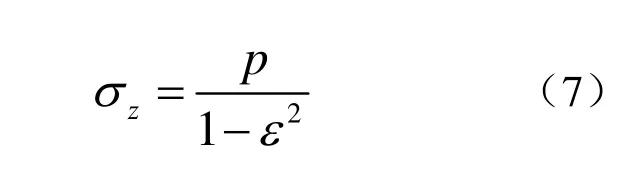
当μ<<λ,μ<<λε2成立时,联合(5)、(6)和(7)可以得到带通道的橡胶障板的等效弹性模量和声速,表示为:

带有通道的橡胶障板的等效密度可以表示为:
(3)上级财政专项下达较晚。厦门T大学的市级财政专项一般年初就随着预算下达,但是省专项、中央专项的下达时间一般都在8月份之后,有些甚至年底才到账,当年项目执行时间就比较短,执行进度也比较慢。
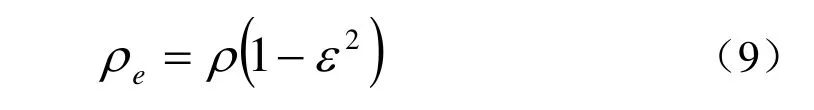
2 高静水压下障板声学性能估算
声学障板在舰船上工作时,常常需要评估其在高静水压环境下的性能。当障板处在高静水压下时,其内部的通道会被压缩,声学性能会有一定程度的下降。
假定通道被压缩时,形状保持不变,即沿z轴的相对形变δ在通道的所有截面上沿高度方向都是一样的,而径向位移u与z无关,如图2所示。于是可以得到:
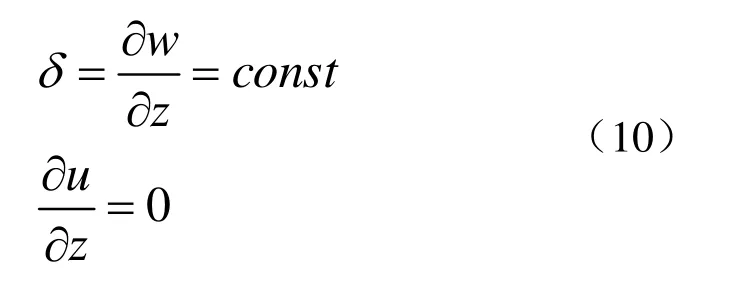
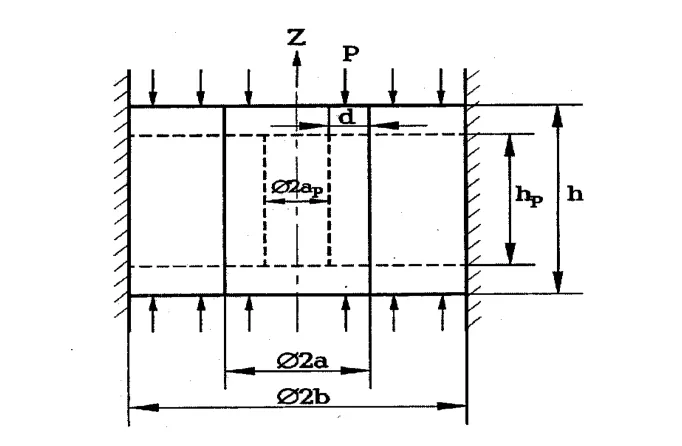
图2 高静水压下的圆柱通道橡胶反声障板模型
这样,可以应用线性弹性理论的关系来计算压缩状态下通道的弹性模量。在求解该问题时,我们假定通道的形变是线性的。此时,压力p和在其作用下产生相对形变δ的关系可以表示为:

其中,Eep为在压力p下通道的模量,其可以表示为:
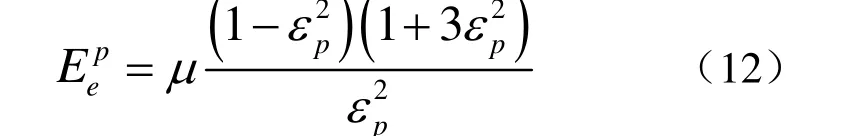

其中,V0和Vp分别表示为初始的橡胶体体积和压缩后的橡胶体体积,可以表示为:

由公式(14)和(15)可以得到:

由公式(11)、(12)和(16)可以得到:
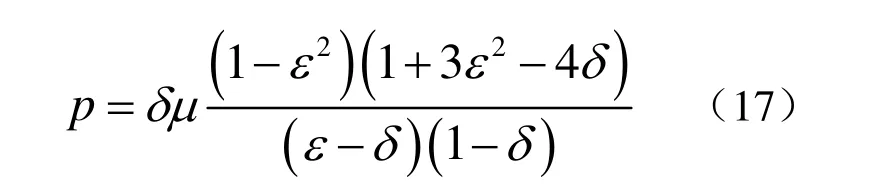
从而可以得到橡胶反声障板圆柱通道的压缩曲线,如图3所示。通道的模量Eep的值为压缩曲线的切线值,通过横坐标轴在p点与压缩曲线切线的倾角来确定,即:

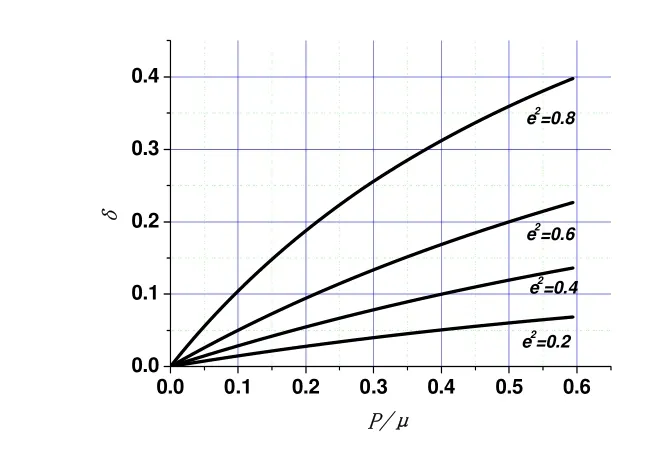
图3 圆柱通道的压缩曲线
3 实验分析
在上述理论分析的基础上,实际制作了通道型橡胶反声障板。障板采用丁苯橡胶材料制作。利用动态分析仪对丁苯橡胶的剪切波进行测量。在 20℃时,测得剪切波的速度为80 m/s。障板由5层复合而成,如图4左侧所示。5层中,有3层为实心橡胶层,2层为带通道结构的橡胶层,这5层通过硫化粘接在一起。其中实心层主要用于对带通道结构橡胶层的水密,防止水介质进入到空气通道中。每层实心橡胶层的厚度为5 mm。障板的反声性能主要由带通道结构的层来实现的,如图4右侧所示。该层的设计参数为:穿孔系数为 0.6,b/h=0.5。该层厚度为7 mm。这样整个障板的厚度为29 mm。
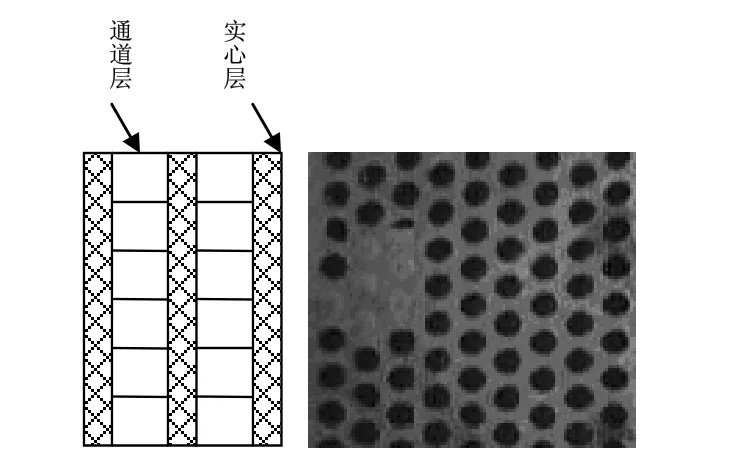
图4 障板示意图及通道层
障板上安装的水听器采用直径为 30 mm的球形水听器,如图5所示。为使水听器安装方便,在声学障板上留有水听器的安装孔。水听器上的支撑结构和电缆可以穿过该安装孔进行安装、固定。为了保证水听器在较宽的频带范围内具有较平坦的响应,经过优化,取水听器中心与声障板之间的距离为40 mm。

图5 带障板的水听器
水听器带障板以后的灵敏度如图6所示。图中实线是按第1节理论计算的结果,带点的线为实际测量的值。从图中可以看出两者吻合较好,充分说明利用第1节中近似公式计算在常压下的声障板性能具有比较好的精度。
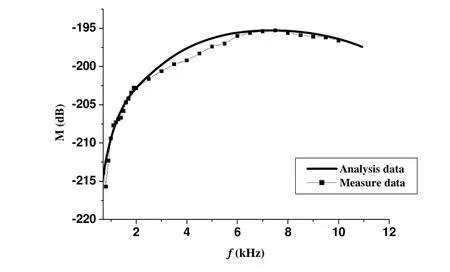
图6 常压下带障板水听器的灵敏度
图7给出的是在2 MPa静水压力下水听器的灵敏度。图中实线为按第2节理论计算的结果,带点线为实际测量的结果。为便于比较,在水听器灵敏度中将水听器自身由于静水压力增加而导致灵敏度下降那部分进行了扣除。从图中可以看出,在高静水压情况下,水听器灵敏度理论计算值与实际测量值之间存在一定的偏差。
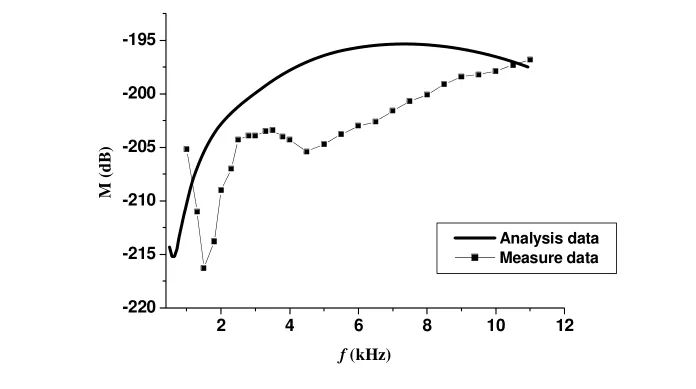
图7 2 MPa下带障板水听器灵敏度
随着静水压力的增加,水听器在频带范围内的灵敏度极小值逐渐向高频移动。理论计算曲线和实际测量结果都显示了这样的趋势。但在实际测量的曲线中,由于静水压力引起障板声学性能的下降比理论计算要严重。无论从水听器灵敏度极小值往高频方向移动,还是带障板水听器灵敏度的下降,实际测量比理论计算严重。主要原因是在高静水压下,障板中橡胶通道的形变为非线性形变。而在本文的计算模型中是假定橡胶通道的形变是线性的,两者存在一定的差别。
4 结论
通过上述分析,可以得出以下结论:1)文中建立一个“静态”近似模型对带圆柱通道的橡胶障板的声学性能进行了计算,给出了障板的等效声速和密度,并且对障板上水听器灵敏度进行了理论分析与实际测量,两者较为一致。
2)建立了高静水压下圆柱通道橡胶障板的理论计算模型。以此为基础,对高静水压下带障板水听器的灵敏度进行了计算,并与实测值进行了比较。理论结果较好地预测了静水压增加时,带障板水听器灵敏度的变化趋势。但在频带范围内的灵敏度极小值,以及静水压引起灵敏度下降等方面,理论与实测还存在一定的差别。
3 )造成这种差别的原因是在理论分析模型中,假定在高静水压下,橡胶通道的形变是线性的,而在实际情况中形变是非线性的。需要在模型中加以修正。
[1]耿成德. 耐压反声障板特性及其对水听器指向性的影响[J]. 声学与电子工程, 1989, (2):7-10.
[2] 张德志, 周利生, 翁志学, 等. 圆柱形通道结构橡胶声障板[J]. 应用声学, 2004, 23(2):45-48.
[3] 何世平,汤渭霖,何琳,等. 变截面园柱形空腔覆盖层吸声系数的二维近似解[J]. 船舶力学,2006,10(1):120-127.
[4] GAUNAURD G C. One-dimensional model for acoustic absorption in a viscoelastic medium containing short cylindrical cavities[J]. Journal of Acoustical Society of America, 1977, 62(2):298-307.
[5] 朱蓓丽,任克明. 等效参数法研究带圆柱通道橡胶体的声学性能[J]. 上海交通大学学报, 1997, 31(7):20-25.

