基于FPGA实现CT图像重建加速的设计

张晓梦，张 涛

（1.中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033；2.中国科学院大学，北京 100049；3.中国科学院 苏州生物医学工程技术研究所，江苏 苏州 215163）

1 引 言

目前CT系统都需要将DAS（数据采集系统）采集的投影数据传输至工作站中进行重建，随着CT技术的发展，采集到的数据量越来越大，这不仅增加了数据传输的时间，而且对滑环等部件也提出了更高的要求。如果在CT的DAS中嵌入图像重建系统，在传输前对投影数据进行重建处理，可有效减少传输压力。但是这对图像重建系统的实时性有很高的要求，并且系统要具有体积小，功耗低的特点。

该重建系统可利用ASIC（Application Specific Integrated Circuit）、DSP［1］（Digital Signal Processor）、GPU［2］（Graphic Processing Unit）等硬件实现。ASIC处理速度快，适合高性能计算加速，但一经设计，功能便不再改变，不易于升级和维护，且开发难度较大；DSP芯片的高速信号处理能力可以快速实现算法，但它的并行结构需要拓展多块DSP来实现［3］；GPU适用于并行计算来提高重建速度，但它不能独立完成运算处理，需要CPU提供执行指令。

针对上述问题，本文提出了一种基于FPGA实现CT图像重建的方法，在FPGA上设计了多通道并行流水线的处理结构。与其他硬件技术［3］相比较，利用FPGA设计的重建系统采用全数据流的形式处理数据，脱离了指令操作，在处理速度上大大增加；采用模块化设计方法，可根据算法需要配置内部逻辑功能，方便修改和维护；重建电路集成在FPGA上实现，体积小，功耗低，可嵌入CT设备中实现高性能的图像重建。

2 算法原理及并行处理结构

2.1 FBP算法［4］

FBP算法是以中心切片定理为基础。该定理将二维图像与其一维的投影数据在傅里叶域中联系起来。中心切片定理的原理如图1所示。

设F（μ，v）是图像函数f（x，y）的二维傅里叶变换。根据该定理，当投影数目足够多时，原图像可由傅里叶逆变换获得重建：

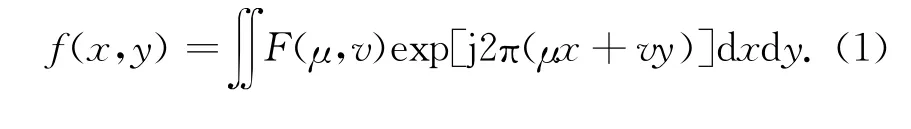
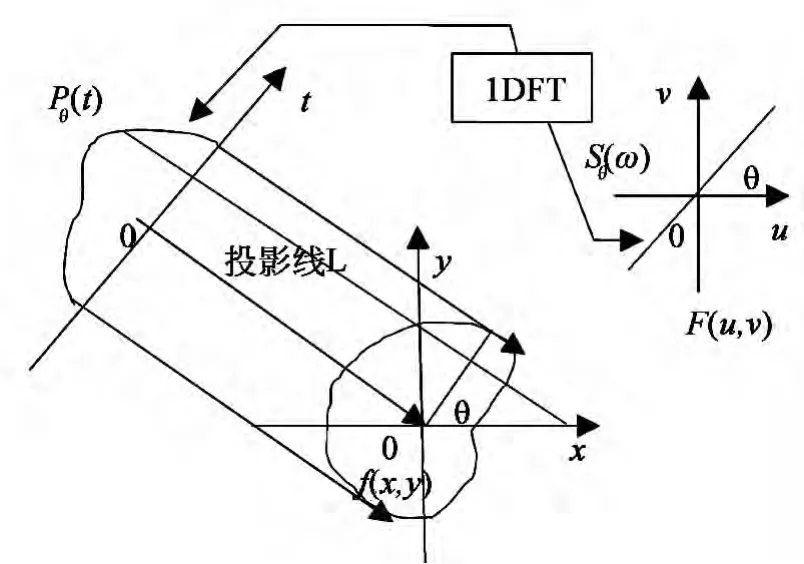
图1 中心切片定理原理图Fig.1 Principle diagram of slice theorem

直接反投影会造成边缘模糊现象，为消除这种现象，反投影前需对投影数据进行低通滤波，这就是FBP算法。算法公式为：

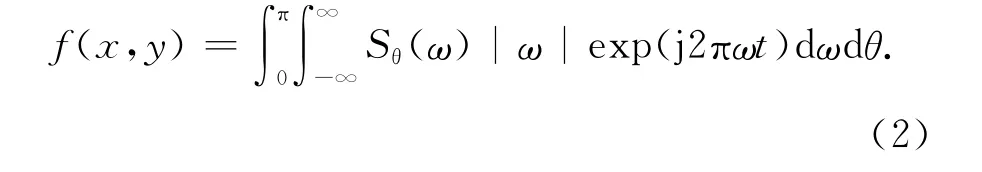
为方便在FPGA上的实现，将算法分为以下步骤处理：

（1）对投影数据投影角度进行滤波。

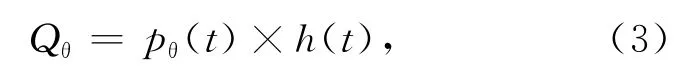
其中：h（t）为斜坡滤波函数，频率响应为｜ω｜。

（2）将滤波后数据进行反投影计算。

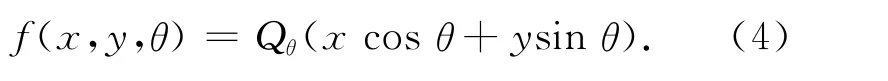
反投影计算采用线性插值实现。

（3）将各投影角度下反投影结果累加

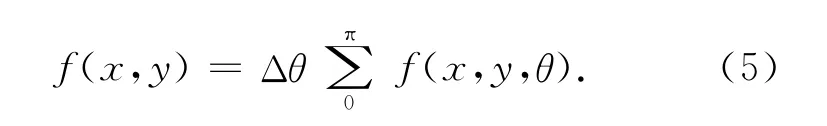
2.2 FBP算法的并行结构

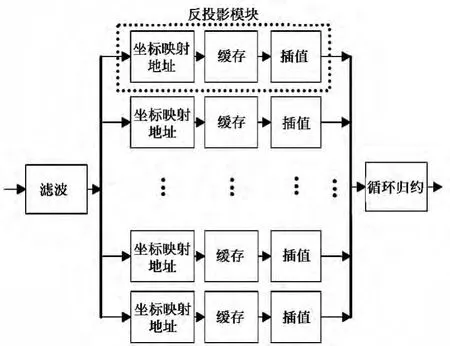
图2 FBP算法的并行处理结构Fig.2 Parallel processing structure of FBP algorithm

实际中，不同分度下的投影数据互不相关，并且不同分度下FBP算法的计算过程也是重复且不相关的，可同时进行多个分度下的重建计算。基于这种并行性，实现算法加速的关键技术在于多通道并行计算策略。重建过程中，反投影部分计算量最大，考虑实际的逻辑资源占用，本文采用将投影数据串行滤波后再并行反投影的处理结构。

3 数据结构

由于可编程逻辑电路的结构特点，FPGA内部采用定点化的运算方式，运算的数据类型需统一量化为定点型。

数据的定点化需要平衡精度和资源占用之间的矛盾。本文采用Leeser提出的分级定点化的数据结构［5］，将不同阶段的数据量化成为不同长度：原始数据量化为10位有符号定点数，滤波后数据量化为9位有符号定点数，反投影阶段的插值因子量化为4位无符号定点数，最后重建结果量化为9位有符号定点数。此种量化方式能够在相对误差较小的情况下，减小资源占用。仿真实验验证，重建结果的相对误差小于0.004。

4 主要功能模块的设计

在FPGA上实现的重建加速系统主要包括滤波单元、反投影单元和循环累加单元3部分。

4.1 滤波单元

滤波模块用于对投影数据的卷积滤波，卷积公式为：

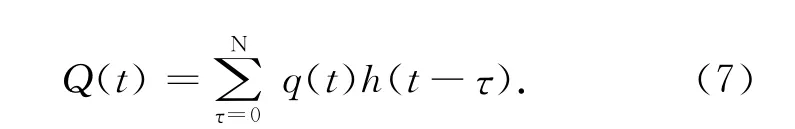
由上文可知滤波函数的频域表示为H（ω）＝｜ω｜。这里我们将其转换为121阶对称斜坡FIR滤波器［4］，抽头系数为：

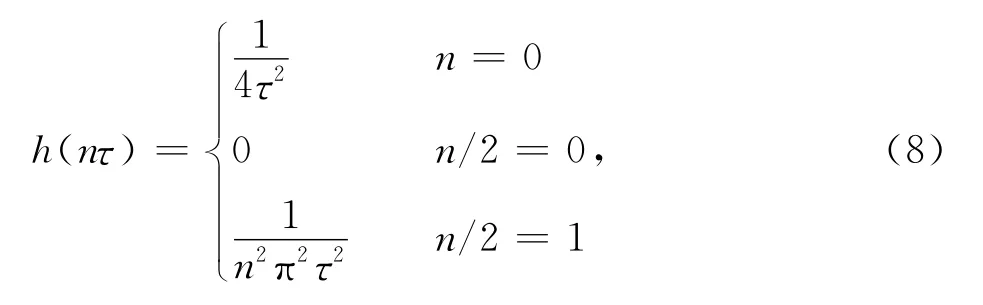
其中：τ为投影数据的采样间隔。

有效利用Altera提供的FIR IP核实现这一功能，以减小设计难度。由于滤波时投影数据连续串行进入滤波器进行处理，为了避免各投影角度之间卷积发生混叠，每输入一行数据，需进行补零操作，补零的长度为滤波器阶数。

4.2 反投影单元

反投影单元是系统的核心部分，为提高处理速度，对反投影过程采用流水线设计，在处理过程中可实现一个时钟周期更新一个重建点的速度。

反投影过程的实现分为4个步骤：首先根据坐标间映射关系确定重建像素点在探测器上的地址；然后由前级结果计算缓存地址；再按地址从缓存中读出数据；最后数据进入插值单元进行插值计算得到反投影结果。图3给出了单条反投影单元的结构框图。

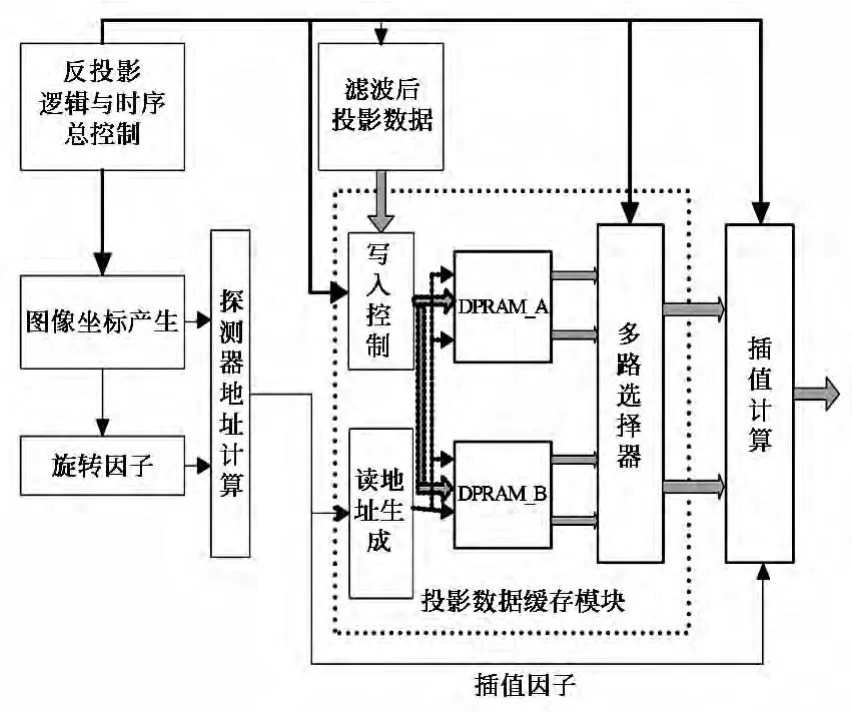
图3 FPGA实现反投影的系统结构Fig.3 System block diagram of back－projection by FPGA

4.2.1 地址计算模块

地址计算模块用于计算探测器坐标与图像坐标的映射关系，计算公式为式（3）中t的计算。电路实现过程为：两个计数器完成重建点坐标（x，y）的循环，与旋转因子模块的读出数据同时输入探测器坐标计算单元，进行坐标计算，结果的整数部分作为探测器地址；小数部分则作为插值因子输出。

旋转因子是各投影角度对应的正弦、余弦函数的值，在FPGA内直接利用计算十分复杂，因此，可利用查找表（look up table，LUT）方式获得，牺牲一定的存储空间，可大幅提高处理速度。为避免数据的重复，ROM中只保存余弦函数值，正弦函数值通过逻辑变换得到，可节省50%的存储空间。

4.2.2 缓存模块

流水线的缓存模块采用可乒乓循环的双缓存组结构［6］。每组缓存都由一块片上双口RAM组成，当读地址为addr时，同时输出地址为addr和addr＋1的两个相邻的滤波后投影数据。在反投影处理过程中，一块缓存写入数据，同时另一块缓存读出数据到下一单元进行插值计算。一个分度下所有像素点的反投影处理完成后，互换读写状态，完成一次乒乓循环，单条流水线缓存单元的读写控制如图4所示。

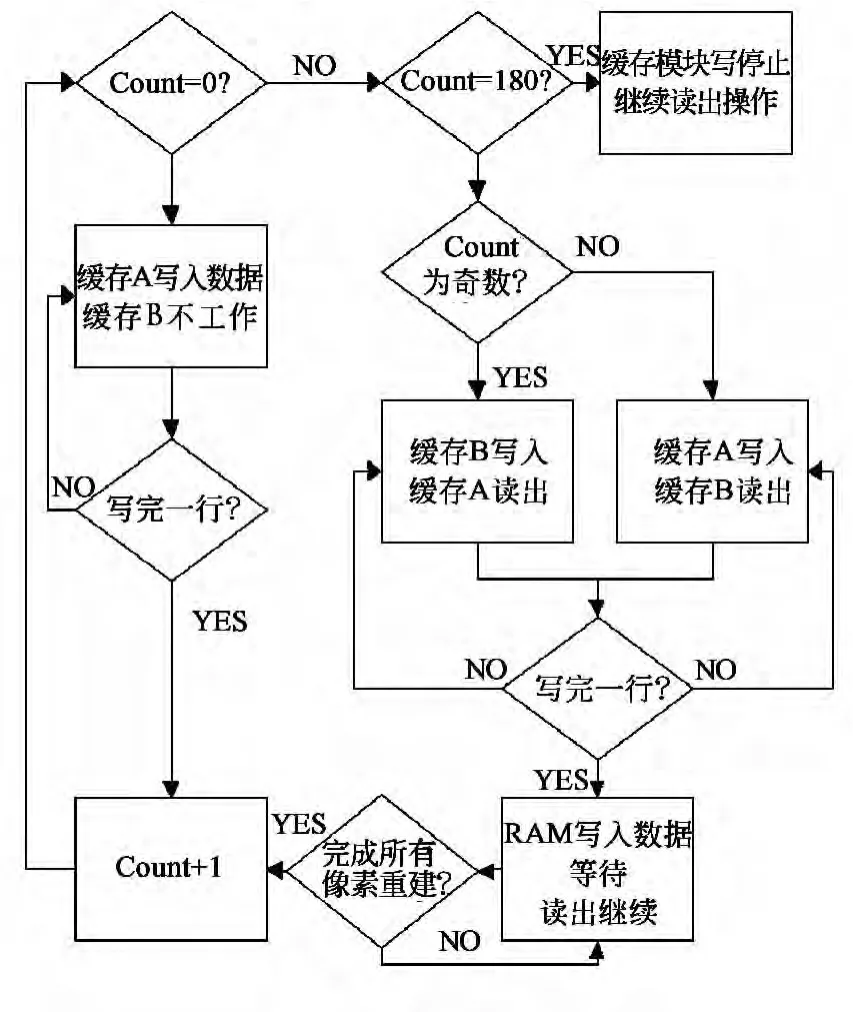
图4 双缓存组的读写控制流程Fig.4 Control flow of double buffers

采用这种片上数据缓存结构，一个时钟周期内，坐标计算单元更新一个地址数据，缓存单元输出插值所需的两个数据；乒乓循环机制避免了预存占用时间，无需等待便可继续进行反投影操作，大大提高了系统的处理效率［7－9］。

4.2.3 插值计算模块

插值计算公式为：

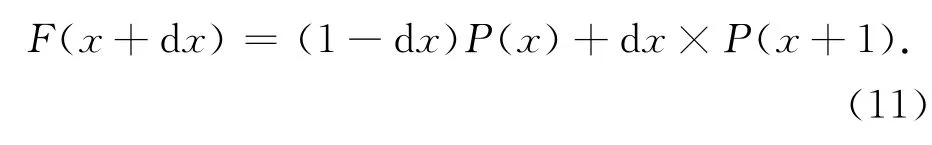
将其改写为：

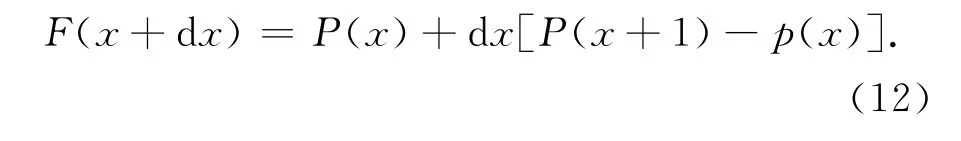
可减少一个乘法器的使用［10］。具有流水线特性的电路结构为：

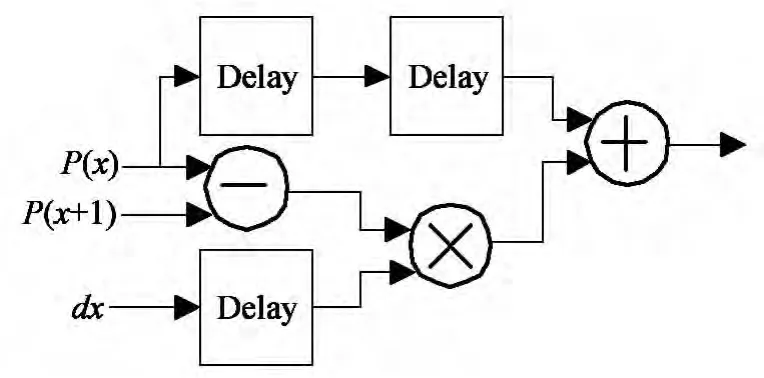
图5 线性插值计算单元Fig.5 Computing unit of linear interpolation

4.2.4 控制模块

反投影逻辑与时序总控制控制模块通过状态机生成控制信号，实现对反投影流水线各模块的控制，使各模块按照一定的时序完成功能，保证数据按流水线进行处理。

4.3 反投影单元并行流水线

重建一幅N×N的图像，一个投影分度下的滤波后数据的预存需N／2个时钟周期，反投影处理需N2个时钟周期，预存所需时间远远小于反投影所需时间，所以并行流水线时，数据的预存过程采用顺序结构，通过数据接口选择控制单元来将数据输入对应流水线。

若采用n条反投影流水线并行处理，那么重建一幅M×N2（M为投影角度数）的图像，反投影计算只需个时钟周期，反投影速度与并行流水线个数成正比。

4.4 循环累加单元

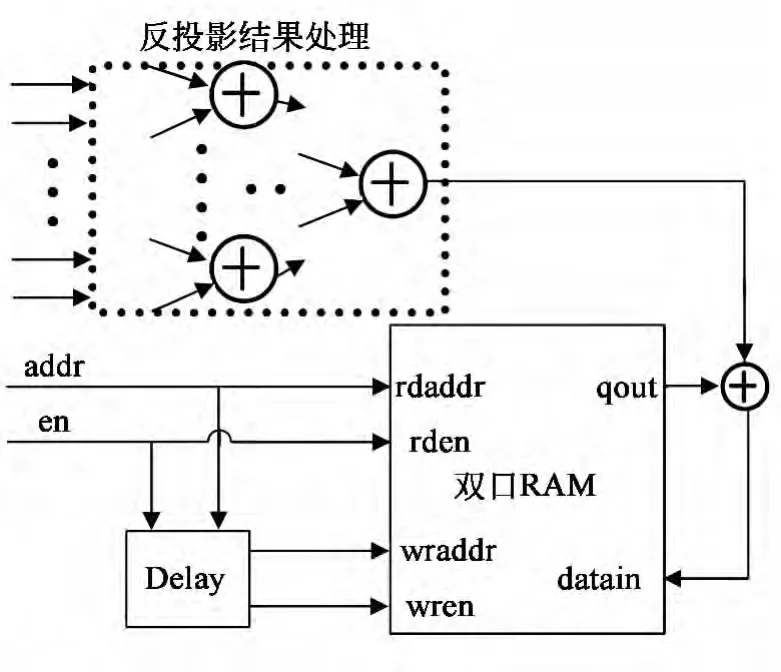
图6 循环累加单元Fig.6 Cycle accumulate unit

由于FPGA内部资源的限制，反投影流水线的个数受限，很难达到所有投影角度同时并行处理，所以，需要对每一次的并行处理结果进行存储以完成累加。并行处理结果相加后输入循环累加单元，与存储器中对应地址的数据进行相加，结果写入原地址，直到所有角度下投影处理完毕，将重建结果输出。循环累加单元可利用一块双口RAM实现读写操作的同时进行。

5 仿真结果与分析

本文设计为12条流水线并行处理结构，采用分级定点化方式［3］，根据上述各功能模块的设计，并在相关平台上进行仿真实验，验证加速效果。

图7为shepp－logan标准体模的投影重建；图8为脑部CT图像的投影重建。由重建结果可以看出，FPGA重建图像边缘清晰，细节完整，肉眼观察时与CPU重建图像效果相差极小。将CPU重建图像与FPGA重建图像对应像素点相减取绝对值，绝对误差小于0.004，精度损失很小。

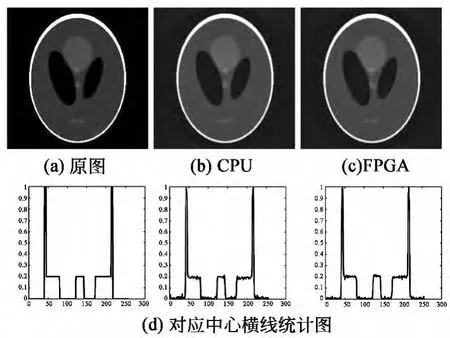
图7 shepp－logan重建结果对比Fig.7 Reconstruction result of shepp－logan

仿真实验中，FPGA时钟频率取100MHz；计算机CPU 为Intel（R）Core（TM）i5－2400 3.10 GHz，内存为4GB。表1给出FPGA与CPU分别对不同规模投影数据进行重建时的速度对比。

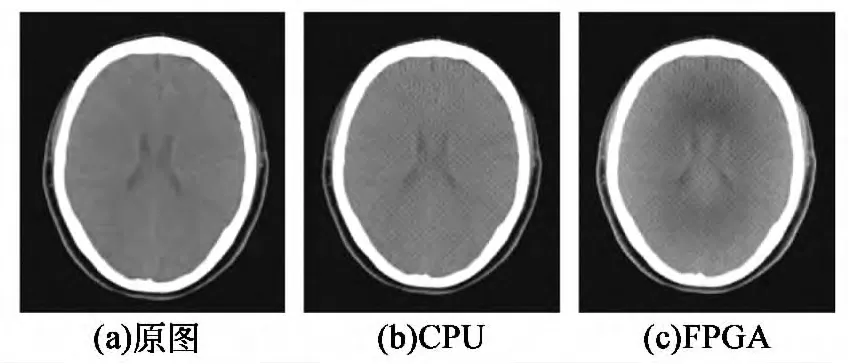
图8 脑部CT图像重建结果对比Fig.8 Reconstruction comparison of brain CT image

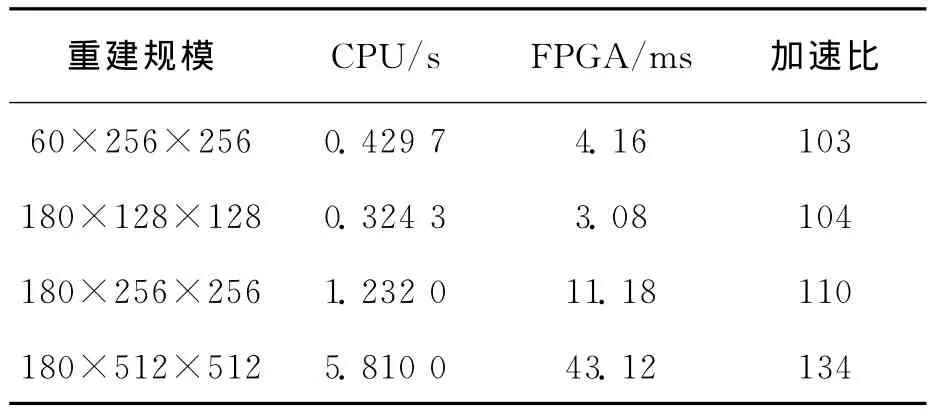
表1 重建速度对比Tab.1 Comparison of reconstruction speed

通过与基于CPU的图像重建速度对比，可以看出，基于FPGA的图像重建技术可达到100倍以上的加速比，且重建规模越大，加速效果越显著。

6 结 论

利用FPGA实现了图像重建FBP算法的加速，完成了算法模块的设计。利用查找表、IP核、逻辑运算替代乘除运算等优化手段，节省硬件资源的占用；采用双组缓存乒乓循环机制，实现反投影的无等待流水线，达到一个时钟更新一个重建点的速度。由于FPGA运算采用定点计算，计算结果会有一定偏差，文中采用了分级定点化的方法，有效平衡了精度与速度的矛盾。通过仿真验证，在重建图像精度损失较小的同时，得到了100倍以上的加速比。目前，影响加速效果的主要因素是FPGA硬件资源利用率和数据传输效率，随着FPGA技术的不断发展，可以实现更好的加速效果。

［1］ 邓建青，刘晶红，刘铁军.基于 DSP系统的查分辨率图像重建技术研究［J］.液晶与显示，2012，27（1）：114－120.Deng J Q，Liu J H，Liu T J.Super－resolution image reconstruction technology based on DSP system ［J］.Chinese Journal of Liquid Crystal andDisplay，2012，27（1）：114－120.（in Chinese）

［2］ Yan G，Tian J，Zhu S P，et al.Fast cone－beam CT image reconstruction using GPU hardware［J］.Journal of XRay Science and Technology，2008（16）：225－234.

［3］ 邹永宁，谭辉，黄亮.CT图像重建加速的几种方法［J］.计算机系统应用，2009（4）：167－170.Zou Y N，Tan H，Huang L.Research progress on CT image reconstruction acceleration ［J］.Computer Systems ＆Applications，2009（4）：167－170.（in Chinese）

［4］ 曾更生.医学图像重建［M］.北京：高等教育出版社，2010：21－30.Zeng G S.Medical Image Reconstruction：A Conceptual Tutorial ［M］.Beijing：Higher Education Press，2010：21－30.（in Chinese）

［5］ Coric S，Lesser M，Miller E，et al.Parallel－beam backprojection：An FPGA implementation optimized for medical imaging［C］／／Proc of the Tenth Int.Symposium on FPGA，2002（2）：217－226.

［6］ Aggarwal P，Mehra R.High speed CT image reconstruction using FPGA ［J］.International Journal of Computer Applications，2011，22（4）：7－10.

［7］ 邓靖飞，李建新，李磊，等.基于FPGA的CT重建加速技术综述［J］.CT理论与研究，2010，19（2）：25－33.Deng J F，Li J X，Li L，et al.Review of accelerated CT reconstruction based on FPGA ［J］.CT Theory and applications，2010，19（2）：25－33.（in Chinese）

［8］ 熊文彬，蒋泉，曲建军，等.基于FPGA实现的视频显示系统［J］.液晶与显示，2011，26（1）：92－95.Xiong W B，Jiang Q，Qu J J，et al.Video display system based on FPGA ［J］.Chinese Journal of Liquid Crystal and display，2011，26（1）：92－95.（in Chinese）

［9］ 曾政菻，刘学满.基于FPGA图形字符加速的液晶显示模块［J］.液晶与显示，2012，27（3）：352－358.Zeng Z L，Liu X M.LCD module based on FPGA accelerating graphics and characters processing［J］.Chinese Journal of Liquid Crystal and display，2012，27（3）：352－358.（in Chinese）

［10］ 孙红进.FPGA实现的视频图像缩放显示［J］.液晶与显示，2010，25（1）：130－133.Sun H J.FPGA realization of video image zooming display ［J］.Chinese Journal of Liquid Crystal and Display，2010，25（1）：130－133.（in Chinese）