基于四元数的彩色图像边缘检测研究
黄 鑫
(武警广东总队司令部,广东 广州 510660)
1 引 言
人们感知自然界中的色彩是一种感知现象,即可见光中任意波长的光都对应一种被感知的色彩,而不是光线本身的物理特征。典型的彩色图像的处理方法有两种,一种是针对彩色图像中各颜色分量进行分别处理,然后再进行合成;另一种方法是对彩色图像的像素进行处理,其中边缘检测是最为经典的方法。图像的边缘通常是图像的灰度或者颜色发生剧烈变化的地方,而这些变化往往是由物体的形状结构、外部的环境光照和物体的表面对光线反射造成的。图像的边缘能直接反应物体的轮廓和拓扑结构信息。
一般而言,考察每个像素在某个邻域内的亮度差信息时传统的边缘提取算法的实现依据,然而亮度差信息往往忽视了彩色图像的彩色信息。在现实生活中,人眼在观察物体或图像的感受则是颜色和亮度同时刺激视网膜上的神经元,其中颜色往往使人的感受更加强烈。因此,利用传统的边缘检测方法损失了大量的颜色信息,显然会造成检测不准确的问题。事实上,颜色的跳变通常更能反映图像的边缘信息。
彩色图像的边缘检测一般可采用如下3种方法实现:(1)首先将彩色图像转换为灰度图像,利用经典的灰度图像边缘检测方法予以实现边缘检测;(2)对彩色图像中像素的彩色分量分别实施灰度图像的边缘检测,最后在合成出最终的边缘检测结果;(3)利用矢量处理方法,即将彩色图像用一种矢量的方法予以整体处理,如色彩差分、矢量点乘等等[1-3]。
1987年Kass等人首次提出了主动轮廓模型(active contour model),又称snake模型。Snake模型通过定义一个与轮廓有关的能量函数,来表征轮廓的形状变化和行为变化使能量函数值趋向于变小的过程。当该能量函数达到最小值时,轮廓形状才定型、轮廓变化才停止。构造能量函数一般将图像特征、目标特征、边缘特征、文理特征全面考察,再使snake轮廓收敛于图像中的目标上。
传统的snake检测方法主要存在问题包括,初始位置敏感、检测效果依赖于能量函数模型的优劣等等。另外,这种检测也多见于灰度图像检测,在检测过程中存在信息和能力的损失。本文就彩色图像的边缘检测进行讨论,首先依据彩色图像的四元数表示,从而避免信息和能力的损失,然后利用snake模型实现彩色图像的边缘检测。
2 彩色图像的四元数表示
前文指出,传统的灰度图像边缘检测方法在进行彩色图像边缘检测时经常会失效,其原因在于常规边缘检测方法丢失了彩色图像的彩色信息或不能正确表达彩色信息。致使在进行边缘检测过程中可依赖的信息残缺不全,最终获得的检测结果与预想差距十分遥远。为此,在进行才彩色边缘检测时,首先需要解决的问题是对图像色彩信息的有效表达上。
目前,利用四元数描述彩色图像已经广泛被学术界认同,该方法利用矢量的思想对彩色图像的颜色信息能够全面表示,在最终的处理结果上也获得了良好的效果。四元数最早是由Hamilton在1853年提出的,其形式为:q=a+ib+jc+kd,其中a,b,c,d∈R;i,j,k满足关系i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j,则q为四元数,而称a为四元数q的实部,称ib+jc+kd为四元数q的虚部。
当实部为零时,称四元数为纯四元数。利用RGB模式表征的彩色图像的四元数表示可以用下式表达:
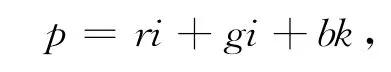
其中:r、g、b分别表示红、绿、蓝3种颜色分量的亮度值,即利用矢量的方法将一幅彩色图像中所有信息都全面表示出来了。从而使得在进行边缘检测时,可依据的信息变得非常全面[4-6]。
3 Snake模型原理
在Snake模型即活动轮廓模型,是一条能量参数曲线。轮廓跟踪的最小能量函数是外力和内力的加权和来表征的,所谓内力是通过Snake权限的形状计算得到;外力是从图像中获得或从更高级的图像处理中得到。参数化的Snake曲线被定义为V(s)=[x(s),y(s)],这里x(s)和y(s)是轮廓的坐标值,其中弧s∈[0,1],其最小化能量函数可以定义为
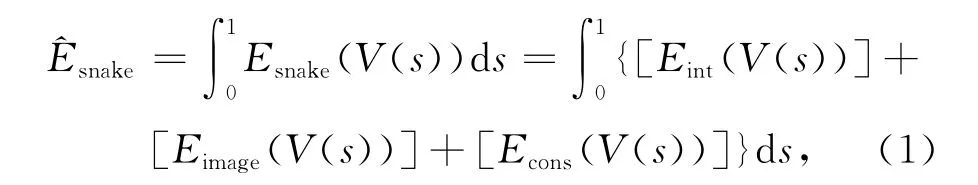
其中:Snake曲线因为弯曲产生的内部能力可以表示为

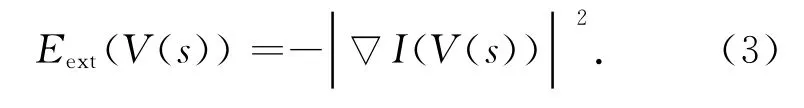
于是通过一阶导数求取最小化能量^Esnake的曲线V(s)必须满足:
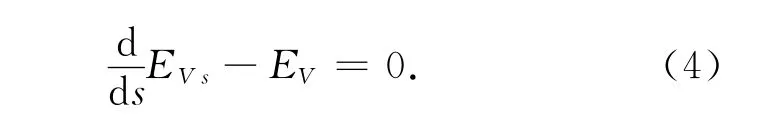
联立式(2)和式(4)可以简化式(3)得:

曲线的总能量可以用轮廓的弹性势能、轮廓的弯曲势能和图像有关的外部能量三项累加获得。其中外部能量是活动轮廓模型的关键,即描述了用何种数学表达来描述所要分割的物理边缘。Snake模型是把图像中感兴趣的物体轮廓看作一条连续的、封闭的或开放的链条结构,并设计了一类能量函数,通过求取能量最小值,来获得最优轮廓[7-8]。
Snake模型在进行图像边缘检测时具有很好的性能,但也有其局限性,主要表现在活动轮廓模型常导致能量函数收敛于局部最小;并且难于收敛到边界的凹陷位置。尤其针对彩色图像,其边缘信息较丰富,存在许多不规则边界凹陷部分。为此,要获得好的彩色图像边缘检测效果,必须在原有的Snake模型上进行改进。本文考虑到彩色图像时利用四元数进行描述的,而双四元数通过傅里叶变换可以获得图像局部的显著性特征,利用这一特性来获取图像的粗轮廓,然后采用3×3模板构造活动轮廓的能量函数,从8个方向上求取梯度实现能量收敛,从而实现边缘逼近[6-9]。
4 双四元数和Snake边缘检测算法
4.1 双四元数傅里叶变换计算轮廓
众所周知,图像的频率是表征图像中色彩变化剧烈程度的指标,是色彩/能量在平面空间上的梯度。如:广阔的蓝天或草地在图像中是一片色彩变化缓慢的区域,对应的频率值很低;而对于图像中天际线的位置其颜色属性变换相对剧烈,即图像中色彩变化剧烈的区域往往是图像的边缘区域,所对应的频率值也相对较高。利用傅立叶变换可以很好地对图像的边缘和频率进行表征和变换计算。设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。
为此,用双四元数表示彩色图像,通过傅里叶变换获得该图像的谱,边缘区域表征谱值较高的色彩变化剧烈的区域,从而可以获得彩色图像的粗边缘轮廓。
设二维图像表示为f(x,y),其双四元数的表示形式如下:
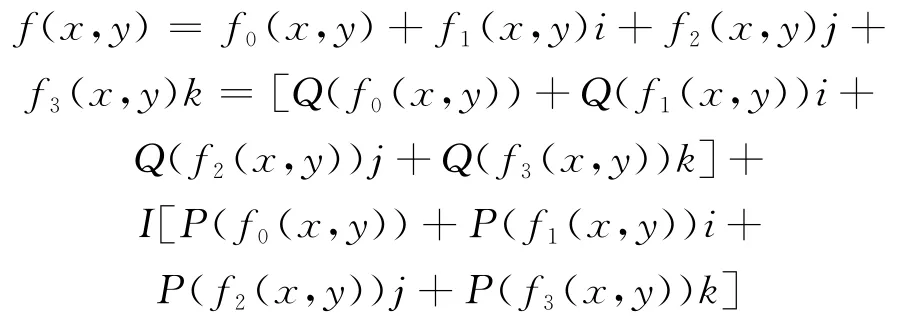
通过线性变换,可将基i,j,k变换为复正交基μ,v,ξ,其中 μ⊥v,v⊥ξ,μ⊥ξ,μv=ξ,μvξ=-1,μ,v,ξ都是纯双四元数。在新的复正交基系统中,f(x,y)可描述为:
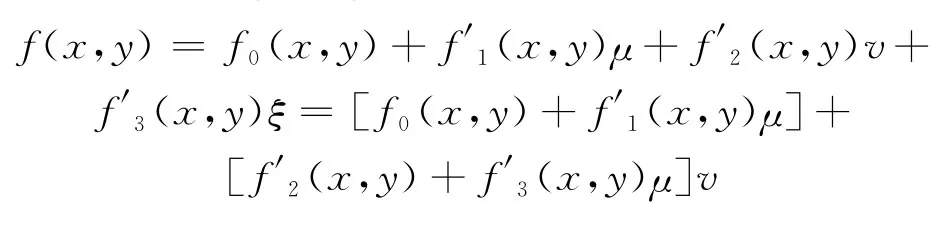
由于彩色图像的f0(x,y)=0,对上式进行快速傅里叶变换可表示为
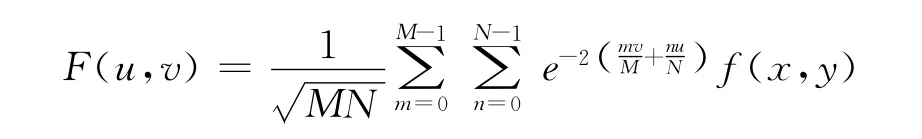
这里显然F(u,v)也是一个四元数,通过对其频谱函数进行分析,即可得到彩色图像的粗轮廓[8-11]。
4.2 利用Snake模型获取最终边缘
前面给出了双四元数傅里叶变换的基本方法,即从频域的角度在保证彩色图像颜色信息的前提下的彩色图像粗轮廓,接下来需要利用活动轮廓模型进一步得到最终的彩色图像边缘检测。由于Snake模型中定义的能量函数在迭代中可能出现局部极值,并且迭代结果好坏与初始轮廓直接相关,为进一步完成Snake迭代,将在梯度向量场的8个方向上进行,从而改进原有模型缺陷。
具体算法可以表述如下:
(1)读入待处理的彩色图像;
(2)对待处理的彩色图像进行四元数傅里叶变换后得到的结果作为Snake算法模型的初始Edge(V(s));
(3)在梯度矢量场中,使用8个方向上分量进行迭代,迭代结果作为Snake算法模型中的外力表达;
(4)在当前邻域内找到能量函数的最小像素点;对能量函数完成迭代直到收敛。
4.3 仿真实验分析
为了对算法进行检验,本文给出了3组实验用来验证算法的可行性和检测效果。第一组实验用一幅彩色色带图像,分别对其颜色分量进行检测,通过对比灰度边缘和基于双四元数Snake算法的边缘检测的可行性;第二组采用经典的Lena图像进行彩色边缘检测和Sobel边缘检测,主要检验算法的边缘检测效果;第三组实验利用本文给出算法与高斯
(1)彩色彩带图像的检测实验

图1 实验(1)图例Fig.1 Experiment(1)legend
在实验(1)中图a是人工合成的彩色渐变图,图中从红色到红色实现了颜色的渐变,主要用于测试四元数snake彩色边缘检测算法的可行性。图中的b、c、d分别是单色颜色分量的检测结果。从单色图像可以看出,在颜色发生改变的位置,刚好是图像的边缘所在位置,这也正是论文采用四元数来表征颜色分量,利用矢量计算方式保留颜色分量用于边缘检测的思想的正确性。
图e是彩色渐变图的灰度图像,f、g分别是实现snake边缘检测的中间和最后过程。从图f可以看出,彩色渐变图最终的检测结果,能够将颜色发生变化的位置的边缘显示出来。
(2)Lena图像的边缘检测实验
在第二组实验中,采用经典的Lena图像进行实验,如图2所示。在这组实验中用了两种方法,其一是用经典的Sobel边缘检测算法,首先将彩色图像灰度化,如图3所示。在对该图像进行Sobel边缘检测,得到如图4所示。经典的Sobel算法能够较好地获得图像的边缘,但由于Sobel算子在处理边缘是丢失了彩色分量信息,使得在边缘,如帽子饰品、头发等部位较为粗糙。其二,采用本文给出的算法,首先利用双四元数将彩色图像进行编码处理,如图5所示;然后在对该图像进行snake处理,即在梯度矢量场中,使用8个方向上分量进行迭代,当能量函数收敛后,得到图6的检测结果。

图2 原始图像LenaFig.2 Original image Lena

图3 Lena的灰度图像Fig.3 Gray image of Lena

图4 Sobel算子的Lena边缘检测Fig.4 Sobel operator edge detection of Lena

图5 基于双四元数编码处理Fig.5 Encoding process based on dual quaternion

图6 Snake算子边缘检测灰度图像Fig.6 Snake grayscale image edge detection operator
从上述实验可以看出,算法能够较快速地完成彩色图像的边缘检测,并能获得较好的检测效果。通过对彩色边缘结果进行灰色处理后同Sobel算法的结果比较,可以发现彩色边缘检测完整,保留了色彩信息,在处理颜色变化位置的细节上具有明显的优势,图像的边缘较传统的Sobel算法的边缘检测要清晰很多。
(3)算法检测效果和效率
在这组实验中,选取图7作为检测图像。分别对该图进行Soble、本文算法的彩色边缘检测和第三方图像处理软件CS4的边缘检测,并统计处理时间,然后分析处理效果和执行效率。

图7 待处理图像Fig.7 Image to be processed

图8 Sobel算子检测效果Fig.8 Detection effect of Sobel operator

图9 本文算法检测结果Fig.9 This algorithm test results
从上面的处理结果看,本文算法在处理颜色变化部位的边缘能力更为突出,CS4处理软件在颜色变化区域边缘获得的比较平滑。表1给出3种方式的时间统计,所用的机器是I5 2400,4G内存,GT640的显卡,图像大小440×658像素。

图10 CS4边缘检测结果Fig.10 Edge detection results CS4

表1 边缘检测算法统计时间对照表Tab.1 Edge detection algorithm statistical time table
上面的统计中除CS4统计的不够精准外,其他两个都是在程序中对系统时钟累计的结果。从执行效率看,本文给出的双四元Snake方法略慢,原因在于双四元傅里叶变换以及进行了8个方向的梯度分量迭代,然后在进行动态轮廓处理,从而导致耗费时间较多。但前面已经指出,算法处理效果略好于其他两外两种方法。因此,在下一步研究中,需要进一步提高算法的执行效率。
5 结 论
通过理论分析指出,传统的灰色图像边缘检测存在信息损失的问题,故此,对彩色图像进行四元数描述。同时,根据双四元数傅里叶变换可以获得彩色图像显著性特征的这一特性,利用其获得彩色图像的初轮廓提取,以此作为Snake算法的初始Edge(V(s)),然后利用经典的Snake算法进行能量函数迭代,通过实验取得了比较好的检测结果。
[1] Pei S C,Cheng C M.Color image processing by using binary quaternion moment preserving thresholding technique[J].IEEE Transactions on Imaging Processing,1999,8(5):614-628.
[2] 陶李,王珏,邹永宁,等.改进的Zernike矩工业CT 图像边缘检测[J].中国光学,2012,5(1):48-56.Tao L,Wang J,Zou Y N,et al.Improved Zernike moment method for industrial CT image edge detection[J].Chinese Optics,2012,5(1):48-56.(in Chinese)
[3] Cai C,Mitra S K.A normalized color difference edge detector based on qua tern ion representation[C]//Proceedings of IEEE International Conference on Image Processing Vancouver,Canada,2000:816-819.
[4] Ell T A,Sang wine S J.Hyper complex Fourier transforms of color images[J].IEEE Transactions on Image Processing,2007,16(1):22-35.
[5] Koschan A,Abidi M.Detection and classification of edges in color images[J].IEEE Signal Processing Magazine,2005,22(l):64-73.
[6] Naik S K,Murthy C A.Standardization of edge magnitude in color images[J].IEEE Trans.Image Processing,2006,15(9):2588-2595.
[7] 康晓晶,吴谨.基于高斯背景建模的目标检测技术[J].液晶与显示,2010,25(3):454-459.Kang X J,Wu J.Object detecting technology based on gauss background modeling[J].Chinese Journal of Liquid Crystals and Displays,2010,25(3):454-459.(in Chinese)
[8] 同武勤,凌永顺,黄超超,等.数学形态学和小波变换的红外图像处理方法[J].光学精密工程,2007,15(1):139-144.Tong W Q,Ling Y S,Huang C C,et al.Processing method of IR image based on mathematical morphology and wavelet transform [J].Optics and Precision Engineering,2007,15(1):139-144.(in Chinese)
[9] Christopoulos C,Askelof J,Larsson M.Efficient methods for encoding regions of interest in the upcoming JPEG 2000still image coding standard[J].IEEE Signal Processing Letters,2000,7(9):247-249.
[10] 赵才荣,刘金娥,丁铁夫.基于LED图文屏的多灰度图像实现方法[J].液晶与显示,2006,21(1):82-86.Zhao C R,Liu J E,Ding T F.Chinese method of multi-grey image realization based on chart-article led screen[J].Journal of Liquid Crystals and Displays,2006,21(1):82-86.(in Chinese)
[11] Chan T F,Sandberg B Y,Vee L A.Active conturs without edges for vector valued images[J].Journal of Visual Communication and Image Representation,2000,11(2):130-141.

