激光强度值改正模型与点云分类精度
谭 凯,程效军
(同济大学 测绘与地理信息学院,上海 200092)
地面三维激光扫描(terrestrial laser scanning,TLS)在获取探测对象表面高密度的散乱点云的三维坐标信息的同时,也可获取点云的色彩信息R、G、B和激光强度值I(laser intensity).如何根据目标特有的属性将这些散乱无组织的点云进行分类以建立其拓扑关系,是地面三维激光扫描数据处理中首先要解决的问题.目前点云分类主要的方法是借助点云的几何信息,计算量大,效率低下,精度也不高[1].而激光强度是目标对发射激光光束的后向散射回波的光功率[2],它作为反映目标特性的重要特征值,包含目标表面特征信息,利用其可实现点云直接的、高效的和精确的分类[1-3].本文通过分析地面三维激光扫描激光强度值的影响因素,从激光雷达方程及扫描仪内部工作原理出发,分别建立线性、对数、三次多项式模型拟合激光强度值与各种影响因素之间的关系,在此基础上提出了相应的物理改正模型对各种因素进行改正,利用改正后的强度值进行点云分类,同时对三种模型改正效果、分类精度、运算效率等进行了比较分析.
1 激光强度值的物理改正模型
激光强度是目标对发射激光光束的后向散射回波的光功率,激光回波信号被接收机接收后在接收机内部转换和放大,最终转换成激光强度值.由于受到系统变量和目标变量的影响,强度值存在较大偏差.强度值影响因素中的系统变量主要包括激光测距值、激光入射角、大气衰减、信号处理等;目标变量则主要包括目标反射率、目标粗糙度、目标尺寸、目标倾斜度等[1-6].强度值改正目的就是要去除系统变量的影响,使强度值中仅包含目标变量的信息,使其能直接反应目标属性信息.因此,首先必须建立激光强度值与各种系统变量之间的函数关系,在此基础上才能分析各种系统变量的影响并对其进行相应的改正.
激光雷达方程可以看成发射一定功率激光后的激光大气传输、目标特性、光学系统传输特性和接收机4项因子的乘积形式[7],因此可从激光雷达方程出发,建立强度值与系统变量之间的模型关系.对于扩展的朗伯散射体,激光雷达方程可简化为[2]
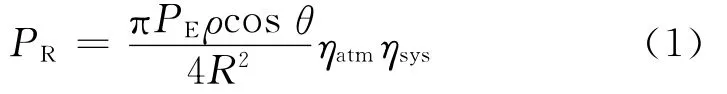
式中:PR为接收激光功率;PE为发射激光功率;R为激光测距值;ηatm为单程大气传输系数;ηsys为激光雷达的光学系统传输系数;ρ为扩展目标的平均反射系数;θ为激光入射角.
由式(1)可知,激光雷达方程将接收功率PR与系统变量(测距值R、入射角θ)联系起来,因此寻求激光强度值I与系统变量的关系转换为寻求激光强度值与接收功率PR之间的关系.在接收机内部[1],回波信号的功率(或能量)PR或者回波信号的峰值振幅被转换为电压,再经雪崩光电二极管(APD)放大,通过未知的专有函数进行数字化,最终转换为一个标定的整数(digital number,DN),这个整数即是最终获得的激光强度值I.因此激光强度值与在特定的时间间隔内光子撞击探测器的次数(即接收功率PR)成正相关(I∝PR)[1],即激光强度值I与接收功率之间存在关系I=f(PR),f为增函数.由于各扫描仪生产厂家对函数f的具体形式保密,所以并不能直接获得I与PR之间的关系,只能通过数据拟合来分析f的具体形式,本文通过线性模型、对数模型及三次多项式模型三种方法进行拟合.
1.1 线性模型
线性模型假定激光强度值与接收功率之间存在线性关系,即:
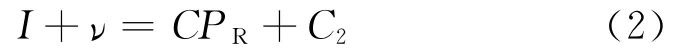
式中:I为实测激光强度值;ν为观测误差;C、C2为模型系数,只与目标属性信息有关.
对于地面三维激光扫描,由于测距较短,大气传输系数ηatm、光学系统传输系数ηsys可以忽略不计,同时发射功率PE稳定,而强度值改正的目的就是要对系统变量(入射角、测距值)进行改正,使改正后的强度值中仅包含目标属性信息(反射率ρ),因此由式(1)可知,可用cosθ/R2替代PR,则式(2)可写为

式中:C1为模型系数,只与目标属性信息有关.
由式(3)可知,由于激光入射角及激光测距值的影响,同一目标测得的激光强度值可能不同,因此必须去除激光测距值及激光入射角的影响,将其改正至相同的距离以及相同的入射角下,才能使强度值中仅包含目标属性信息.设参考入射角为θs,参考距离为Rs,实际入射角为θ,实际测距值为R,据此可建立激光强度值的线性改正模型:

式中:I为实际测得的激光强度值,其受到激光入射角、激光测距值以及目标属性信息的影响;Is为改正后的激光强度值,其只包含目标属性信息.
1.2 对数模型
对数模型假定接收机将接收功率对数转换后再转换为激光强度值,同线性模型,用cosθ/R2替代PR,即:
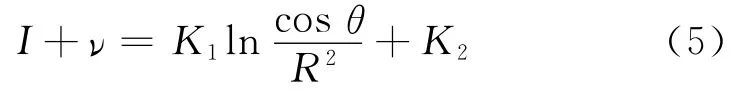
式中,K1、K2为模型系数.则激光强度值的对数改正模型为
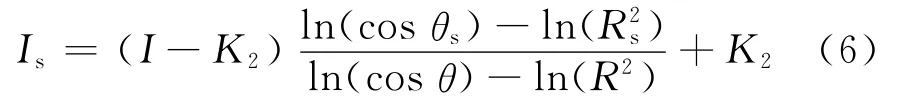
1.3 三次多项式模型
同线性模型与对数模型,三次多项式模型为
式中,λ1、λ2、λ3、λ4为模型系数.相应的三次多项式改正模型为
由式(1)~(8)可知,物理改正模型是从激光雷达方程及激光强度值与激光后向散射功率(即接收功率)的关系出发,建立强度值与入射角及测距值之间的函数关系,在此基础上对系统变量进行改正,将激光强度值改正至相同的入射角及相同的测距值条件下,使强度值可直接反映目标属性信息.
2 三种改正方法实例分析及对比
本文实验采用Leica三维激光扫描仪扫描某一用石灰粉刷的白色墙体(可看成表面性质均匀的扩展朗伯散射体),扫描获得点云的三维坐标(X,Y,Z)以及强度值I,再通过区域拟合法求得每一点的单位法矢(n1,n2,n3),运用(9)式可求得激光测距值R和激光入射角θ.
2.1 三种改正方法拟合效果比较分析
由式(3)、(5)、(7)可建立以下间接平差模型求取各模型的模型系数:
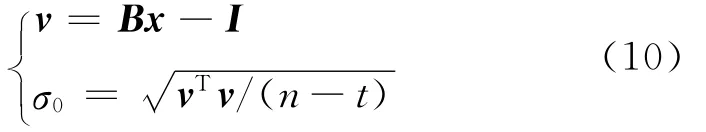
其中:B为系数阵;x为待求模型系数矩阵;n为点云数量;t为模型系数个数;σ0为拟合中误差.
选取实验数据中的某站数据共8 832个点云,采用三种方法分别进行拟合,求得各个模型的参数.同时求得线性模型、对数模型、三次多项式模型的拟合中误差分别为79.20,66.73,21.75,由此可知三次多项式模型拟合效果最好,对数模型次之,线性模型最差.
如图1所示,以cosθ/R2(单位:m-2)为横轴,I为纵轴,作出原始激光强度值I(量纲一)与cosθ/R2的散点图,并将表1中所求得的三种模型与其进行对比(分别如图1b、1c、1d所示),由图可知,三次多项式模型图像与原始图像最为接近,拟合效果最好,对数模型次之,线性模型最差.
2.2 三种模型强度值改正
根据式(4)、(6)、(8)分别求取三种模型改正后的激光强度值,以点号为横坐标,激光强度值I(量纲一)为纵坐标,原始强度值及三种模型改正后的强度值分别如图2所示.
分析图2可得:对于实验中表面性质均匀的白色墙体,改正前,各点激光强度值受到系统变量的影响,相差较大,标准差为512;改正后,去除了系统变量的影响,强度值较为接近.除少数异常点外,对数改正模型与三次多项式改正模型改正后的激光强度值组成的散点图接近一条直线,改正效果较好;而线性改正模型改正后的激光强度值组成的散点图整体趋近一条直线,存在一定偏差.为了定量地对三种模型的改正效果进行比较,分别求取其改正后的强度值的标准差:三次多项式模型改正后强度值标准差为27,强度值之间较为接近,改正效果最好;数模型改正后强度值标准差为58,改正效果次之;而线性模型改正后的强度值标准差为175,改正效果最差.
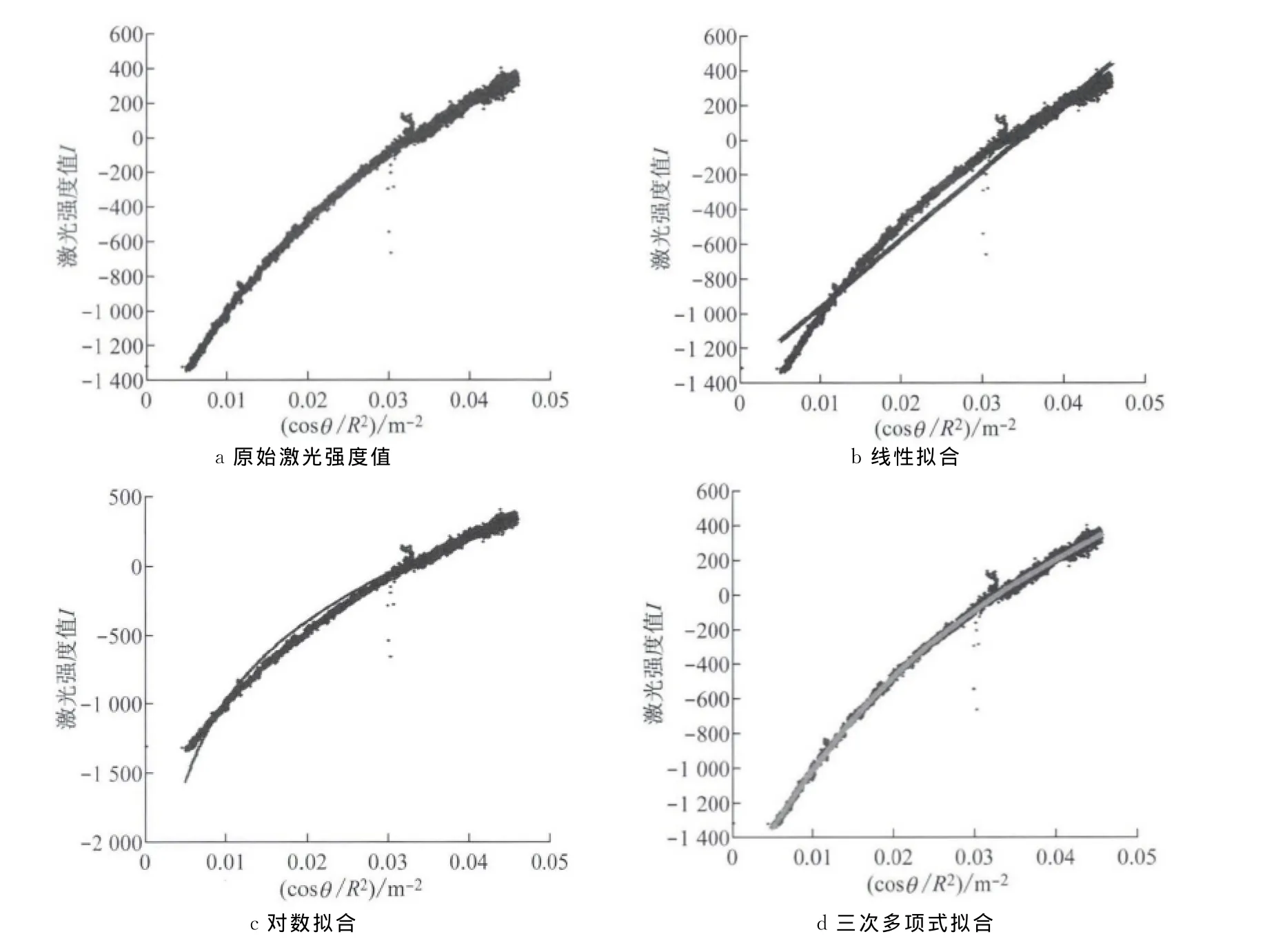
图1 三种改正方法拟合效果比较Fig.1 Comparison of the fitting effect of the three models
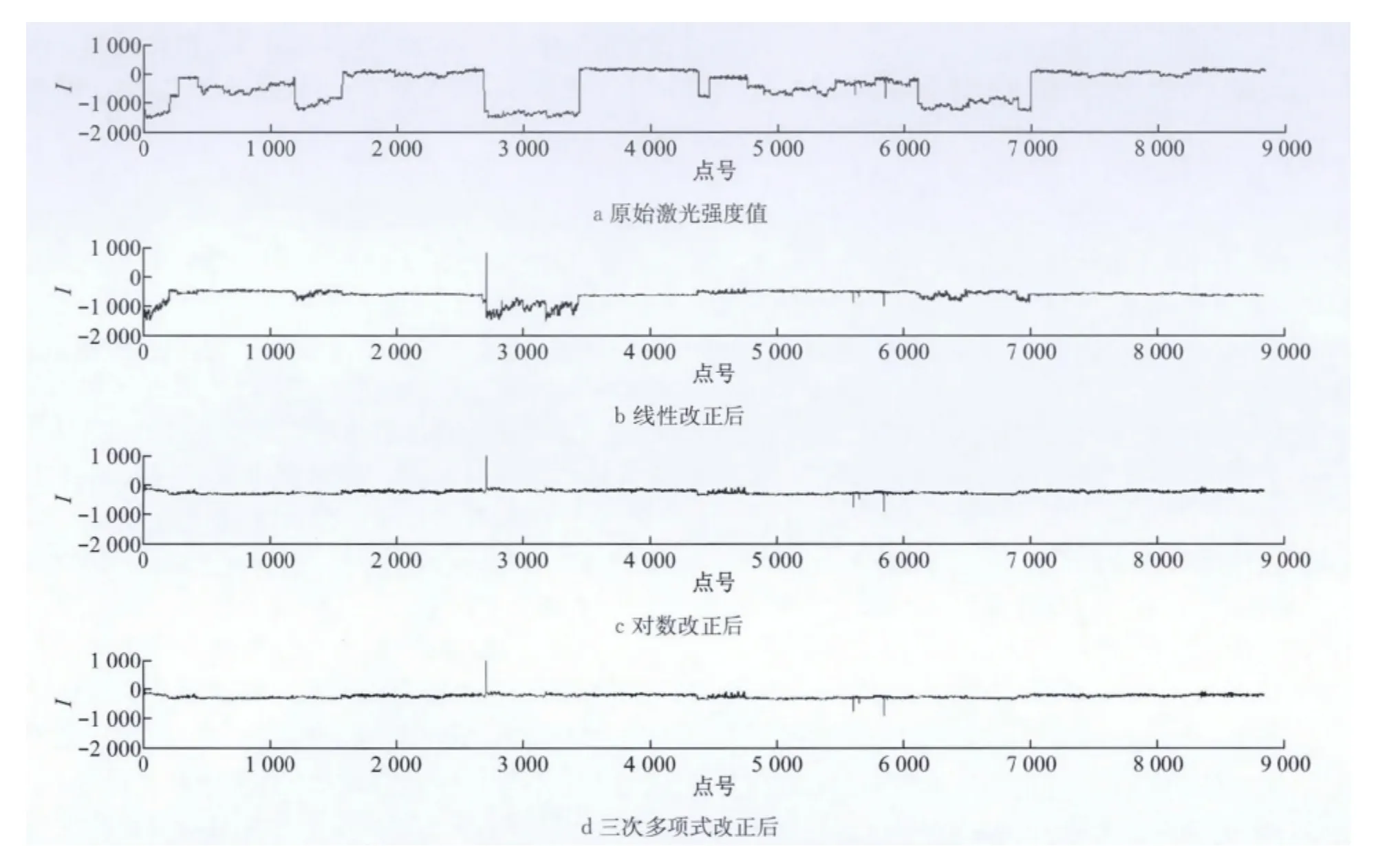
图2 原始激光强度值及三种模型改正后的激光强度值Fig.2 The original laser intensity values and the values corrected by three models
3 基于强度值的点云分类及实例分析
改正后的强度值,去除了系统变量的影响,只包含目标属性信息,利用其可实现点云分类.利用上述实验中原始及改正后的强度值,如图3所示,从强度值的最小值开始,以250单位为间隔对点云进行分类,不同区间代表不同的类别,用不同颜色表示,其中正确分类点云已标出.图3a表示原始激光强度值分类的结果,利用原始强度值将点云分成了7类,由图可知,相近区域由于激光测距值及激光入射角接近,测得的强度值也较为接近,反之亦然.图3b、3c、3d分别表示线性模型、对数模型、三次多项式模型改正后激光强度值进行点云分类的效果,从图中可以看出,三次多项式模型的分类效果最好,对数模型次之,线性模型分类效果最差.
为了定量地对原始激光强度值及三种模型的分类效果进行比较,在Matlab中分别对其分类精度及运算效率进行了比较,见表1.从表中可知,对于实验中的8 832个点云,原始激光强度值用于点云分类的精度仅为9.84%,而线性模型、对数模型、三次多项式模型的分类精度分别为84.38%、97.54%、99.59%,分类精度大大提高.分类精度提高的同时,运算效率也依次降低,原始强度值、线性模型、对数模型、三次多项式模型的运算效率分别为94.95s、103.64s、104.27s、107.46s.

表1 激光强度值用于点云分类的精度与效率Tab.1 The accuracy and efficiency of point cloud classification by the laser intensity values
4 结语
本文从激光雷达方程出发,分别采用线性模型、对数模型以及三次多项式模型对强度值进行改正,并基于改正后的强度值进行点云分类.结果表明:三种模型都能很好地对强度值进行改正,改正后的强度值都能很好地提高分类精度,为强度值在地面三维激光扫描仪中的进一步应用提供了理论基础,同时也提出了一种崭新的点云分类的方法;线性模型分类精度最低,运算量小;三次多项式模型分类精度最高、运算量大;对数模型精度与运算量兼顾.物理模型改正是针对理想的朗伯散射体,未考虑误差的存在,但扫描中存在各种未知的系统误差和偶然误差,因此深入分析激光强度值的影响因素及各种误差,针对实际扫描数据,建立更加完善和精确的数值改正模型进行点云的自适应分类以及利用点云分类的结果进行建模与特征提取等是后续研究的重点.

图3 原始激光强度值及三种模型改正后激光强度值进行点云分类Fig.3 Point cloud classification of the original laser intensity values and the values corrected by three models
[1] Höfle B,Pfeifer N.Correction of laser scanning intensity data:Data and model-driven approaches[J].ISPRS Journal of Photogrammetry and Remote Sensing,2007,62(6):415.
[2] Pfeifer N,Dorninger P,Haring A,et al.Investigating terrestrial laser scanning intensity data:quality and functional relations[C]//Proceedings of the VIII Conference on Optical 3D Measurement Technology.Zurich:[s.n.],2007:328-337.
[3] Coren F,Sterzai P.Radiometric correction in laser scanning[J].International Journal of Remote Sensing,2006,27(15):3097.
[4] Cheng X J,Tan K,Lou Q Y.Relations of the laser intensity value,the laser ranging value and the laser incident angle[J].Applied Mechanics and Materials,2013,239:198.
[5] Kaasalainen S,Jaakkola A,Kaasalainen M,et al.Analysis of incidence angle and distance effects on terrestrial laser scanner intensity:search for correction methods[J].Remote Sensing,2011,3(10):2207.
[6] Vain A,Kaasalainenet S,HyyppäJ,et al.Calibration of laser scanning intensity data using brightness targets[J].Geodesy and Cartography,2009,35(3):77.
[7] 戴永江.激光雷达原理[M].北京:国防工业出版社,2002.
DAI Yongjiang.Laser radar principles[M].Beijing:National Defense Industry Press,2002.

