含多交易对手信用违约互换的信用风险模型
梁 进,李文毅
(同济大学 数学系,上海 200092)
从2009年底的迪拜债务危机到去年的欧洲债务危机,再到目前全球范围内的通胀危机,都显示世界经济还没有从美国次贷危机的阴霾中走出来.这些危机凸显场外衍生工具市场交易对手风险的重要性,特别是信用衍生工具.
大多数的场外衍生品交易都有交易对手的信用风险.在巴塞尔协议II中,交易对手信用风险(counterparty credit risk,CCR)被定义为:“一桩交易的对手方可能在交易现金流最后结算前发生违约;如果这桩交易或资产组合在违约时对本方有正的经济价值,那么对本方就会发生经济上的损失.”过去的十年中,场外交易飞速发展,但直到2008年次贷危机爆发才使其违约风险被广泛受到关注.这次金融危机造成了自1930年经济大萧条后全球范围内的一次巨大的经济衰退.而交易对手信用风险也在这次金融危机中扮演了重要的角色.
信用违约互换(credit default swap,CDS)可以显示市场中交易的“信用健康”.CDS的出现解决了信用风险的流动性问题,使得信用风险可以像市场风险一样进行交易,从而转移担保方风险,同时也降低了企业发行债券的难度和成本.但是基于分散风险的原则,在错位风险的情况下,对信用衍生产品进行风险度量与控制时有一个问题令风险规避方感兴趣:一份风险资产合约是否可由多名交易对手来承担风险?如果是,那么他们之间的违约正负相关性怎样影响风险?所以如何建立合理的数学模型来研究这样的风险就是本文的课题.
交易对手估值调整(counterparty valuation adjustment,CVA)被用来估算交易对手的信用风险.换句话说,CVA就是考虑和不考虑交易对手违约风险情况下对某合约估值的差额.Pykhtin等[1]和Alavian等[2]对交易对手信用风险以及CVA作了概括和综述.Brigo[3]在约化法的框架下考虑了交易对手信用风险,并对违约强度和无风险利率的相关性作了分析.他们还在文献[4]中用约化法对考虑交易对手违约风险的权益信用违约互换(contingent credit default swap,CCDS)进行了研究,同样也对违约强度和利率的相关性作了分析,其违约强度被扩展到跳扩散过程.Brigo等[5]将交易对手信用风险的研究从单边的扩展到了双边.Li在文献[6]考虑了带交易对手信用风险的CDS定价是将回收率假设为随机过程.魏嵬和姜礼尚[7]利用单因子模型对标准的单名CDS产品的CVA作了计算和分析.
本文将在模型[7]基础上考虑含多交易对手的单名CDS产品的CVA计算模型,通过分析考虑交易对手之间违约的相关性,分别用单因子CIR(Cox-Ingersoll-Ross)模型和单因子反CIR模型刻画正负相关性,并在约化方法的框架下得到CVA的计算模型,并在这个基础上作了一些数值结果的分析,同时将多交易对手的CDS与标准的CDS的CVA值进行做比较分析,进而得出一些有指导意义的结论.
1 建立模型
1.1 多交易对手单名CDS的现金流分析
现在考虑多交易对手的单名CDS合约的现金流,假设这张合约中有两个交易对手B1,B2,一个参考公司C,对应符号的上、下标i(i=1,2,3)做如下的假设:交易对手Bi→i(i=1,2),参考公司C→i=3.
在约化法框架下,违约可用强度模型来刻画.假设τi表示第i(i=1,2,3)公司的违约时间,定义违约指示过程,其中Hi是这三个违约过程生成的信息流.即,其中以及σ-域流,对所有t∈R+.ht包含了这份合约是否终止的所有信息.假设其中为市场上所有可知信息.假设τi是Gt-停时,即事件(τi≤t)(i=1,2,3)属 于σ-域 流Gt.所 以τi是 概 率 空 间 (Ω,Gt,{Gt}t≥0,P)上的随机时间,其中P是风险中性概率.
在标准CDS基础上考虑多交易对手,其他条件不变.如保费是定期支付,赔付在违约发生时,剩余保费将在下个支付日支付.合约到期日为T,参考贷款面值为1.保费支付日为t1<t2<…<tM=T,M为总期数,Δt为相邻保费支付日间隔,R1为参考公司的回收率.新的假定是:如果一个交易对手在参考公司违约之前违约,则该交易对手所担保的比例马上结算,而投资者与另一交易对手的合约继续.如果参考公司C在两个交易对手之前发生违约,CDS卖方B1,B2按相应比例a1,a2进行赔付,分别为:ai(1-R1),(i=1,2,a1+a2=1),则多交易对手的单名CDS合约的具体现金流如图1所示.图中,τ3为参考公司违约时刻,a1(1-R1)为交易对手B1的赔付,a2(1-R1)为交易对手B2的赔付.其中,R2为CDS卖方B1,B2发生违约时的回收率.
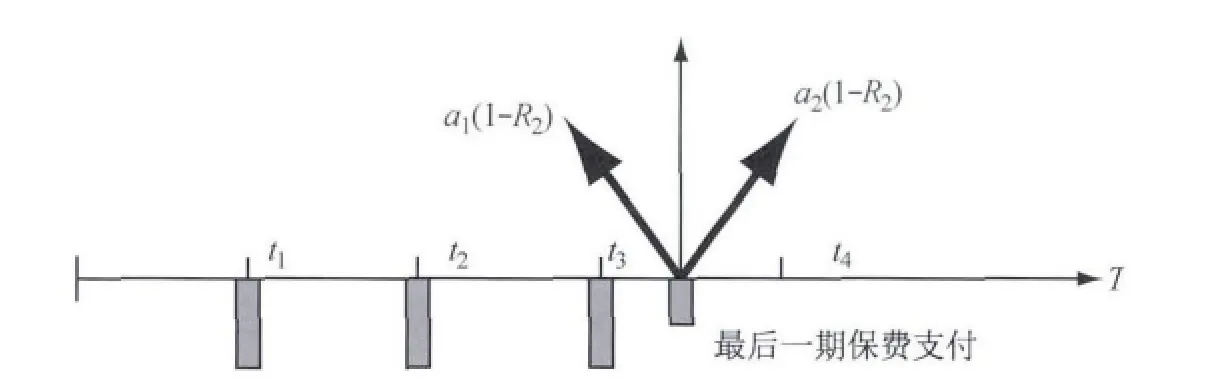
图1 多交易对手信用违约互换现金流图Fig.1 Cash flow of the multi-counterparties credit default swap products
1.2 含多交易对手单名CDS合约的CVA计算模型
假设r为无风险利率,U为考虑了CCR的含多交易对手的单名CDS的价值,V为不考虑CCR的含多交易对手的单名CDS的价值,λi表示第i(i=1,2,3)公司的违约强度.如果CDS卖方Bi(i=1,2)先于参考公司违约,买方的损失(或收益)为[8]ai(R2U+-U-).站在t时刻,不含CCR的多交易对手CDS合约的价值为:
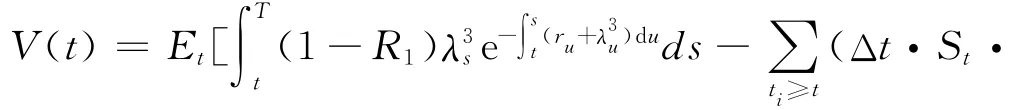

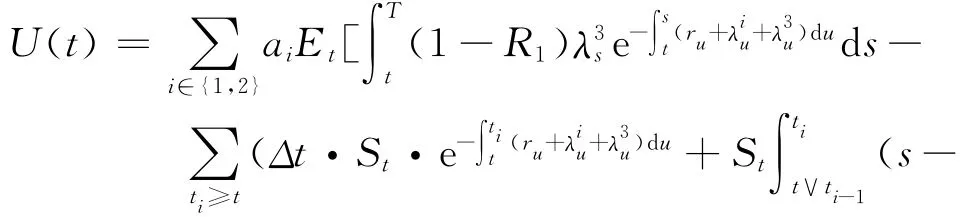
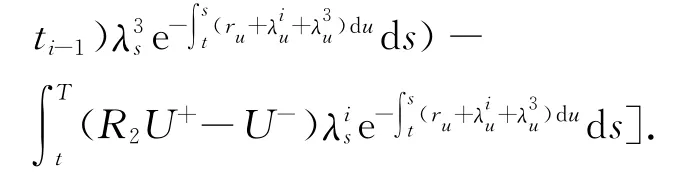
其中:U+=max{U,0},U-=min{U,0},r为无风险利率.
那么多交易对手CDS合约的CVA在t时刻的估值为
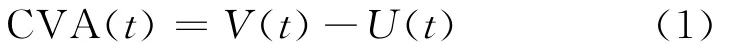
1.3 单因子CIR模型
(1)多交易对手与参考公司之间违约相关性为正相关情形
考虑利用单因子模型来建立参考公司违约与交易对手违约之间的相关性.在前言部分分析CDS的信用风险中,已经强调了利率作为宏观经济变量的重要性.利率不仅关系到整个国家的经济运行,同样对每个投资者也是十分重要的投资因素.所以利用rt表示公共因子即系统性风险因子,而βit(i=1,2,3)则表示第i公司违约的特有因子即非系统性风险因子,得到下面的单因子模型:
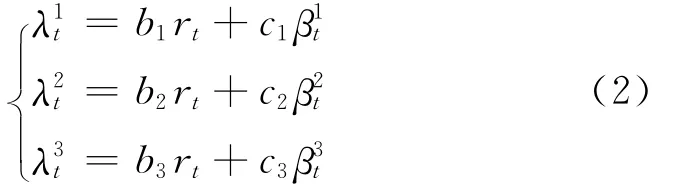
式中,bi和ci都是非负常数,并且是相互独立的随机过程.
假设瞬时无风险利率rt和βit(i=1,2,3)都由CIR过程驱动,即
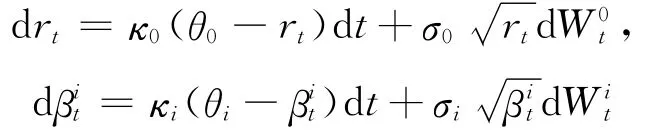
其中κi、θi和σi是正的常数,并且满足Feller条件是相互独立的标准布朗运动(i=0,1,2,3).
(2)多交易对手与参考公司之间违约相关性为负相关情形
现在考虑参考公司与交易对手之间的违约是负相关的,即宏观利率因素对两者的影响是反向的.为保证所有的(i=1,2,3)均为正,假设[8]:
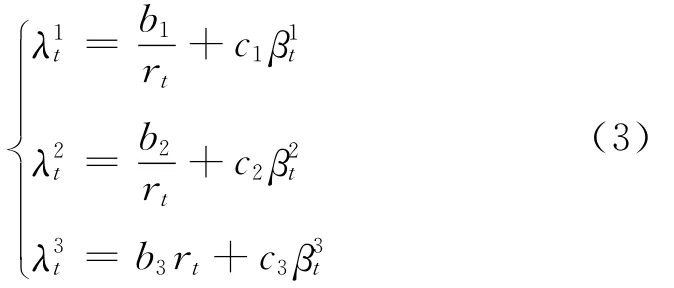
其中bi和ci均为非负常数,同样假设是相互独立的随机过程.这样之间的违约相关性为正相关,而分别与之间的违约相关性为负相关的.
(3)一个交易对手与参考公司之间的违约相关性为正相关而另一个交易对手与参考公司之间的违约相关性为负相关情形
现在考虑参考公司与交易对手之间的违约有正相关的,也有负相关的情形,即宏观利率因素对一个交易对手的影响为正,另一个为负,此时假定:
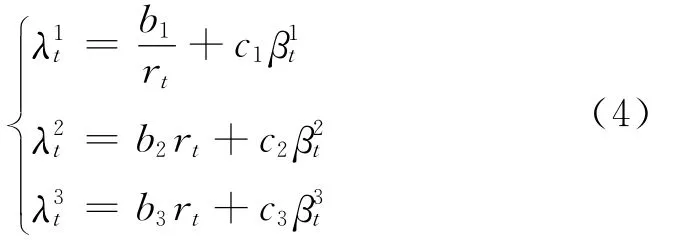
其中bi和ci均为非负常数,同样假设是相互独立的随机过程.这样之间的违约相关性为正相关之间的违约相关性是负相关的.
模型(3)中第①式含有1/rt项,其为CIR过程的倒数,满足反 CIR过程[9](inverse CIR process,ICIR).
2 模型求解
本文的模型求解分为线性的和非线性的,首先解决线性问题的解.
2.1 模型的线性问题求解
2.1.1 单因子CIR模型的情形
建立了单因子CIR模型后,便可以对CVA值式(1)进行求解了.观察式(1),求解关键在于求类似于的条件期望.将模型(2)代入这两个期望表达式可化为求解 如 下 两 个 基 本 类 型 的 期 望:和.对于形式(I)的期望,可以通过求解下面偏微分方程的 Cauchy问题其中k为常数:
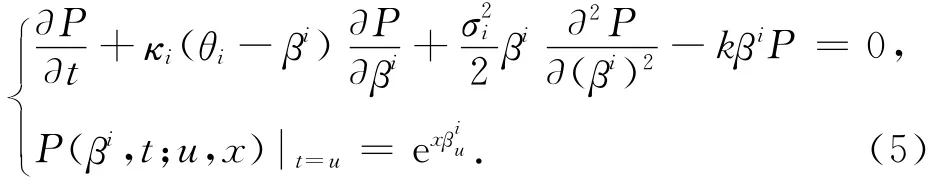
偏微分方程(5)有仿射形结构解[10].即存在函数A(t,x)和B(t,x),使得

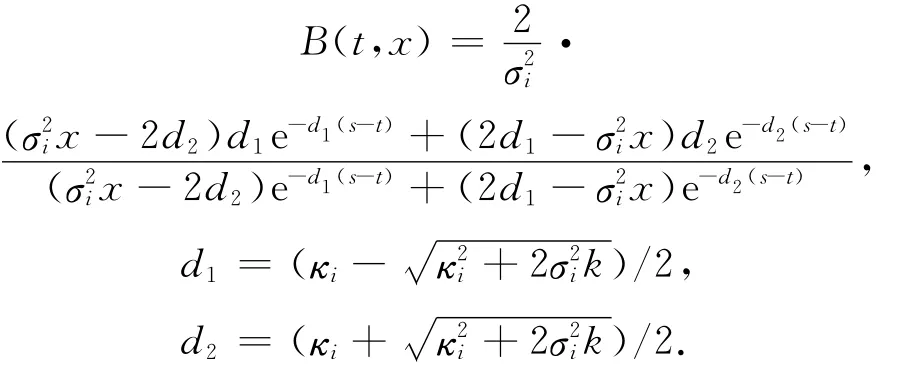
2.1.2 单因子反CIR模型的情形
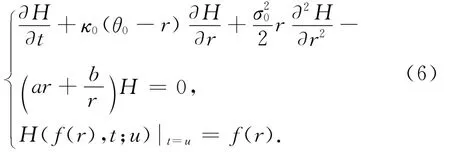
仿照文献[9]中的方法,最后可得方程(6)的解:

2.2 模型的非线性问题求解
将式(1)写成如下形式:
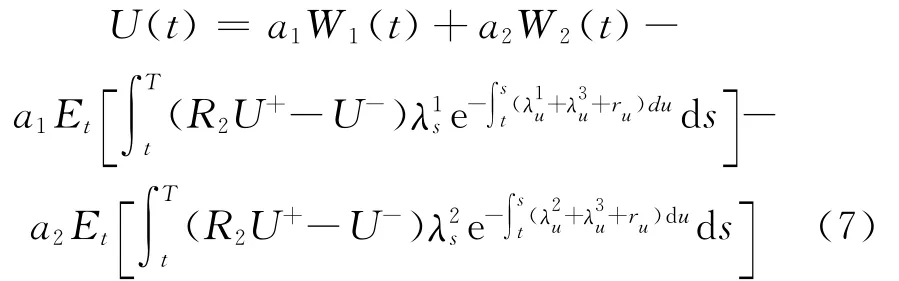
其中,W1(t)和W2(t)可以写成和H(f(r),t;u)的函数形式,而后一部分非线性条件期望利用Feynman-Kac公式后,得到非线性偏微分方程:

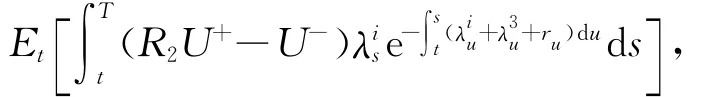
3 数值分析
利用第2.2节提出的迭代方法对含多交易对手的CDS合约的CVA值进行计算,迭代的具体方法是:将有方程右端的非线性项用不考虑交易对手违约的模型解析解代替,将方程变成一个线性方程组,该问题有第2.2节中得到的封闭解,然后将此解析解再代入方程右端的非线性项.这样反复,经过一定的迭代步数,就能得到yi(t)近似解,进而得到U(t)近似解.通过对结果的数值分析可得:① 验证迭代的收敛性以及收敛速度;② 考察系统风险因子对含多交易对手CDS合约的CVA的影响;③ 考察含多交易对手CDS合约的CVA与合约期限的关系;④分析含多交易对手的违约相关性对CVA值的影响,并与标准CVA进行比较.
本文图形中的基本对应参数取定如下:
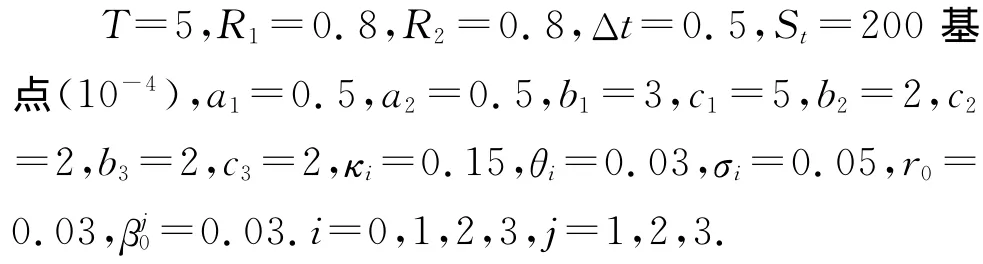
3.1 单因子CIR模型的情形
图2和表1都显示当迭代次数n≥5时,U(t)几乎不发生变化,说明了迭代的收敛速度非常快.即利用本文的模型计算CDS的CVA值有较高的效率.

图2 CDS价格关于约合期限T的关系Fig.2 The relationship between CDS price and T
图3和图4分别显示了含多交易对手单名CDS合约的CVA值与公共因子rt,合约期限T的关系.含多交易对手CDS合约的CVA值与合约期限正相关,且在T相对较小时CVA增长较快.这点说明,当合约期限较长时,交易对手违约的可能性增大,故
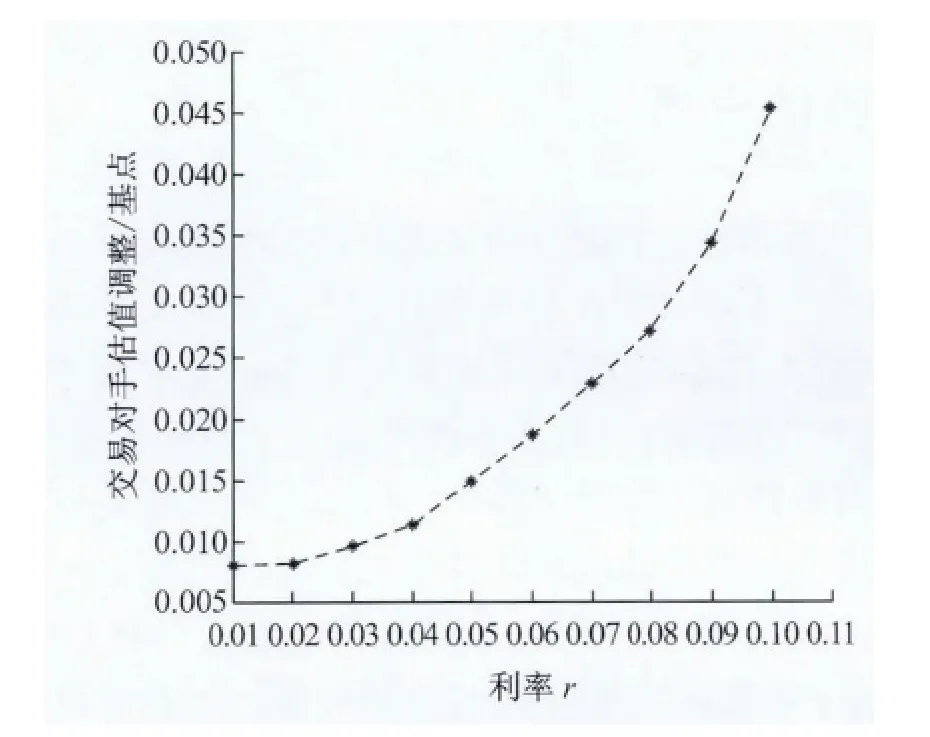
图3 CDS价格关于利率r的关系Fig.3 The relationship between CDS price and interest rate r
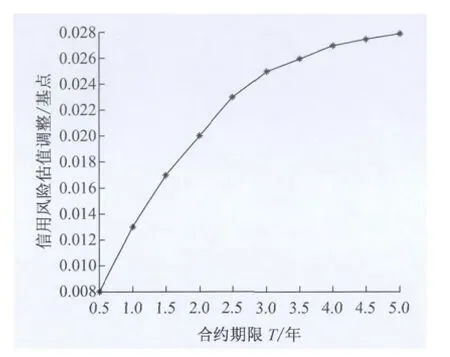
图4 CVA关于约合期限T的关系Fig.4 The relationship between CVA and T
CVA值相应增大.含多交易对手CDS合约的CVA值与利率亦正相关,利率增大时,表明整个市场收紧,违约风险加大,故CVA值也会增大;从图中也可看出,在利率较小时,CVA变化较小,反之亦然.
图5显示含多交易对手CDS合约的CVA值与合约卖方中B1和B2之间相关性的关系,含多交易对手CDS合约的CVA值与交易对手之间的违约相关性为正相关.即如果交易对手之间的相关性大,一旦其中一个交易对手违约则多交易对手都违约的风险也大,故其CVA值也会大.
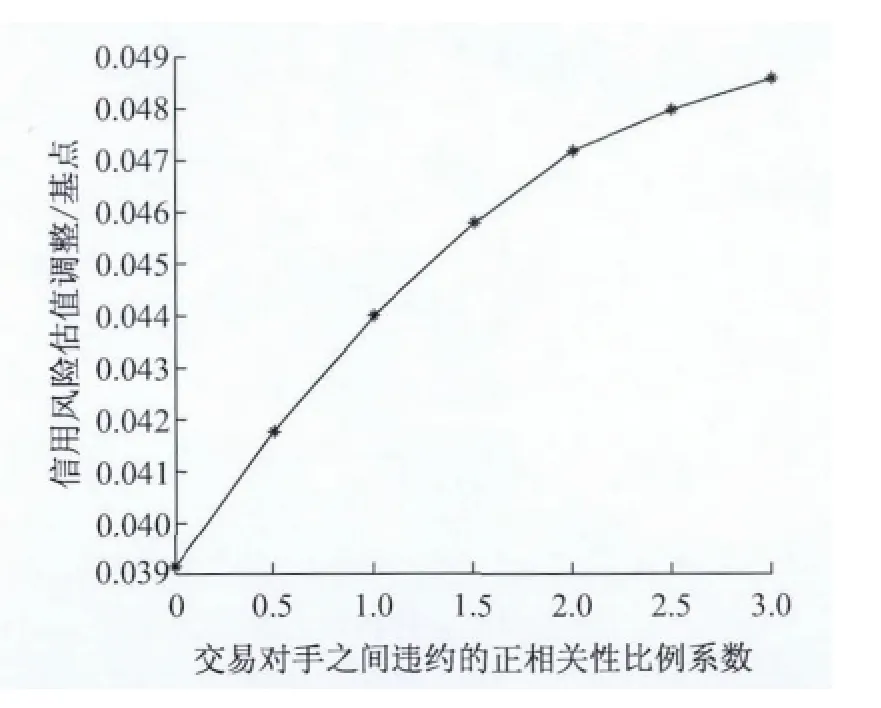
图5 CVA关于交易对手违约正相关比例系数的关系Fig.5 The relationship between CVA and correlation coefficient of counterparties
图6显示含多交易对手CDS合约的CVA值以及标准的CDS的CVA值与交易对手和参考公司之间的违约相关性之间的关系,它们都随着交易对手与参考公司之间违约相关性的增大而增大.这时交易对手和参考公司违约的可能性增大,故其CVA值也会增大,同时看到随着交易对手与参考公司之间违约相关性的增大,含多交易对手CDS合约的CVA值比标准的CDS的CVA值要小.
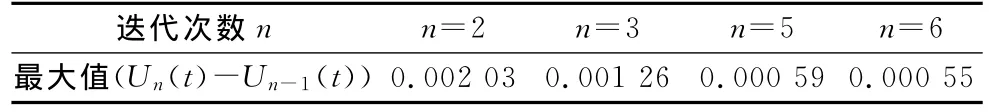
表1 CVA迭代差值与迭代次数之间的关系Tab.1 The relationship between iteration difference of CVA and the number of iterations
3.2 单因子反CIR模型的情形
图7显示含多交易对手的CVA值与合约卖方中B1和B2之间违约相关性为负情形下的关系.它们违约负相关性越大,CVA值越小.这时当一方交易对手违约的可能性增大时,另一方交易对手违约的可能性反而降低,故其CVA值减小.
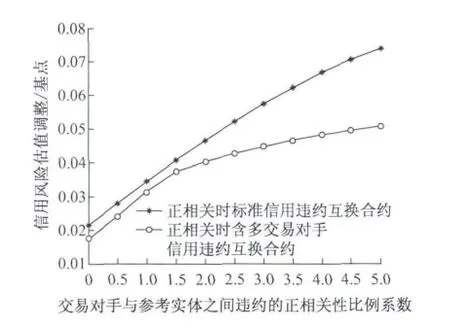
图6 CVA关于交易对手与参考实体违约的正相关比例系数的关系Fig.6 The relationship between CVA and the positive correlation coefficient of counterparty and the reference company
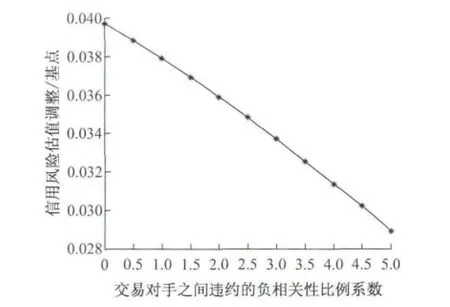
图7 CVA关于交易对手之间违约负相关比例系数的关系Fig.7 The relationship between CVA and the negative correlation coefficient of counterparties
图8显示含多交易对手单名CDS合约的CVA值以及标准CDS的CVA值与交易对手和参考公司之间的违约相关性之间的关系.
当交易对手都与参考公司间的违约为负相关时,含多交易对手单名CDS合约的CVA值随着交易对手与参考公司之间违约相关性的增大而减小,由于参考公司违约的可能性增大,则交易对手的违约可能性降低,其CVA减小.

图8 CVA关于交易对手与参考实体之间违约的负相关比例系数的关系Fig.8 The relationship between CVA and the negative correlation coefficient of counterparty and the reference company
当两交易对手与参考公司间的违约相关性一正一负时,含多交易对手的CVA值随着交易对手与参考公司之间违约相关性的增大而减小.即参考公司违约可能性增大,交易对手违约可能性此长彼消,但总体降低,其CVA减小.
从图中看出多交易对手的CDS与标准CDS的比较结果.在只要有交易对手间违约相关性一致时,标准CDS合约的CVA值比多交易对手CDS合约的CVA值要大,即此时多交易对手可以降低风险;而交易对手与参考公司违约相关不一致时,多交易对手的CDS合约的CVA值可能更大.
4 结论
本文研究了含多交易对手违约的单名CDS的CVA值的测算.通过分析考虑交易对手与参考公司之间违约的相关性,分别得到了三种不同单因子模型下CVA的计算模型,分别为多交易对手都与参考公司之间的违约相关性为正相关的情形;一个交易对手与参考公司之间的违约相关性为正相关而另一个交易对手与参考公司之间的违约相关性为负相关的情形;多交易对手都与参考公司之间的违约相关性为负相关的情形.它们的计算最终都化为非线性偏微分方程的数值解来表达.通过一个收敛速度较快的迭代算法,作了一些数值结果的分析,并且将结果与标准的单名的CDS的CVA值进行做比较分析,得到以下结果:
(1)交易对手与参考公司间违约的相关性为正时,多交易对手信用违约互换(CDS)合约的交易对手估值调整(CVA)值和标准的CDS的CVA值都随交易对手与参考公司间违约相关性的增大而增大,同时多交易对手的CVA值比标准的CVA值要小.即当交易对手与参考公司间的违约都是正相关时,相关性将加大风险,但多交易对手将降低风险.
(2)交易对手与参考公司间违约的相关性都为负时,多交易对手CDS合约的CVA值和标准CDS的CVA值都随着交易对手与参考公司之间违约相关性的增大而减小.即当交易对手与参考公司之间违约负相关时,相关性将降低风险.
(3)两交易对手与参考公司间的违约相关性一正一负的CVA值比两个都为负的CVA值要大;而标准的CVA值也比两个都为负的CVA值要大.即当交易对手与参考公司之间违约负相关时,另加负相关的交易对手将降低风险,而另加正相关的交易对手将增大风险.
致谢:感谢Anis Ben Brahim一起参与文章的讨论,并对文章提出了建设性的意见.
[1] Pykhtin M,Zhu S.A guide to modeling counterparty credit risk[J].Global Association of Risk Professional,2009,37:16.
[2] Alavian S,Ding J,Whitehead P,et al.Counterparty valuation adjustment(CVA)[J].The Annals of Applied Probability,2008,18(6):2495.
[3] Brigo D,Pallavicini A.Counterparty risk pricing under correlation between default and interest rates[J].Finance and Stochastic,2009(9):29.
[4] Brigo D,Pallavicini A.Counterparty risk and CCDSs under correlation[J].Risk,2008,3(2):84.
[5] Brigo D,Capponi A.Bilateral counterparty risk valuation with stochastic dynamical models and application to Credit Default Swaps[J].Risk,2012,7(2):141.
[6] Hui Li.Double impact on CVA for CDS:wrong-way risk with stochastic recovery[J].Annals of Combinatorics,2011,1(3):211.
[7] Wei W,Jiang L S.One fact CVA model for CDS with counterparty credit risk within the reduced form framework[J].International Journal of Financial Research,2012,2(2):68.
[8] LIANG Jin,WANG Tao.Valuation of loan-only credit default swap with negatively correlated default and prepayment intensities[J].International Journal of Computer Mathematics,2011,26:35.
[9] Ahn D H,Gao B.A parametric nonlinear model of term structure dynamics[J].Review of financial Studies,1999,12(4):721.
[10] Duffie D,Filipovic D,Schachermayer W.Affine processes and applications in finance[J].The Annals of Applied Probability,2003,13(3):127.

