大跨径曲线刚构桥曲率半径对其变形的影响研究

王 博

（唐山公路建设总公司 唐山 063000）

目前对大跨径直线连续刚构桥的受力特性已经研究得比较多，但对大跨径曲线连续刚构桥受力特性的研究还不充分。曲线连续刚构桥作为曲线桥梁的一种，由于存在“弯扭耦合”效应，其受力状况比直线型连续刚构桥复杂得多，本文以某地区大跨径曲线连续刚构桥为分析对象，对其曲率半径及其变形进行研究，旨在积累技术资料，促进大跨径曲线连续刚构桥的进一步发展。

某大桥引桥为预应力混凝土连续T梁，主桥为75.25 m＋140 m＋75.25 m连续刚构，位于半径R＝3 500 m的平曲线上。主桥梁体采用预应力混凝土变截面刚构连续箱梁，主墩采用钢筋混凝土双薄壁柔性墩。

1 有限元建模分析

1.1 有限元模型说明［1］

本文采用MIDAS CIVIL软件来分析建模，见图1。

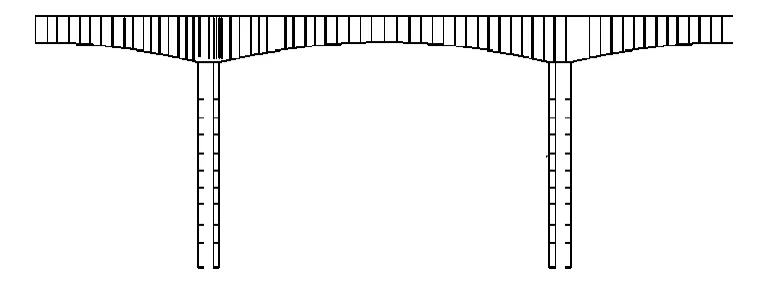
图1 结构建模简图

为了便于研究曲线连续刚构桥的静力特性，还假想并建立了曲率半径为2 500，1 500，500 m的弯箱梁。该弯箱梁除曲率半径与原箱梁的不一样外，其余包括跨径、材料、约束条件在内的各种参数，均与原弯箱梁完全一致。同时，还建立了一个直箱梁（曲率半径趋于无穷大）模型。通过有限元软件对箱梁模型进行比较，以期揭示各不同曲率半径的预应力混凝土连续箱梁在相同影响因素作用下，曲率半径对其变形的影响趋势。

曲线刚构桥主梁的弯曲程度是影响弯箱梁桥受力特性的最重要因素。曲率半径相同时跨径越大弯曲程度越大，考虑到曲率半径不能全面地反映其弯曲程度，因此，将反映主梁弯曲程度的参数定为跨长同半径的比值。建模时固定弯箱梁桥的跨径不变，即跨径布置为：75.25 m＋140 m＋75.25 m，曲率半径则分别为500，1 500，2 500，3 500 m和直线刚构桥（曲率半径无穷大）。通过建立5种曲率半径的桥梁有限元模型来计算分析曲线刚构桥在不同曲率半径下的结构的反应。

1.2 模型弯扭变形的度量方法

曲线桥在荷载作用下，由于弯扭耦合作用，外侧节点的挠度大于内侧节点的挠度，为了量化预应力混凝土箱梁的扭转变形，特意制定了以下方法：

桥面中心线节点i处的挠度用z0表示（以向上为正），结点i内侧的挠度用z1表示（以向上为正），结点i外侧的挠度用z2表示（以向上为正），桥面宽度用L表示，见图2。

图2 弯扭变形度量示意图

从图2可以看出，假设弯箱梁上的扭转角为a1，则有

节点i外侧挠度：

节点i内侧挠度：

α1为该结点i的扭转角，这个扭转角代表了桥面上结点i与曲率中心连线所在的桥面直线的平均扭转角，可以认为该扭转角可以反映出该位置桥面的实际扭转情况。通过研究桥梁各个位置扭转角α的数值，即可了解整个桥梁各截面的扭转变化情况。

2 悬臂状态荷载作用下曲率半径对弯梁变形的影响

曲线刚构桥采用挂篮悬臂施工，在荷载作用下，曲率半径是否对其受力有影响值得研究。在悬臂状态，为研究曲率半径对曲梁受力的影响，从宏观和局部两方面进行分析［2］。

经过模型分析计算，发现悬臂状态下曲率半径并未改变内力及变形最大值的位置。悬臂状态内力最大值在悬臂根部，变形最大值在距离悬臂端L／5处。

根据计算分析，不同曲率半径的弯刚构在各个施工阶段的内力分布基本相同。不同曲率半径的同一纵向位置节点号相同，节点号在桥梁半个悬臂端，悬臂刚构桥在施工过程中，荷载作用下的挠度值倍受关注。曲线刚构桥施工过程中，曲率对弯梁变形值的影响程度值得探究。

对于箱梁桥面中心线的挠度，用有限元软件分析得到的挠度数据见图3。

图3 最大悬臂状态不同曲率半径下箱梁中心线挠度比较图

由图3可见，不管曲率半径为何值，荷载作用下，都是42号节点变形最大，该位置大概在距离最大悬臂端L／5处。在墩梁固节处，其变形值较小，这说明桥墩竖向压缩主要是由梁体荷载造成的。曲率对连续刚构的竖向变形的影响是非常明显的。其变化规律为：随着曲率的增加，其竖向变形越来越大。而最大悬臂状态荷载作用下箱梁节点扭转情况见图4。

图4 最大悬臂状态不同曲率半径下箱梁节点扭转角曲线图

由图4可见，最大悬臂状态荷载作用下，悬臂根部扭转角最大。对小半径曲线刚构桥，其悬浇段立模标高的确定需要对扭转角进行修正，否则由于扭转变形的累计，会导致成桥线形显著偏离设计理想状态。

3 营运阶段活载作用下曲率半径对弯梁变形的影响

连续刚构桥在活载作用下，将产生一定程度的下挠。当刚构桥存在曲率半径时，活载作用下曲率半径对挠度的影响值得探究。活载作用下曲率半径对挠度的影响非常敏感，曲率半径越小，活载作用下的挠度值越大。这是由于曲线桥在活载作用下，“弯扭耦合效应”使得桥梁挠度比直线桥大［3－4］。因此，在桥梁设计中，曲线桥在活载作用下的挠度无法用直线桥模拟。活载作用下，曲线刚构桥将产生扭矩，主梁将产生扭转，使得主梁内外侧挠度不等，内外侧挠度计算可参考公式1与2。活载作用下扭转角见表1。

表1 成桥状态活载作用下扭转角变化情况表 rad

成桥状态活载作用下，中跨跨中扭转角最大，根部扭转角最小，与悬臂状态荷载作用下扭转角的最大与最小位置相反。曲率半径500 m的刚构桥的最大扭转角为0.000 369 766 rad，由此引起的曲线内外侧标高差为0.9 c m；直线桥的最大扭转角为0.000 270 717 rad，由此引起的曲线内外侧标高差为0.75 c m。可以看出，挠度与曲率半径用对数函数能较好地模拟，随着曲率半径的增加，挠度数值越来越小。

4 结语

本文依托工程的基本情况并建立了曲率半径分别为500，1 500，2 500，3 500 m及直线刚构桥的有限元模型，研究了曲线刚构桥施工变形规律。对预应力混凝土曲线刚构桥的受力进行了研究、分析，通过对改变主梁曲线半径的对比计算，可以看出：

（1）变形与曲率半径呈对数关系变化。

（2）曲线刚构桥在悬臂状态施工，曲率半径对受力最不利及挠度最大值的位置没有影响，其中悬臂阶段挠度最大值位于距悬臂端L／5处。

（3）曲率半径越小，曲率内外侧标高差值越大，小半径连续刚构桥在进行悬浇施工时必须对其立模标高进行扭转角修正。

（4）活载作用下曲率半径引起曲梁的内外侧挠度差可忽略不计，但对竖向挠度影响明显，无法用直线桥模拟。当曲率半径为2 500 m以下时，挠度值至少增加30%。

［1］ 马保林.高墩大跨连续刚构桥［M］.北京：人民交通出版社.2007.

［2］ 王雄江.曲线箱梁桥空间分析及程序设计［D］.武汉：武汉理工大学，2003.

［3］ 邵容光.混凝土弯梁桥［M］.北京：人民交通出版社，1996.

［4］ 王钧利，贺拴海.高墩大跨径曲线刚构桥设计参数与稳定分析［J］.武汉理工大学学报：交通科学与工程版，2005（5）：717-720.