模糊神经Petri网算法优化及其收敛性分析
李孝忠,周艳军
(天津科技大学计算机科学与信息工程学院,天津 300222)
模糊神经 Petri网(fuzzy neural Petri net,FNPN)是将 Petri网与模糊理论相结合,并引入神经网络算法而提出的.目前,已有针对 FNPN的相关研究,文献[1]提出了一种基于BP算法的无回路模糊Petri网(fuzzy Petri net,FPN)模型的自学习推理算法,使得网络具有很好的泛化和自适应能力,但是网络震荡趋势较大;文献[2]采用基于专家经验的系统结构,提出了一种适合于可靠性估计的 FNPN模型,其既可以表示模糊产生式规则的知识库系统又具有学习能力,但是并没有考虑到网络震荡性的问题;文献[3]提出一种自适应 FPN,通过对变迁点燃条件的判断及变迁点燃后传递给输出库所的新标记,建立 S型连续函数并引入 BP算法,实现了对知识的动态推理及学习,但是没有在专家系统方面进行预测;此外,FNPN在故障诊断[4–7]方面的应用研究也存在收敛慢或震荡较大等问题.
本文提出一种适合于基于专家经验系统结构的FNPN模型的参数修正优化算法,即在传统 BP神经网络参数修正公式中加入新型动量项[8],从而达到改善学习收敛速度、提高计算精确度并减小网络震荡的效果.
1 模糊神经Petri网
1.1 模糊神经Petri网的定义
Petri网[9–10]是由库所、变迁和连接库所与变迁间关系的有向弧组成的一种有向图.一般地,图中表示位置用圆圈,表示变迁用直线段或矩形框,位置与变迁间的关系用有向弧连接.
定义1 模糊Petri网[1]定义为九元组
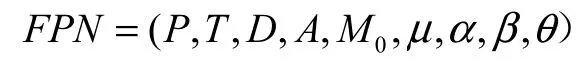

定义2 模糊神经Petri网[2]定义为十二元组的含义同定义 1;0:M P→[0,1]为初始模糊标识;Kp为隐含层和输出层库所的活动状态集;Kt为变迁集T到规则集的一一映射;
其中:为置信度集合,它与每个变迁一一映射.
1.2 模糊神经Petri网模糊产生式规则
模糊产生式规则[1]中的简单规则和“与”规则均对应 FNPN中的一个变迁,而一条“或”规则对应 FNPN中的一组变迁,模糊产生式规则中的命题与 FNPN中的库所是一一对应的,规则中模糊命题的当前隶属度值为 FNPN中库所的标记值,规则的置信度和阈值对应 FNPN中变迁的一个映射函数,规则中的权值对应 FNPN中相应变迁的输入有向弧上的权值.简单规则、“与”规则及“或”规则对应的FNPN模型类似于文献[1]中的定义2.
1.3 模糊神经Petri网的使能条件
对于一个变迁jtT∈,若为库所ip 的标识,i=1,2,…,m,j=1,2,…,n,称变迁jt是使能的.都有,其中
1.4 模糊神经Petri网的变迁规则
使能的变迁可以点燃,当变迁 t点燃时,其输入库所中的标记值不改变,而向输出库所传送新的标记值,新标记的计算规则如下.
对于图 1所示的模糊产生式简单规则[1],输出库所2p将获得新标记值2()Mp′,计算规则为


图1 简单规则的FNPN模型Fig.1 FNPN model of simple rules
对于图2所示的模糊产生式“与”规则[1],输出库所 pm将获得新的标记值计算规则为

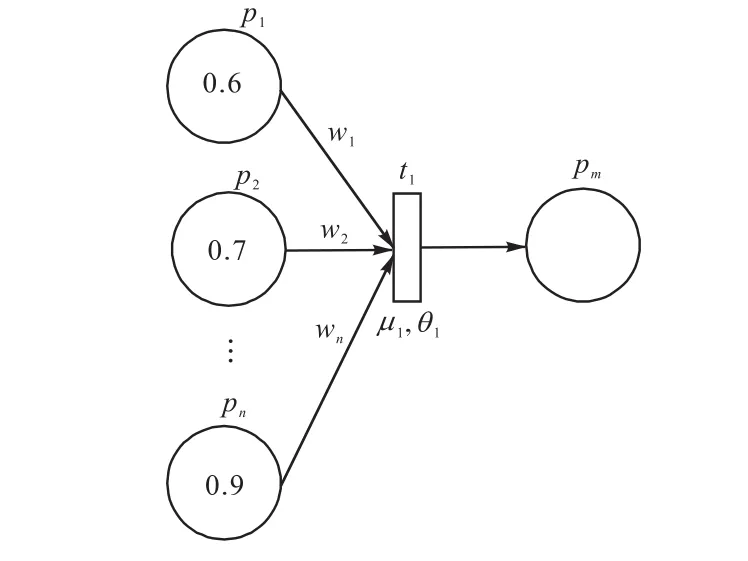
图2 “与”规则的FNPN模型Fig.2 FNPN model of“and”rules
对于图 3所示的模糊产生式“或”规则[1],输出
库所 pm将获得新的标记值计算规则为
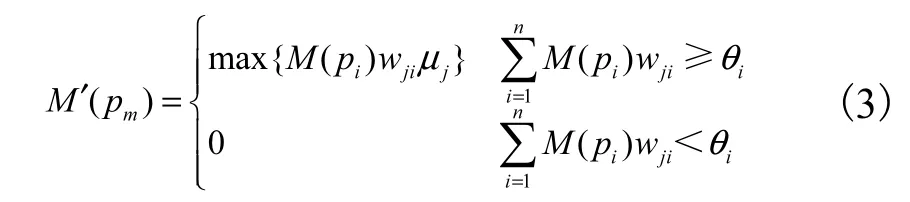

图3 “或”规则的FNPN模型Fig.3 FNPN model of“or”rules
2 FNPN算法优化改进
2.1 引入S型函数
针对FNPN模型中变迁的使能条件及FNPN的样本数据学习训练中的特点,采用 2种 S型连续函数分别表示变迁使能及变迁点燃后的新标记值.

2.2 增加新型动量项
为了改善网络的收敛特性,在增大学习率的同时不至于产生震荡,在传统的权值、置信度及阈值修正公式[8]中增加一个新型动量项,即

2.3 实例说明
以上内容对 FNPN模型的相关定义和算法改进之处进行了描述,为了更加清晰明确的阐述其中涉及的公式计算,特别列举一实例加以说明.
现假设有一个专家系统[11]R,系统中命题集为其模糊产生式规则如下:
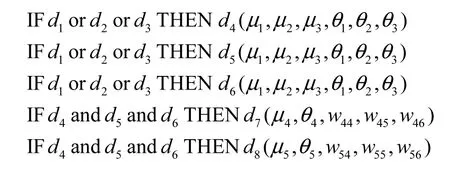
其中
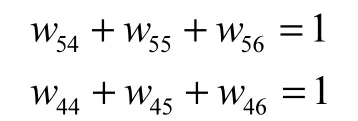
该专家系统R对应的FNPN模型如图4所示.
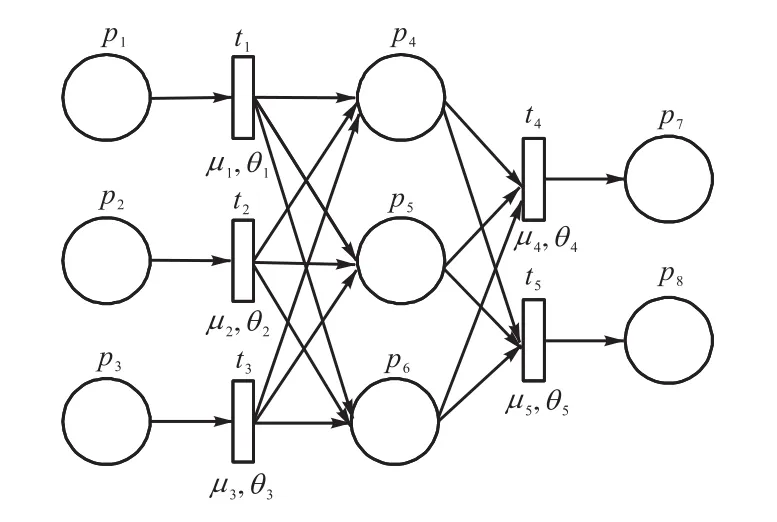
图4 专家系统R的FNPN模型Fig.4 FNPN model of expert system R
FNPN模型为

式中:

假设图 4中初始输入库所的标记值分别为 0.9、0.8、0.95,变迁的置信度分别为 0.7、0.9、0.8、0.95、0.98,阈值分别为 0.6、0.7、0.7、0.72、0.65,初始权值为
(1)判断变迁1t、2t和3t的使能状态.库所1p传递标识给1t后,利用函数1()Fx判断1t的使能状态,经计算可知当常数b足够大时即变迁1t是使能的.同理可知,变迁2t和3t也是使能的.
(2)计算库所4p、5p和6p的标记值.对于4p,
(3)判断变迁4t和5t的使能状态.4p、5p和6p传递标识给4t后,利用函数1()Fx判断4t的使能状态,计0.76,同理可计算得算可知且当常数b足够大时即变迁4t是使能的.同理可知,变迁5t也是使能的.
(4)计算最终输出库所7p和8p的标记值. 对于7p,0.2166,同理可计算得
3 改进的FNPN算法步骤及其收敛性分析
3.1 改进的FNPN算法步骤[2,12-13]
(1)对系统设置初始值,将所有输入权值、变迁置信度以及节点阈值的初始值设置为较小的随机数,令输入命题和中间命题的总个数为m,变迁的总个数为n,样本总数为N,i和 j分别为1.
(2)由设计思路自动生成目标函数f,并规定误差限ε.
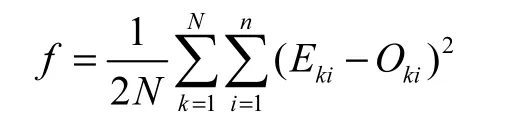
(3)输入随机样本数据以及期望输出、函数1()Fx和2()F x的各常数值,根据1()Fx的判断结果,对使能的变迁 t利用2()F x计算实际输出,得到初始误差,若0fε<,则结束;否则就直接进入下一步.
(4)依据式(5)对权值进行调整,并且判断是否每一个权值都大于等于零,若权值都大于等于零,转(5);否则,转(6).
(5)依据调整后的权值,重新计算得到的误差值,比较误差值if与1if−,若则转至(4);否则进入下一步.
(6)改变动量因子α 的值,重新调整权值,说明原来的权值调整方式不正确.
(7)令 1ii=+ ,判断 i是否大于 n,若不大于则转(3),否则转入下一步.
(8)判断此时的if是否已经达到规定的误差限,若已经达到,则终止训练;若还没有达到,判断权值训练次数是否超过规定次数,若没有,则将if赋值给并重新使得 i=1,转(3),开始下一轮的训练;如果已经超过了规定的训练次数,则转(9).
(9)对变迁的置信度进行训练,逐个调整置信度,使其不超过 1,逐次计算误差值kf并判断是否达到误差限,若达到误差限,则终止训练;若还没有达到,则一直调整置信度直到达到规定的训练次数为止;如果此时还没有达到要求,则转(10).
(10)同步骤(9)对节点阈值进行训练.
3.2 收敛性分析
定理 对于式(5)的 FNPN 调整公式,当t→∞时,r∀∈N都有即按照此算法调整网络是收敛的.
当r=1时

根据范数的齐次性有

此式显然存在如下关系式:

因此是收敛的.
假设r=k时公式收敛,即

根据范数的性质,对于0ε∀>,2n∃∈N,都有

则当r=k+1时,有
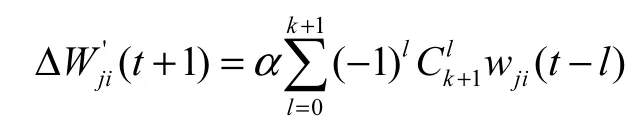
亦即
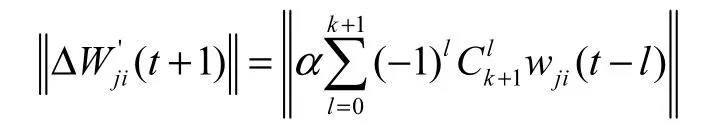
进而有

根据范数的三角不等式性质有


根据两面夹定理有

综上所述,可知0ε∀>,t→∞都有

亦即调整算法是收敛的.
4 结 语
本文提出的 FNPN优化算法利用带有不同参数的S型函数不仅使得FNPN学习训练过程变迁t使能状态的判断更快捷、变迁点燃后传递给输出库所的新标记值结果更精确;而且在训练过程中为了改善网络的收敛特性,在增大学习率的同时不至于产生震荡,在传统的参数修正公式中引入动量项,对网络中的权值、阈值及置信度进行修改,经过证明此调整算法是收敛的.
针对优化算法精确度、收敛性及网络震荡趋势的数据和图像方面的展示证明还有待进一步阐述.
[1] 鲍培明. 基于 BP网络的模糊 Petri网的学习能力[J].计算机学报,2004,27(5):695–702.
[2] 原菊梅,侯朝桢,王小艺,等. 复杂系统可靠性估计的模糊神经 Petri网方法[J]. 控制理论与应用,2006,23(5):687–691.
[3] Li Xiaoou,Yu Wen,Lara-Rosano F. Dynamic knowledge inference and learning under adaptive fuzzy Petri net framework[J]. IEEE Transactions on Systems,Man and Cybernetic,Part C:Applications and Reviews,2000,30(4):442–450.
[4] 刘静,潘炼. 基于模糊 Petri网的高炉故障诊断系统[J]. 计算机测量与控制,2013,21(5):1157–1159.
[5] Binh P T T,Tuyen N D. Fault diagnosis of power system using neural Petri net and fuzzy neural Petri net[C]//Proceedings of 2006 IEEE Power India Conference. Piscataway:IEEE,2006,554–558.
[6] 张智泉. 基于模糊神经Petri网的绝缘子运行状态诊断系统研究[D]. 武汉:湖北工业大学,2011.
[7] 徐辉. 基于模糊神经 Petri网的高炉故障诊断[D]. 武汉:武汉科技大学,2012.
[8] Li Xiaozhong,Li Qiu. A parameter adjustment algorithm of BP neural network[C]//Proceedings of the 3rd International Conference on Intelligent System and Knowledge Engineering. Piscataway:IEEE,2008:892–895.
[9] Ahson S I. Petri net models of fuzzy neural networks[J].IEEE Transactions on Systems,Man and Cybernetics,1995,25(6):926–932.
[10] 方平. 基于Petri网的知识表示方法研究[D]. 武汉:武汉理工大学,2013.
[11] Liu Xin,Yin Guisheng. Fuzzy neural Petri nets for expert systems[C]//Proceedings of the 2nd International Conference on Intelligent Computing Technology and Automation. Piscataway:IEEE,2009:732–735.
[12] Wai R J,Chu C C. Motion control of linear induction motor via Petri fuzzy neural network[J]. IEEE Transactions on Industrial Electronics,2009,54(1):281–295.
[13] Hanna M M,Buck A,Smith R. Fuzzy Petri nets with neural networks to model products quality from a CNC-millings machining center[J]. IEEE Transactions on Systems,Man and Cybernetics,Part A:Systems and Humans,1996,26(5):638–645.

