基于MATLAB的某大口径榴弹发射器的变初速分析

高建彪

（中北大学 机电工程学院，山西 太原 030051）

0 引言

随着恐怖主义给人们带来的伤害不断加剧，国际社会也加强了对反恐作战的研究。针对反恐作战的特殊性，反恐作战所使用的武器需要对不同距离的目标发射不同初速的弹丸，控制弹丸毁伤效能，根据实际情况做到致命与非致命效果的选择。本文以某大口径榴弹发射器为例，对外加药室容积变初速方式进行分析。运用无后坐炮理论和枪炮内弹道原理，对某大口径榴弹发射器的变初速内弹道机理进行研究，建立其内弹道数学模型，通过MATLAB仿真计算软件，编写计算程序进行仿真计算，分析计算结果和曲线图，以了解外加药室容积的位置对弹丸初速影响的变化规律。

1 某大口径榴弹发射器内弹道数学模型

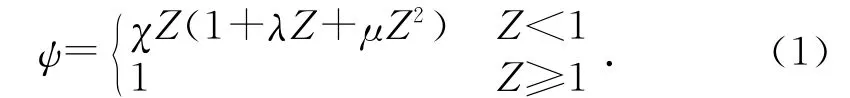
其中：ψ为火药已燃相对质量；Z为火药已燃相对厚度；λ，χ，μ均为火药形状特征量，χ＝1＋e1／c，λ＝－（e1／c）／（1＋e1／c），c为火药长度，e1为火药1／2厚度。

（2）火药正比燃烧速度方程：

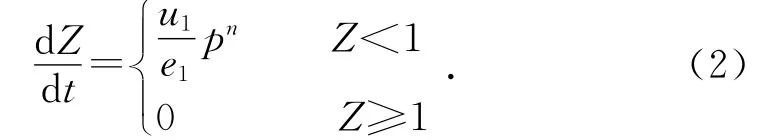
本文运用枪炮内弹道学原理作为理论基础，对榴弹发射器发射榴弹的内弹道过程进行理论分析。为方便计算，需要对内弹道过程加以合理的简化和假设，从而建立起内弹道方程组，将枪管长度、枪口截面面积、弹丸质量与弹药装填方式联系起来。根据该榴弹发射器本身内弹道的特点，按照理想的条件进行建模。

（1）内弹道模型的几何燃烧定律方程：

其中：u1为火药燃烧的线速度；p为膛内压力；t为时间。（3）弹丸行程方程：

其中：l为弹丸行程；v为弹丸速度。（4）弹丸速度方程：

其中：S为膛口截面面积；φ为次要功计算系数；m为弹丸质量。

（5）膛内压力计算方程：

其中：f为火药力；ω为装药量；lψ为药室自由容积缩颈长；k为绝热指数。

（6）药室自由容积缩颈长计算方程：

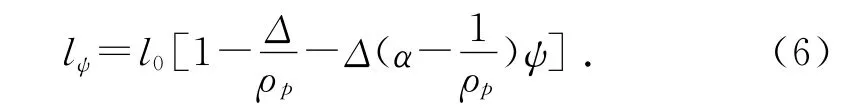
其中：Δ＝ω／V0为火药装填密度，V0为药室容积；α为火药燃气余容；ρp为火药密度；l0＝V0／S为药室容积缩颈长。

综合式（1）～式（6）即得内弹道方程组：

2 外加药室容积的变初速技术

2.1 外加药室容积变初速方式的理论基础

变初速的技术有多种多样，本文所采用的是外加药室容积技术。外加药室容积是指在弹膛外加装一个密闭容积，增加火药燃气膨胀空间。当弹丸经过外加药室容积时，一部分火药燃气迅速流入药室，火药燃烧空间瞬间增大，膛内压力急剧下降。膛内压力计算方程表明，膛压与药室容积缩颈长呈负相关，即药室容积缩颈长的数值越大，弹丸受到的平均膛压就越小，而外加药室容积恰恰增加了药室容积缩颈长，从而降低了平均膛压。根据牛顿第二定律，弹丸的加速度和弹丸在膛内受到的平均膛压呈正相关。以上述理论为基础可知，增加药室容积缩颈长，就可以降低平均膛压，减小弹丸的加速度，进而降低弹丸的速度。

2.2 外加药室容积变初速方式的内弹道模型

在原内弹道模型和基本假设基础上，在原药室容积V0基础上增加了一定量的药室容积后，式（6）变为：

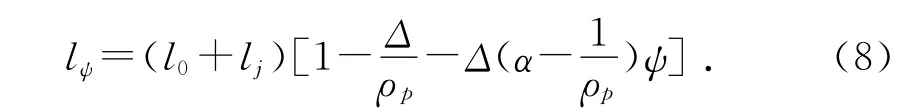
其中：lj为外加药室容积缩颈长。假设在理想的条件下进行建模，在原内弹道模型基础上的外加药室容积变初速方式的内弹道数学模型为：

3 采用外加药室容积变初速技术的内弹道仿真

根据外加药室容积变初速发射技术的基本理论，假设外加药室的容积为Vj＝10 cm3，把外加药室容积分别布置在距膛底2 mm、10 mm、20 mm、30 mm、40 mm处，计算外加药室容积在不同位置时对弹丸初速的影响。在MATLAB环境下编写相应的程序，计算得出膛压与弹丸行程曲线见图1、弹丸速度与时间曲线见图2。

由图1可知，随着外加药室容积位置向枪口方向移动，膛内压力下降速率在减小。这是因为外加药室容积的位置越靠近枪口，膛内火药燃气到达外加药室容积所需时间就越长，损失的火药气体能量就越少，因此外加药室容积和枪口的距离越近，对膛压的影响越小。

图1 膛压与弹丸行程曲线图

图2 弹丸速度与时间曲线图

由图2可知，外加药室容积和枪口的距离越近，弹丸速度下降得越少。因为随着外加药室容积向枪口靠近，弹丸在到达外加药室前获得的加速度就越大，从而获得较高的初速，因此外加药室容积和枪口距离越近，对弹丸的初速影响就越小。

4 结论

本文以某大口径榴弹发射器为研究对象，并应用经典内弹道理论，建立了内弹道模型。对外加药室容积时的内弹道进行仿真计算，在MATLAB环境下，得到膛压与弹丸行程曲线图、弹丸速度与时间曲线图；得出外加药室容积在不同位置时对膛压和弹丸初速的影响规律，即外加药室容积距离膛底越近，弹丸的初速越低。

［1］ 金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004.

［2］ 姚养无.火炮与自动武器动力学［M］.北京：兵器工业出版社，2000.

［3］ 薛定宇，陈阳泉.高等应用数学问题的 MATLAB求解［M］.北京：清华大学出版社，2004.