弹膛开槽对枪机运动规律影响的仿真分析

廖 辉，王 刚，张小石，杨 卓

（中北大学 机电工程学院，山西 太原 030051）

0 引言

手枪、冲锋枪等自动武器普遍采用自由枪机式自动方式，用火药气体的能量来推动枪机后坐。设计过程中为降低全枪质量，采用了质量相对较小的枪机。然而质量较小的枪机导致枪机后坐速度过大，后坐到位的撞击能量也会过大，影响连续射击时的准确性。一般采用膛内开槽的方法来降低枪机后坐速度，由于采用传统的数学计算方法难以得到准确的数值解，因此本文采用有限元软件来分析膛内开槽对枪机运动规律的影响。

1 自由枪机式自动方式

自由枪机式自动方式是指没有专门的闭锁机构，仅靠枪机的惯性和复进簧力使枪弹在弹膛处于闭而不锁的状态。枪机在膛内火药燃气压力增大到弹头开始启动时开始后坐，应确保在膛压较高时弹壳后移量很小，避免弹壳在膛压较高时退到枪管外部导致炸裂［1］。自由枪机式武器要求弹壳长度短、最大膛压低、发射弹头质量小。为减小枪机后坐速度，可以采用膛内刻螺旋槽或凹槽的方式增加后坐阻力，或采用前冲击发以抵消一部分后坐能量，或者增加枪机质量也可以取得一定的效果。

2 模型建立

2.1 内弹道模型

首先利用经典内弹道理论编写内弹道程序，得到膛压曲线［2］。主要内弹道公式为：

其中：l为弹丸位移；t为时间；v为弹丸速度；S为弹膛横断面积；φ为次要功系数；m为弹丸质量；p为膛内平均压力；Z为火药粒已燃相对厚度；u1为火药粒燃烧速度；e1为1／2火药粒厚度；n为燃速指数；lψ为药室自由容积缩颈长；f为火药力；ω为装药质量；ψ为火药形状函数；θ为火药热力系数；χ，λ，μ均为与火药粒形状尺寸相关的特征量；l0为药室容积缩颈长；Δ为火药填装密度；ρp为火药密度；α为余容。

再利用半经验公式（2）推导膛底压力pT，得到如图1所示的膛底压力曲线：

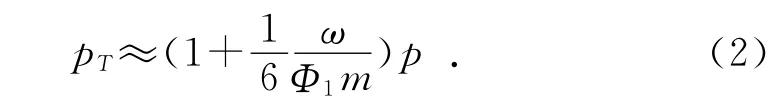
其中：Φ1为弹丸质量虚拟系数，此处取值1.05。

由图1中可看到，膛底压力在0.12 ms时达到最大值227 MPa，然后迅速下降，在2 ms后膛压下降到可以忽略的程度。

2.2 虚拟样机计算模型

本虚拟样机的主要构件有3个，分别为弹膛、枪机和弹壳［3］。结合模型轴对称的特点，为减少计算量，只取模型的1／4进行建模。在UG中完成该枪弹膛、枪机和弹壳的建模，再将模型导入ABAQUS中。在模型的对称面上施加对称约束；由于不考虑枪机变形对分析的影响，对枪机施加刚体约束，为枪机运动添加带有弹性的运动副，用于模拟复进簧的作用，运动摩擦系数取为0.09；其余模型采用通用接触设置，摩擦系数为0.11。

以某手枪为例，该枪采用9 mm手枪弹，弹壳为无凸缘的筒形弹。弹壳材料为覆铜钢，材料塑性特性简化为双折线，比例极限为235 MPa，强度极限为358 MPa，塑性应变为0.5，采用弹壳口部定位的方式。在弹壳内表面施加大小为pT的压强载荷曲线用于模拟火药压力。

对弹壳和弹膛模型划分六面体网格，单元类型为C3D8I。外形较为复杂的枪机采用四面体自由网格，单元类型为C3D10M。这两种单元类型对显式动力学分析中的应力问题的模拟较好［4］。划分网格后的模型见图2。

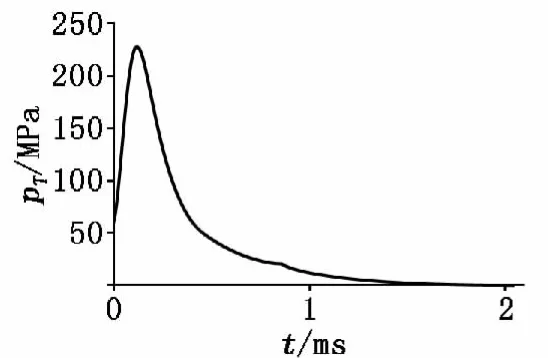
图1 膛底压力曲线

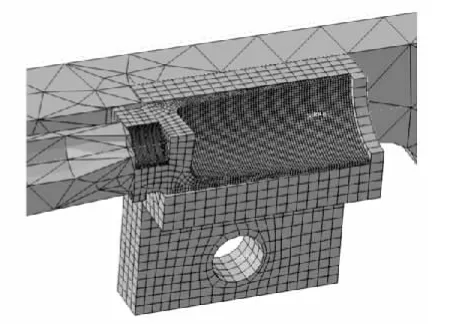
图2 划分网格后的模型

参照某手枪的开槽参数，再建立一个膛内开槽模型。设定开槽最大深度为0.1 mm，槽边缘倒半径为5 mm的圆角与弹膛后段圆滑过渡，最大槽深处距枪膛尾端面距离为5 mm，开槽模型的其余参数与未开槽模型一致。弹膛内开槽后的模型如图3所示。

3 弹壳运动理论分析

弹壳与弹膛的应力－应变关系见图4。在膛压上升阶段，弹壳径向膨胀，在走完弹壳与弹膛的间隙OB′后弹壳开始挤压弹膛。膛压达到最大值pM时，弹壳与弹膛共同膨胀到A位置，此时壳膛间作用力最大，抽壳阻力也最大。膛压下降阶段，由于弹壳材料的弹性模量与弹膛材料弹性模量相近，因此其恢复线与弹膛的弹性恢复线平行。当膛压下降到可以忽略时，弹膛恢复至B′位置，弹壳恢复至f′位置，壳与膛之间仍有过盈量B′f′存在。弹壳在达到弹丸启动压力时就开始向后运动，运动过程中要克服抽壳阻力并推动枪机后坐，直到弹壳完全从弹膛中抽出，弹壳运动过程见图5。

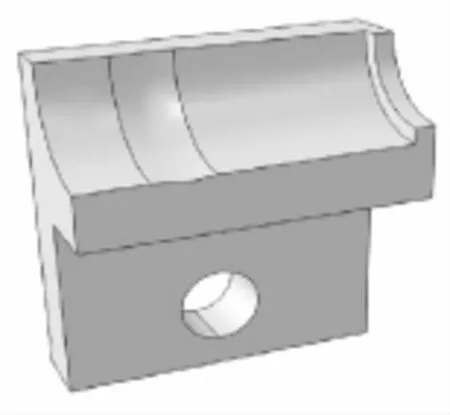
图3 弹膛内开槽模型

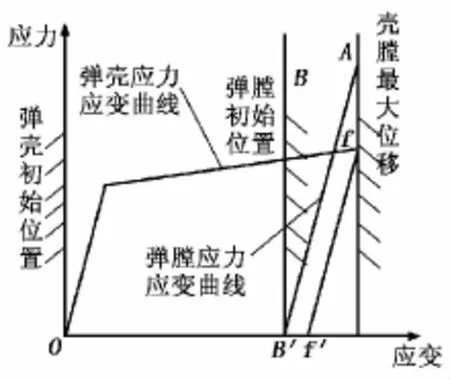
图4 弹壳与弹膛的应力－应变关系

图5 弹壳运动过程

4 仿真结果

4.1 枪机后坐速度

膛内未开槽时和开槽后枪机的后坐速度见图6。由图6可以看出：膛内未开横时枪机最大后坐速度为8.51 m／s；膛内开槽后，由于弹壳后坐阻力增大，枪机最大后坐速度下降到7.31 m／s，即速度下降了14.1%。根据得到枪机动能下降26.2%，故膛内开槽可以有效降低枪机后坐速度，减小后坐能量。

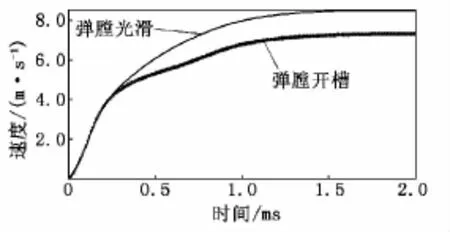
图6 枪机后坐速度对比

4.2 抽壳阻力变化曲线

提取结果中摩擦力与沿轴向接触力的合力再乘以4，得到该弹壳抽壳阻力如图7所示。抽壳阻力的变化趋势与膛压曲线变化趋势相似，最大抽壳力在开槽前、后基本保持不变，约7 000 N。开槽后由于接触表面外形变化，抽壳阻力出现较明显振荡，总体趋势较光滑弹膛时下降慢。抽壳阻力将大量动能转化为内能，有利于减慢枪机的后坐运动速度。

5 结论

采用膛内开横槽方法在使用小质量枪机的情况下，可以显著降低自由枪机式武器的枪机后坐速度，并减小枪机后坐到位时的撞击能量。同时由于最大抽壳阻力也能保持基本不变，因此保证了开槽后抽壳动作的可靠性。

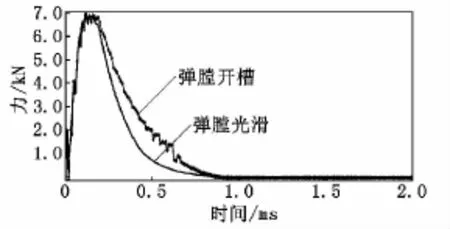
图7 抽壳力对比

［1］ 欧学炳，殷仁龙，王学颜.自动武器结构设计［M］.北京：北京理工大学出版社，1995.

［2］ 宋广惠，王学颜.射击过程中壳机力与抽壳力的计算机仿真［J］.南京理工大学学报，1994（6）：41－46.

［3］ 康艳祥，张以都，白昭鹏.自动武器抽壳力仿真及抽壳力相关研究［J］.计算机仿真，2007（3）：18－22.

［4］ 徐耀春.舰炮抽壳系统非线性结构动力学分析［D］.镇江：江苏科技大学，2011：66－70.