直冷却通道斜置肋片传热特性的数值研究
张艾萍,付 磊,杜五一
(东北电力大学能源与动力学院,吉林 长春 132012)
1 引言
燃气轮机中,随着轮前燃气温度的提高,涡轮叶片承受的热传导也随之增大,严重影响涡轮运行的安全性和稳定性。改进涡轮叶片的冷却方式和冷却结构,以满足涡轮稳定运行的要求,是解决叶片受热问题的主要手段之一。而掌握冷却通道传热分布规律,进而改进和优化叶片内部冷却通道结构,对提高叶片受热能力具有重要意义。
对于加置肋片、强化换热,很多学者都做了大量的实验研究和数值模拟。Han等[1]对有周期性肋片的矩形直通道中的换热与流动性能进行了实验研究,发现方形通道中肋片斜置角度α为30°~45°时的换热效果比横肋的换热效果提高约30%。Park等[2]研究了五种不同宽高比的情况,对于方形通道,当肋片斜置角度为45°时有最好的强化换热效果。Hsieh等[3]研究了方形带肋直通道的换热效果,并给出了努赛尔数与雷诺数之间的经验关系式。Stephens等[4]研究了斜肋对换热效果的影响,发现换热效果受肋的角度等参数和主流雷诺数的影响。Ooi等[5]用v2-f、k-ε、S-A模型模拟了内部有横置肋片的直通道,发现v2-f模型的计算结果更接近实验数据,但不能很好地预测不带肋壁面的传热情况。Amano等[6]用k-ε、k-ω两种湍流模型,对静止条件下带扰流肋的涡轮冷却通道进行了数值计算,并与实验结果进行对比,发现k-ε模型的计算结果与实验数据较吻合。Slabaugh等[7]对设有单边扰流肋片的窄通道进行了数值研究,表明阻塞比增大,换热效果提高,但随之流动损失增大。
本文以扰流通道为原始模型,在定雷诺数下,利用CFX软件对不同斜置角度下的原始模型进行模拟,并将所得数据输入自行编写的MATLAB程序寻优,以研究定雷诺数下,斜置肋片角度与带肋直冷却通道整体换热效果和综合换热性能的相关情况。
2 模型与寻优
数值模拟使用以有限体积法和隐式方法求解三维稳态N-S方程组的CFX软件。求解过程中,选用二阶精度的差分格式,计算残差设定在10-5以下收敛。湍流模型选用k-ε模型和自动壁面函数处理方式。利用MATLAB程序运算,得出带肋壁面最大整体换热效果下的肋片斜置角度和综合换热性能最优时的肋片斜置角度。
2.1 几何模型与边界条件
几何模型以Han等[1]的带肋直冷却通道作为原始计算模型,见图1。该模型的通道横截面为正方形,其上下壁面分别设置有10个截面为方形的横置肋片,肋高e=2.38125 mm,肋高与当量直径D之比为0.047:1,肋高与肋间距P之比为1:10,直通道截面高H与肋宽W之比为1:1,雷诺数Re取定值10000。

图1 原始计算模型的结构Fig.1 The structure of the original model
为减少计算模型的整体网格数量以节省计算时间,提高重点关注区域的计算精度,根据CFX软件功能,对原始计算模型进行了改造,采用具有对称性的带肋直通道模型,如图2所示。

图2 改造后的计算模型结构Fig.2 Reconstructed calculation model
计算模型边界条件:进口设置为速度进口,给定Re=10000时相对应的法向速度,出口设置为静压101325 Pa,带肋壁面和两侧光滑壁面给定热流密度定值q,顶面设置为直通道对称面。
计算模型采用结构化六面体网格形式,在各肋之间的重点求解区域局部加密,其它部分与直通道计算模型的整体网格密度相同。求解模型带肋壁面的距壁面距离的无量纲值均小于2,满足模型计算要求。图3示出了内部斜置角度60°肋片的直冷却通道网格。
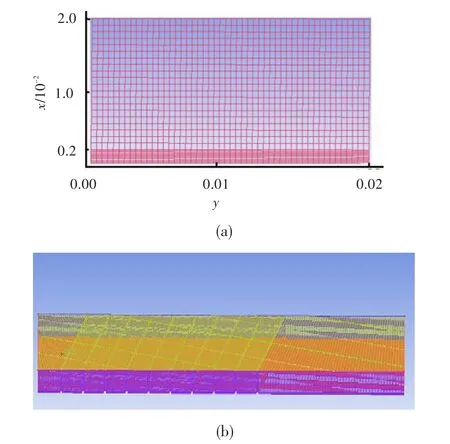
图3 斜置角度为60°的网格示意图Fig.3 Grid map of oblique angle of 60 degrees
2.2 寻优
2.2.1 不同斜置角度下的整体换热效果
衡量换热效果的好坏通常引用努赛尔数来表示。直冷却通道的换热系数h和努赛尔数Nu的定义分别为:

式中:λ为冷却空气的传热系数;TW为通道的壁面温度;Tf为参考温度,文中取进口冷却空气的平均温度为参考温度。
对直通道内部肋片的斜置角度从30°至60°以5°为等差,划分为7种工况,分别进行相同边界条件下的数值模拟,并以所得带肋壁面的平均努赛尔数和斜置角度输入MATLAB程序寻优。通过CFX后处理软件CFD-Post中的面积加权均值法求得。运算结果如图4所示,当α=48.62°时,----Nu=139.566,带肋壁面的----Nu最大,整体换热效果最好。
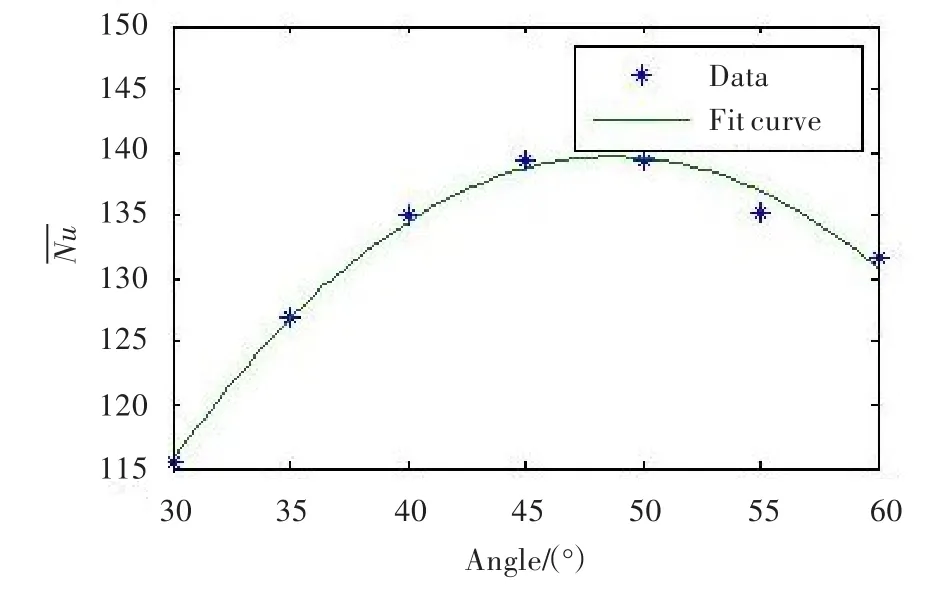
图4 斜置角度与带肋壁面平均努赛尔数的拟合曲线Fig.4 Fitted curve of α and----Nu
2.2.2 不同斜置角度下的综合换热性能

在直通道内部流动模拟过程中,以实际流动损失与完全湍流发展时光滑管道的流动损失之比来表示流动损失情况,有:

式中:Pin为进口压力,Pout为出口压力,L为直通道计算模型的长度,G为进口冷却空气的质量流量,Re=10000。
综合考虑换热效果和流动损失对直通道整体换热性能的影响,综合换热系数N的表达式为:

将综合换热系数与斜置角度代入程序进行拟合,结果见图 5。可见,当α=30.34°时,N=1.664,带肋直通道的综合换热性能最好。
3 计算与验证结果分析
3.1 湍流模型结果
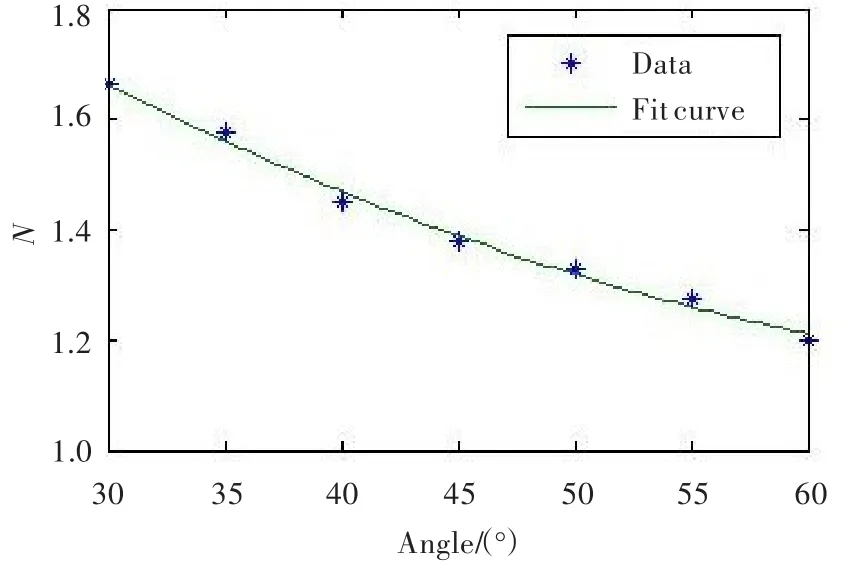
图5 斜置角度与综合换热系数的拟合曲线Fig.5 Fitted curve ofαandN
分别采用k-ε、k-ω和SST湍流模型,对直冷却通道的换热与流动特性进行数值模拟,并将其结果与Han等[1]的实验数据进行对比。由图6可看出,k-ω和SST湍流模型的模拟结果明显小于实验数据,其偏差过大;而k-ω湍流模型所得结果与实验数据吻合较好,能很好地(定性和定量)反映直冷却通道的整体换热效果。下文中模拟结果均采用k-ε湍流模型得到。

图6 不同湍流模型带肋壁面肋间努赛尔数与实验数据的对比Fig.6 Nuvs.experimental data of different turbulence model
3.2 不同斜置角度下的整体换热效果
对于通过MATLAB程序运算得出的结果,须经CFX软件进行同等条件下的数值模拟,以印证程序寻优结果。结果表明,当α=48.62°时,----Nu=139.562,其带肋壁面的----Nu与寻优结果的差值小于0.005,寻优结果可信度很高。
图7很好地展示了不同斜置角度下带肋壁面的换热效果。可见,α=48.62°时,----Nu最大,其换热效果明显比其它角度下的好,其肋顶端的高换热区域几乎全部被覆盖,肋间壁面的高换热区域影响也最大,覆盖面积也最广;α=90°时,整体换热效果最差。
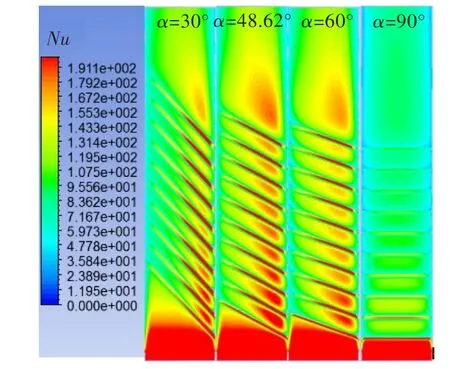
图7 不同斜置角度下带肋壁面的努赛尔数云图Fig.7 Nucontour of ribbed surface of differentα

图8 不同斜置角度下肋间壁面的努数比值Fig.8 grid figure of wall between the ribs of differentα
图8示出了不同斜置角度下肋间壁面的换热效果。可见,当α=48.62°时,肋间壁面的努数比最大,整体换热效果最好,并且沿冷却流体的总流动方向,各肋间壁面的换热效果相差不大,其平均换热效果更加理想;α为30°和60°时,各肋间的努数比差值较小,平均换热效果也较好,但努数比值均比α=48.62°时的低;α=90°时,肋间壁面的换热效果浮动较大,导致带肋壁面冷却不均现象比较严重。
3.3 不同斜置角度下的综合换热性能
对于带肋直冷却通道综合换热性能,需综合考虑直通道的流动损失和整体换热效果。
从图9中不同斜置角度下的流动损失可看出,30.34°斜置肋片产生的流动损失最小,45°和 90°斜置肋片引起的流动损失相差不大,60°斜置肋片导致的流动损失最大。
图10展示了不同斜置角度下的综合换热系数。可见,30.34°斜置肋片直冷却通道的综合换热性能最好,N=1.664;30°斜置肋片的综合换热性能(N=1.662)与 30.34°的基本相同,可认为 30°斜置肋片直冷却通道的综合换热性能最好;45°、60°斜置肋片的综合换热系数均比30°时的低。

图9 不同斜置角度下的流动损失Fig.9 Flow loss of differentα

图10 不同斜置角度下的综合换热系数Fig.10 Integrated heat transfer coefficient N of differentα
4 结论
(1)带肋直通道在定雷诺数下,肋片的斜置角度与整体的换热特性呈近似抛物线关系,综合换热性能与斜置角度呈近似对数关系。
(2)内设48.62°斜置肋片的直冷却通道换热能力最强,换热效果最佳,且冷却平均度较其它角度有更大的优势;90°横置肋片的换热效果最差。
(3)直冷却通道内设30°斜置肋片的结构产生的流动损失最小,其综合换热性能最好,且大大优于其它角度。
[1]Han J C,Park J S,Ibrahim Y M.Measurement of Heat Transfer and Pressure Drop in Rectangular Channels with Turbulence Promoters[R].NASA CR-4015,1986.
[2]Park J S,Han J C,Huang Y,et al.Heat Transfer Perfor⁃mance Comparisons of Five Different Rectangular Chan⁃nels with Parallel Angled Ribs[J].International Journal of Heat and Mass Transfer,1992,35(11):2891—2903.
[3]Hsieh S S,Hong Y J.Heat Transfer of Air Channel Flow over Repeated Ribs with Staggered Type Configuration[R].AIAA 89-0426,1989.
[4]Stephens M A,Shih T I P,Civinskas K C.Effects of In⁃clined Rounded RIBS on Flow and Heat Transfer in a Square Duct[R].AIAA 95-2115,1995.
[5]Ooi A,Iaccarino G,Durbin P A,et al.Reynolds Averaged Simulation of Flow and Heat Transfer in Ribbed Ducts[J].International Journal of Heat and Fluid Flow,2002,23(6):750—757.
[6]Amano R S,Guntur K,Lucci J M.Computational Study of Heat/Mass Transfer Characteristics in a Ribbed Cooling Channel in a Stationary Gas Turbine Blade[R].AIAA 2009-4520,2009.
[7]Slabaugh C D,Valentino M,Ricklick M,et al.Heat Trans⁃fer and Friction Augmentation in a Narrow Rectangular Ductwith Ribs Applied to One Wall[R].AIAA 2010-6952,2010.

