量子霍尔效应的研究及进展

张 琳，米斌周

(华北科技学院基础部，北京东燕郊 101601)

2013年，由清华大学、中国科学院物理所联合组成的研究团队首次从实验中观测到“量子反常霍尔效应”，这项重大基础物理学成果被诺贝尔物理奖获得者杨振宁称为“中国实验室里发表的第一次诺贝尔奖级的物理学论文。”此消息引起了国人的振奋与自豪，可是“量子反常霍尔效应”是怎样的效应?它与霍尔效应、量子霍尔效应有什么异同?它又可能会给人类的生活带来什么变化?相信很多人对此并不清楚，也不太理解为什么此发现发表的论文被杨振宁称为“中国实验室里发表的第一次诺贝尔奖级的物理学论文”?不妨回顾一下霍尔效应系列的发展史及其应用，相信上述一系列问题将得到解答。

1 霍尔效应

霍尔效应是指当电流垂直于外磁场通过导体时，在导体的垂直于磁场和电流方向的两个端面之间会出现电势差，这一现象就是霍尔效应。这个电势差也被称为霍尔电势差。如图1所示，将一块导电板中通以x方向的电流I，置于z方向的磁场B中，则在垂直于磁场和电流方向的两个面A、A'之间会产生霍尔电压UH。其中KH称为霍尔系数。如果撤去磁场，或者撤去电流，霍尔电压也就随之消失。

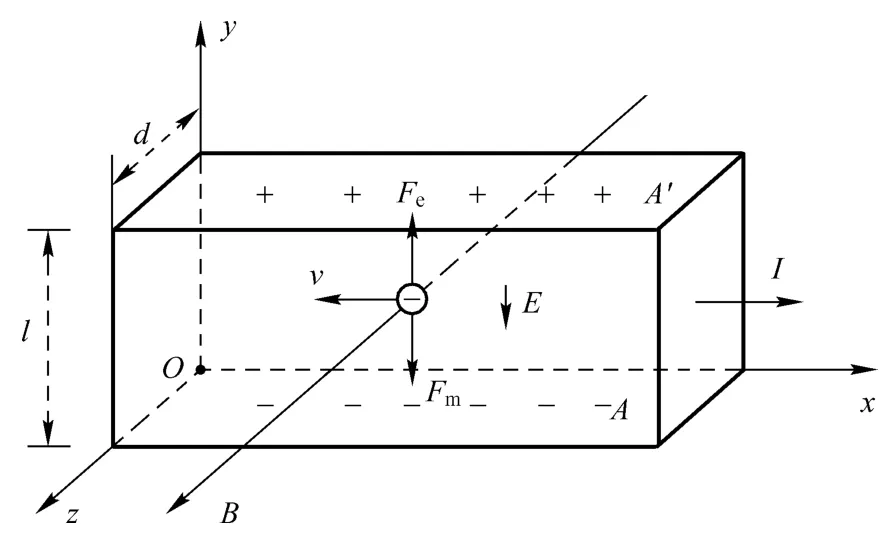
图1 霍尔效应示意图

霍尔效应可以用电荷在电磁场中的运动来解释［1－5］。电荷所受电场力等于洛伦兹力时，就达到了动态平衡。设导体板的载流子数密度为n，则电子平均漂移速度v与电流I的关系式为I=nevS=nevld，于是(1)式可改写为:

由(2)式可得霍尔电阻RH为:

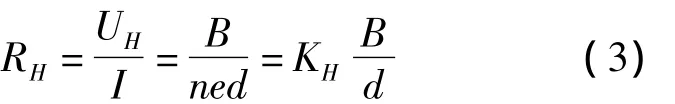
可见，在霍尔效应中，当霍尔材料确定时，霍尔电阻与外加磁场为线性关系。当然，材料的霍尔电阻率ρ=RHS/l=RHld/l=RHd也与外加磁场成线性关系。

上述讨论中载流子为电子，所得霍尔电压和霍尔系数均为负值。UH＞0为正电荷导电(P)型半导体，UH＜0为负电荷导电(N)型半导体。根据霍尔效应做成的霍尔器件，就是以磁场为工作媒体，将物体的运动参量转变为数字电压的形式输出，使之具备传感和开关的功能［2－5］。

2 反常霍尔效应

1880年，霍尔在研究磁性金属的霍尔效应时发现，材料的横向电阻率不再与磁场成正比，其关系如图2所示，此现象无法用简单的磁场洛伦兹力来解释，称此为反常霍尔效应［6，7］。

反常霍尔电导是由于材料本身的自发磁化而产生的，因此是一类新的重要物理效应。在反常霍尔效应中，由于材料本身的自发磁化，出现了通常大于常规霍尔效应系数R0一个量级的反常霍尔效应系数RS，其值强烈依赖于温度，且铁磁材料的霍尔电压值与外加磁场不再成线性关系;在铁磁材料中，即使不加外磁场，只通入x方向电流的情况下，仍能产生霍尔效应［6］。反常霍尔效应是探究和表征铁磁材料中巡游电子输运特性的重要手段和工具之一，它的测量技术被广泛应用于许多领域，最重要的应用是在新兴的自旋电子学方面，如稀磁半导体材料的诞生［8，9］以及以后对稀磁半导体材料应用的研究，反常霍尔效应必定还会肩负重任。

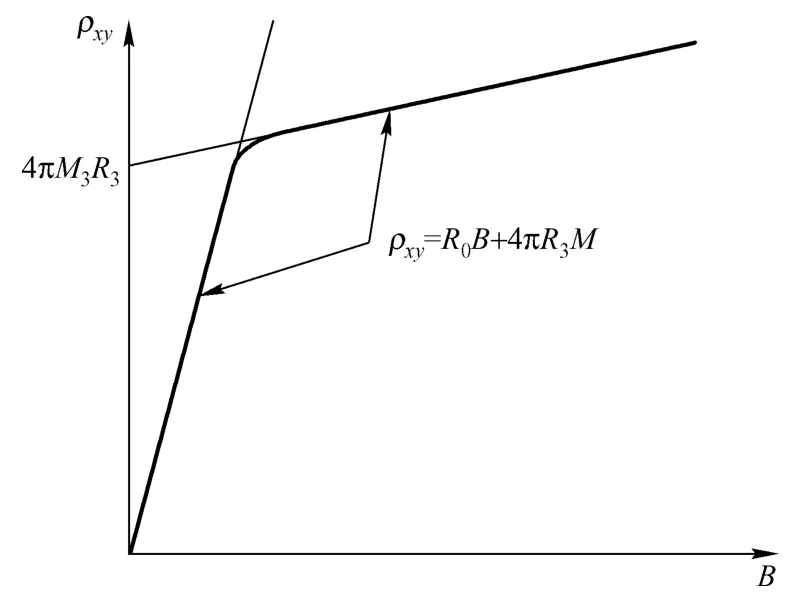
图2 霍尔电阻率ρxy与磁场大小的关系曲线示意图

3 量子霍尔效应

量子霍尔效应一般被看作是整数量子霍尔效应和分数量子霍尔效应的统称。作为微观电子世界的量子行为在宏观尺度上的完美体现，量子霍尔效应一直在凝聚态物理研究中占据着极其重要的地位。1980年，德国科学家冯·克利青发现整数量子霍尔效应，于1985年获得诺贝尔物理学奖。1982年，美籍华裔物理学家崔琦、美国物理学家施特默等发现了分数量子霍尔效应，这个效应不久由另一位美国物理学家劳弗林给出理论解释，三人共同分享了1998年诺贝尔物理奖［10］。

3.1 整数量子霍尔效应

德国物理学家冯·克利青等在二维电子系统:金属－氧化物－半导体场效应晶体管(MOSFET)中的反型层的霍尔效应实验中，得到一项意外发现［1，11－16］:在低温(约 1.5K)、强磁场(约 18万高斯)的条件下，发现了一个与经典霍尔效应完全不同的现象:霍尔电阻RH随磁场的变化出现了一系列量子化电阻平台，这种现象称为整数量子霍尔效应。这些平台电阻为:

式中h为普朗克常数，e为元电荷。图3［12］可以清楚地看到这些霍尔电阻平台。

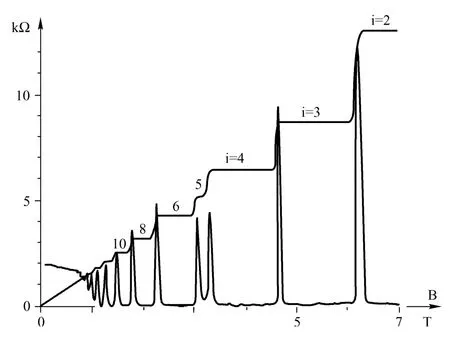
图3 整数量子霍尔效应

整数量子霍尔效应因其独有的特点有着重要的应用［2，11－16］。利用量子霍尔效应测得欧姆基准值，并于1988年电学咨询委员会第18届会议上正式提出将第一阶霍尔电阻平台的电阻定义为冯·克利青常数，符号为RK，精确的取值为RK=25 812.807 Ω，约定值 Rk－90，并规定此值从 1990年1月1日起，由所有以量子霍尔效应为电阻测量标准的实验室使用.这个新的电阻标准是以量子霍尔效应［14］为基础，既容易复现，又不会随时间变化.量子霍尔效应的另一个重要的应用就是高精度地测定了精细结构常数α.它是用来量度电磁相互作用强度的.精细结构的最初得名是指原子(特别是氢原子)和分子光谱中因电子自旋－轨道相互作用和转动振动等引起的谱线精细分裂.在SI单位制中，精细结构常数［15－17］的表达式为为光速，h为普朗克常数，e为电子电荷，μ0为真空磁导率，由量子霍尔效应测定的α的倒数，α－1=137.035 990 2(85)，不确定度为6.2×10－8，可以看出其很高的精确度［18］。

3.2 分数量子霍尔效应

1982年，崔琦、施特默等在对半导体砷化镓异质结(另一种二维电子系统)的霍尔效应实验研究中，在比整数量子霍尔效应更低的温度(约0.5 K)和更强的磁场(约20万高斯)的条件下，观测到在霍尔电阻RH与磁场磁感应强度B的关系曲线上，也在一些电阻和温度范围内观测到横向霍尔电阻呈现平台而同时纵向电阻减小到零的现象，但极为不同的是，这些平台对应的不是原来量子霍尔效应的整数值，而是分数值，故称为分数量子霍尔效应［11－14，19－20］(如图 4)。

图4 分数量子霍尔效应

正在人们对分数量子霍尔效应的出现解释不一时，1983年，美国物理学家劳克林提出了一种奇特的多粒子波函数，解释了一系列主要的实验事实，同时也让人们认识到可能存在一种新型的不可压缩的量子液体，这也开创了凝聚态物理强关联研究系统的一个新领域［11，20－21］。

4 自旋霍尔效应

最近几年，自旋霍尔效应(Spin Hall Effect，SHE)［22］引起人们的强烈兴趣，自2004年被美国加州大学圣巴巴拉分校Awschalom团队［23］首次在实验上观测到以来，已成为目前凝聚态物理中一个相当热门的研究方向.由于相对论效应自旋－轨道耦合作用的存在，人们发现在这样的体系中，在没有外加磁场条件下即使是在非磁性材料中，也存在类似的霍尔效应:自旋向上的电子和自旋向下的电子分别向两边运动从而分离开来.与以往跟电荷相关的霍尔效应完全不同，这种霍尔效应与电子的自旋密切相关.由于电子的自旋与电荷一样，可以用来储存和传递信息，而且自旋霍尔效应中的电流几乎没有能量损失，也就是说不会发热，因而引发了科学界对研制新的电子元器件的设想［24］.

随着SHE的研究发展，张首晟领导的研究团队提出的“量子自旋霍尔效应”(见图5)被《科学》杂志评为2007年“全球十大重要科学突破”之一［25］。因在“量子自旋霍尔效应”理论预言和实验观测领域的开创性贡献，张首晟与4位欧美科学家共同荣获2010年“欧洲物理奖”，他也是获得该奖项的首位华人科学家。

“量子自旋霍尔效应”找到了电子自转方向与电流方向之间的规律。利用这个规律可以使电子以新的姿势非常有序地“舞蹈”，从而使能量耗散很低。这种新奇的物理现象有可能给未来的信息革命带来重大影响，电脑甚至量子计算都将随之发生巨大改变。张首晟曾表示，“量子自旋霍尔效应”的理论研究以及产业化开发，对科学界和信息产业界来说，都将是一次大洗牌的机会。

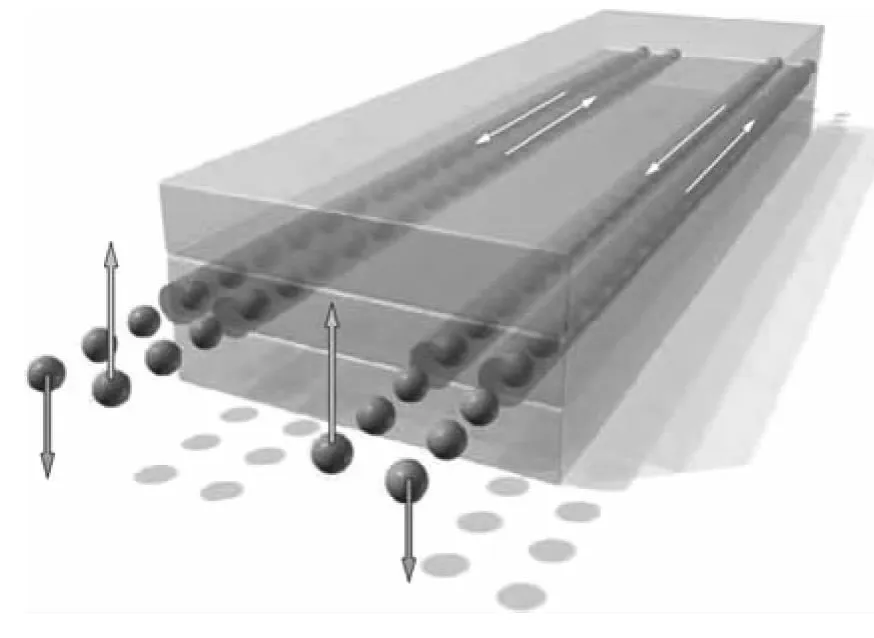
图5 量子自旋霍尔效应示意图

5 量子反常霍尔效应

量子反常霍尔效应不同于量子霍尔效应，它不依赖于强磁场而由材料本身的自发磁化产生。在零磁场中就可以实现量子霍尔态，更容易应用到人们日常所需的电子器件中。2013年，由清华大学薛其坤院士领衔、清华大学物理系和中科院物理研究所组成的实验团队从实验上首次观测到量子反常霍尔效应。美国《科学》杂志于2013年3月14日在线发表这一研究成果。

1988年，美国物理学家霍尔丹(F.Duncan M.Haldane)提出可能存在不需要外磁场的量子霍尔效应，理论上预计了纵向和横向电导率的测量结果，即在一定的条件下，电导率呈现量子化(见图6)。但是多年来一直未能找到能实现这一特殊量子效应的材料体系和具体物理途径。

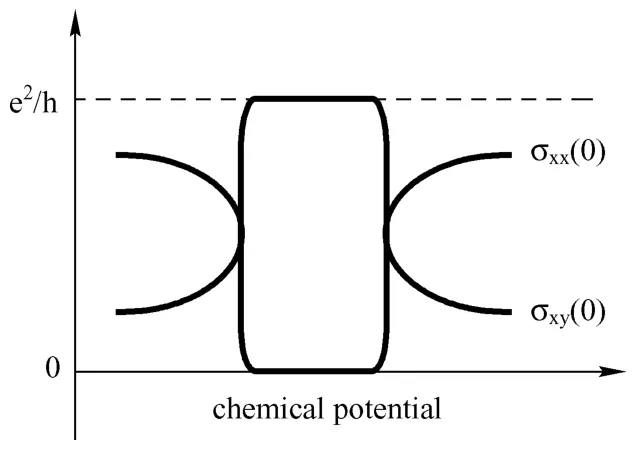
图6 量子反常霍尔效应的理讼预言

2010年，中科院物理所方忠、戴希带领的团队与张首晟教授等合作，从理论与材料设计上取得了突破，他们提出Cr或Fe磁性离子掺杂的Bi2Te3、Bi2Se3、Sb2Te3族拓扑绝缘体中存在着特殊的V.Vleck铁磁交换机制，能形成稳定的铁磁绝缘体，是实现量子反常霍尔效应的最佳体系。［26］

2013年3月，由清华大学薛其坤院士领衔，清华大学、中科院物理所和斯坦福大学研究人员联合组成的团队在量子反常霍尔效应研究中取得重大突破，他们克服了薄膜生长、磁性掺杂、门电压控制、低温输运测量等多道难关，一步一步实现了对拓扑绝缘体的电子结构、长程铁磁序以及能带拓扑结构的精密调控，利用分子束外延方法生长出了高质量的Cr掺杂(Bi，Sb)2Te3拓扑绝缘体磁性薄膜，并在极低温输运测量装置上成功地观测到了“量子反常霍尔效应”(见图7)。

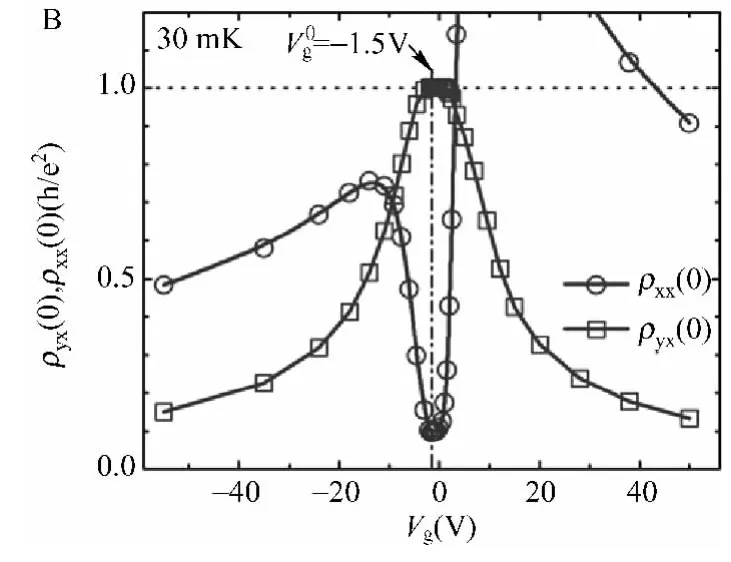
图7 在Cr掺杂的(Bi，Sb2)2Te3拓扑绝缘体磁性薄膜中测量到的霍尔电阻

量子反常霍尔效应的美妙之处是不需要任何外加磁场，因此，这项研究成果会推动新一代的低能耗晶体管和电子学器件的发展，可能加速推进信息技术进步的进程。

至此，量子霍尔效应家族的三成员量子霍尔效应，量子自旋霍尔效应，量子反常霍尔效应(见图8)均已面世，三种量子霍尔效应，电子都沿着无耗散的边缘运动，材料内部是绝缘的。他们的逐一面世，使人类利用其无耗散的边缘态发展新一代的低能耗晶体管和电子学器件更有可能，亦有可能解决电脑发热问题和摩尔定律的瓶颈问题，因此，量子霍尔效应家族三成员的面世将会推动新一代的低能耗晶体管和电子学器件的发展，可能加速推进信息技术革命的进程。

图8 量子霍尔效应，量子自旋霍尔效应，量子反常霍尔效应示意图

随着1880年霍尔效应的发现，至2013年量子反常霍尔效应的实验证实，霍尔效应家族成员已齐聚一堂，虽然量子霍尔效应等的应用还未能真正实现，但其发展潜能是毋庸置疑的，必在将来服务于人类的生产和生活.

［1］ 马文蔚.物理学中册第四版［M］.北京:高等教育出版社，2003:159－162.

［2］ 朱孟正，赵春然.浅论霍尔效应的发展及其应用［J］.牡丹江师范学院学报(自然科学版)，2012，(1):15－16.

［3］ 王本菊.霍尔效应及其应用［J］.中国校外教育下旬刊，2011，(6):76，107.

［4］ 程姝丹，张强.霍尔效应的应用与发展［J］.水泥技术，2007，(4):78 －82.

［5］ 张海涛.霍尔效应及应用［J］.温州职业技术学院学报，2005，5(4):26 －28，41.

［6］ 梁拥成，张英，郭万林，等.反常霍尔效应理论的研究进展［J］. 物理，2007，36(5):385 －390.

［7］ 杨锡震，杨道生，田强.异常霍尔效应和自旋霍尔效应［J］.物理实验，2005，25(10):3 －6.

［8］ Ohno H.，Munekata H.，Penney T.，et.al.Magnetotransport properties of p－type(In，Mn)As diluted magneticⅢ －Ⅴsemiconductors［J］.Phys.Rev.Lett.，1992，68:2664 －2667.

［9］ Ohno H.，Making nonmagnetic semiconductors ferromagnetic［J］.Science，1998，(281):951 －956.

［10］ 中国首次发现量子反常霍尔效应或引爆新革命［EB/OL］.中国网，2013－03－16.

［11］ 赖武彦.量子霍尔效应［J］.自然杂志，1985，8(1):16－20.

［12］ 聂素琴，陈泽章.霍尔效应的最新发展及应用［J］.科技资讯，2009，(2):229.

［13］ 张会云.霍尔效应的发展及应用［J］.纺织高校基础科学学报，2002，15(1):75 －79.

［14］ 杨锡震，田强.量子霍尔效应［J］.物理实验，2001，21(6):3－7.

［15］ 沙振舜.量子化霍尔效应研究进展［J］.低温与超导，1983，33(3):46 －53.

［16］ 章宏睿.量子霍尔效应及其在计量中的应用前景［J］.低温与超导，1983，32(4):44 －48.

［17］ 张郡亮，李运豹.精细结构常数及其物理意义［J］.大学物理，2008，27(6):24 －25.

［18］ 李国栋.无所不在的磁·诺贝尔奖百年鉴［M］.上海:上海科技教育出版社，2000:111－120.

［19］ 黄永南.量子霍尔效应简介［J］.固体电子学研究与进展，1986，6(3):220 －225.

［20］ 郭奕玲.1998年诺贝尔物理学奖—分数量子霍尔效应的发现［J］. 百科知识，1999，(1).

［21］ 虞跃.量子霍尔效应和诺贝尔物理学奖［J］.科学，1999，51(1):55－57.

［22］ 崔德怀.自旋霍尔效应现象的研究［J］.牡丹江大学学报，2009，18(1):110 －111.

［23］ Kato Y K，Myers R C，Gossard A C，et al.Observation of the spin hall effect in semiconductors.Science，2004，306:1910－1913.

［24］ Qi X L，Zhang S C.The quantum spin Hall effect and topological insulators.Physics Today，2010，63:33－38.

［25］ 发现量子自旋霍尔效应.新浪科技 http://www.sina.com.cn 2007－12－21.

［26］ Rui Yu，Wei Zhang，Hai－ Jun Zhang，Shou － Cheng Zhang，et.al.Quantized Anomalous Hall Effect in Magnetic Topological Insulators［J］.Science，2010，(329)，61 － 64.