高阶振型对建筑结构层间位移的影响1

郭 靖陈健云余 流

1） 中国建筑第六工程局有限公司，天津 300451

2） 大连理工大学工程抗震研究所，大连 116023

高阶振型对建筑结构层间位移的影响1

郭 靖1）陈健云2）余 流1）

1） 中国建筑第六工程局有限公司，天津 300451

2） 大连理工大学工程抗震研究所，大连 116023

建筑结构层间位移是抗震设计的研究重点。本文基于广义层间位移谱，分析高阶振型对结构最大层间位移角以及对结构层间位移沿无量纲高度分布的影响，并通过调整结构侧向刚度比，分析高阶振型对结构层间位移变形类型的影响。结果表明：随着结构固有周期的增加，仅取一阶振型进行分析将会显著低估结构的最大层间位移角，高阶振型的影响决不能忽视；从结构层间位移沿无量纲高度分布的角度分析，高阶振型将会显著增加结构中上部位的层间位移需要；高阶振型将增加长周期结构的剪切变形和中上部位的弯曲变形需求，但对中下部位弯曲变形的影响并不明显；针对长周期结构的设计和分析，除计算最大层间位移角外，建议考虑层间位移沿结构高度的分布情况。

层间位移谱 高阶振型 层间位移分布 高层建筑 抗震设计

引言

建筑结构在地震动作用下所产生的变形是导致结构损坏的直接原因，结构抗震评估和设计需要满足变形要求，基于变形的抗震设计已成为研究重点（Aydinoglu，2003；Karavasilis等，2006）。我国《建筑抗震设计规范（GB 50011-2010）》（中华人民共和国国家标准，2010）明确指出：采用振型分解反应谱法计算地震作用和地震力分布时，振型个数选取振型参与质量达到总质量90%所需的振型数。王克峰等（2005）在建立平面框架结构模型进行层间位移研究中提出，高阶振型将控制结构的层间位移，考虑高阶振型十分有必要。目前考虑高阶振型的计算方法并不少见（秦泗凤等，2008；刘海成等，2009；孙国华等，2007），但并没有考虑高阶振型对建筑结构层间位移沿高度分布影响的研究，同时针对高阶振型所引起的建筑结构位移类型问题的研究也很少。

国内外建筑抗震设计规范中均将层间位移角作为结构变形的重要参考指标进行抗震设计和安全评定（丰定国等，2003）。而层间位移谱可以简单、直接地计算出结构的最大层间位移角，具有实际应用价值。本文基于广义层间位移谱，分析了高阶振型对最大层间位移角以及层间位移沿无量纲高度分布的影响，指出仅考虑基本振型的局限性，同时将高层建筑简化为纯弯曲和纯剪切结构，用于分析高阶振型对结构层间位移变形类型的影响。

1 广义层间位移谱

层间位移角（Interstory Drift Ratio）定义为相邻两层位移之差与层高的比值，用于控制结构的侧向刚度（Algan，1988）。而层间位移谱表述结构基本周期与最大层间位移角之间的关系，能够直接计算结构的最大层间位移角，对建筑结构抗震设计具有重要的意义。

Iwan（1997）基于波动理论，将建筑结构简化为连续的剪切梁，提出了层间位移谱方法，但由于该方法基于波动理论，未在实际工程中广泛应用；随后，Chopra等（2001）进一步研究指出：Iwan（1997）的层间位移谱法可以通过取足够多的振型，采用振型分析法进行计算，该方法更容易应用于工程设计；然而Iwan（1997）和Chopra等（2001）的方法都是将建筑物简化视为连续的剪切梁，可以合理地计算忽略竖柱的轴向变形且梁刚度远大于柱刚度的体系，而对于梁柱刚度比不大而且具有斜撑或剪力墙的框架体系，所做简化将不再适合。

Miranda等（2006）基于Chopra等（2001）的研究，对层间位移谱法进行了改进，提出广义层间位移谱法，该方法将建筑视为弯曲梁和剪切梁的组合模型，此模型可以代表更多类型的建筑体系，从而进一步拓展了层间位移谱法的应用范围。国内对层间位移谱的研究和应用相对较少，杨迪雄等（2009）和Yang等（2010）根据广义层间位移谱法分析近断层脉冲型地震动作用下结构层间变形特性和机理，证明该方法具有良好的实用性和高效性。广义层间位移谱简化分析模型如图1所示。

从图1中可以看出，弯剪型悬臂梁由弯曲悬臂梁和剪切悬臂梁通过水平刚性连杆连结组合而成，假设质量和刚度均匀分布，同时考虑由弯曲和剪切引起的结构变形。

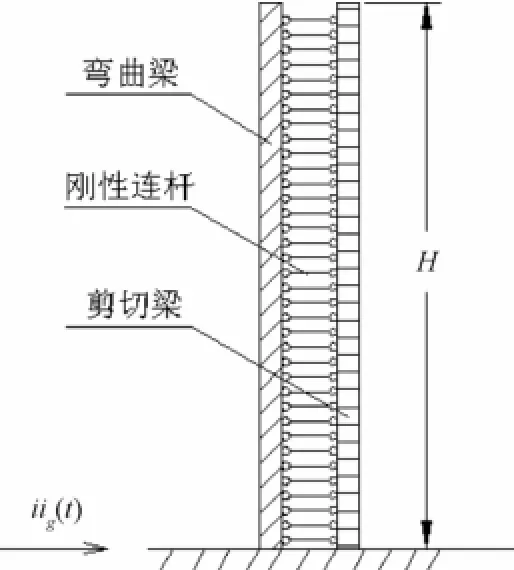
图1 弯剪型悬臂梁模型Fig. 1 Shear-flexural beam model used in generalized inter-story drift spectrum

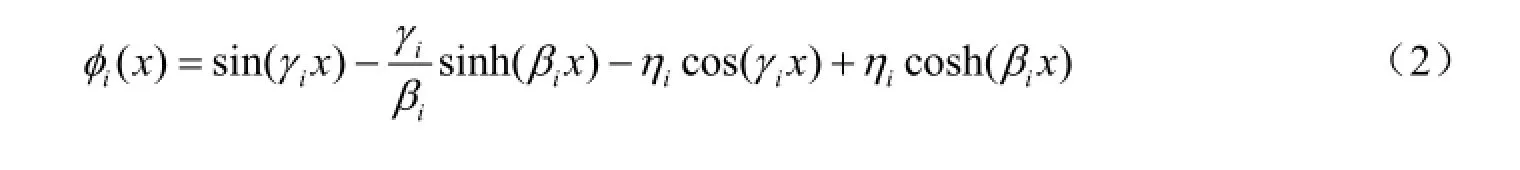
式中，iγ为第i阶振型的特征值，通过特征方程求出（Miranda等，2006）；iβ和iη为第i阶振型的无量纲参数，由下式求出：

假设弯剪梁模型是经典阻尼体系，则第i振型在t时刻，无量纲高度/xzH=处的侧向位移贡献表示如下：

式中，Γi为第i振型参与系数；φi(x)为第i振型在无量纲高度x处的振幅；Di(t)为周期为Ti、阻尼比为ξi的弹性单自由度体系在地面加速度u˙g(t)作用下的位移反应。

广义层间位移谱以振型分析为基础，体系的总位移可以通过振型叠加法计算求得：

无量纲高度x处的位移角可由位移(,)uxt对x求一阶导数求得：

其中，φi′(x)表示第i振型对x的一阶导数。

在已知结构的基本周期T1的情况下，高阶自振周期可通过下式求得：

各阶振型的参与系数可用下式计算：

在广义层间位移谱法中，利用结构第j层中部的转角估计本层的层间位移角，如下式所示：

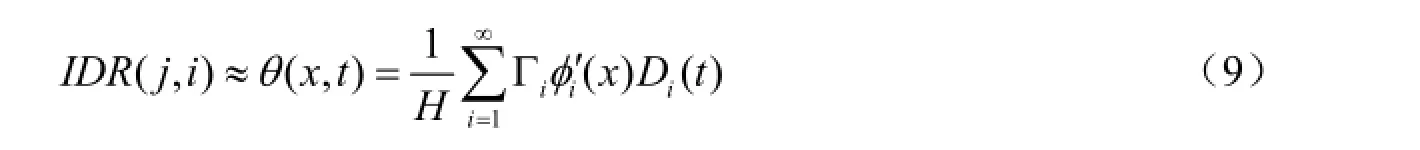
式中，x为第j层和第j+1层层高的平均值。

由（9）式可以看出，计算层间位移角需要计算模型的所有振型，Miranda等（2005）的研究表明，在大多数情况下，只需要提取前几阶振型就已经能够满足精度要求。因此，（9）式可简化为：

式中，m为计算所提取的振型数。综上所述，针对不同固有周期的结构，最大层间位移角为：

2 高阶振型对层间位移的影响

2.1 分析模型

本文在分析时根据现有研究成果（Miranda等，2006；杨迪雄等，2009），选取弯剪梁刚度比α=20表示弯剪框架结构（Miranda等，2002），假设阻尼比ξi=0.05，取振型阶数m=1，2，4，6；选用EL centro波和Kobe波做为地震动u˙g(t)输入，加速度峰值为0.3g，时程如图2所示。

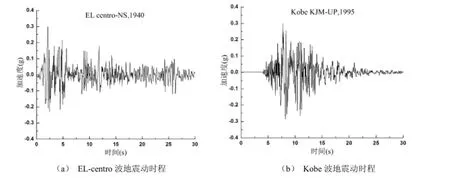
图2 地震动时程Fig. 2 Input ground motions

2.2 结果分析

选取不同振型数m的层间位移谱计算结果如图3所示。从图3中可以看出，随着周期的增大，仅取一阶振型计算的误差十分明显，将会显著低估结构的最大层间位移角，高阶振型的影响不能被忽略。同时还可以看出，在整个计算周期内，取结构的前4阶振型和前6阶振型进行计算，所得结果相差并不明显，表明超高阶振型影响并不大，甚至可以忽略不计。

在结构分析和计算过程中，不仅需要考虑最大层间位移角，同时分析层间位移的分布情况对结构优化设计以及防灾减灾同样具有实际意义。本文根据图3，选取较长固有周期T=4.0s作为算例，分析高阶振型对层间位移角沿结构无量纲高度分布的影响，如图4所示。当仅考虑一阶振型时，弯剪结构的层间位移沿高度的分布规律为中下部略大，而向上部逐渐减小；当考虑高阶振型时，结构中上部位的层间位移显著增加。结合图3（a）和图4（a）可知，当T=4.0s，仅考虑一阶振型的最大层间位移角与高阶振型所得结果误差并不十分明显，但是仅考虑一阶振型将会显著低估结构中上部的层间位移需求，这一点在层间位移谱中并不能体现；当层间位移谱计算结果差距较大时，如图3（b）和4（b）所示，结构中上部的层间位移需求将显著增加。因此，针对长周期结构，除计算最大层间位移角外，还需要考虑高阶振型对层间位移沿结构高度分布的影响。

图3 广义层间位移谱计算结果Fig. 3 Calculated results of generalized inter-story drift spectrum

图4 结构层间位移角沿无量纲高度分布图Fig. 4 Inter-story drift ratio distribution along dimensionless height

3 高阶振型对不同层间位移变形类型的影响

由图4可以看出，高阶振型对长周期结构层间位移分布的影响十分显著。弯剪型结构模型的位移由弯曲和剪切两种变形共同作用产生，本文进一步将建筑结构等效简化为纯弯曲结构和纯剪切结构，分析高阶振型分别对弯曲和剪切两种类型变形的影响。

计算所选参数和工况同第2节，根据广义层间位移谱推导原理（Miranda等，2002），分别取α=0和α=650表示纯弯曲结构和纯剪切结构。

纯弯曲结构的层间位移分布如图5所示。纯弯曲结构的层间位移变形表现为顶部最大，向结构底部逐渐减小。考虑高阶振型时，结构中上部的层间位移将会显著地增加，而对中下部位移的增加并不明显，如图5（b），当无量纲高度z/H＜0.5时，所选取的四种振型所得结果误差很小；而对图5（a），即使在下部有位移凸变，但是变化幅度与结构上部相比相对很小。可以看出，考虑高阶振型对于结构中下部的弯曲变形位移需求的影响并不明显。

图5 弯曲结构层间位移分布Fig. 5 Inter-story drift ratio distribution of flexural system

如图6所示，剪切结构的层间变形与弯曲结构相反，表现在底部最大，向结构顶部逐渐变小。考虑高阶振型时，不仅结构底部的位移需求明显增加，同时结构中上部的剪切位移需要增加幅度更为明显。图6（b）中上部的层间位移增加最为显著，与底部最大层间位移相比已相差不大。

图6 剪切结构层间位移分布Fig. 6 Inter-story drift ratio distribution of shear system

结合图5—6可知，对于长周期建筑结构，考虑高阶振型时，结构中上部的剪切和弯曲位移需求都将显著增大，进而出现图4所示层间位移分布的情况；但是对于结构中下部，考虑高阶振型只会显著增加该部位剪切变形位移需求，而对弯曲变形位移需求的影响并不明显。

4 结论

本文采用广义层间位移谱，分析高阶振型对最大层间位移角和层间位移分布的影响，同时分析了高阶振型对结构的弯曲和剪切变形的影响，所得结论如下：

（1）广义层间位移谱可以方便地计算结构的最大层间位移角，同时可以分析结构层间位移沿无量纲高度的分布情况，具有良好的应用和研究价值。

（2）分析广义层间位移谱可知，随着周期的增大，仅取一阶振型计算的误差十分明显，将会显著低估结构的最大层间位移角，高阶振型的影响不能被忽略。

（3）从层间位移分布的角度考虑，高阶振型将会显著增加结构中上部的位移需要；计算和分析长周期结构时，不仅需要考虑最大层间位移角，还应当考虑层间位移的分布情况。

（4）针对长周期建筑结构，高阶振型将会增加整体结构的剪切变形位移需要，而对结构下部的弯曲变形位移需求的影响并不明显。

致谢：衷心感谢大连理工大学工业装备结构分析国家重点实验室杨迪雄教授在对广义层间位移谱理论学习和程序编制的热心指导和帮助。

丰定国，王社良著，2003．抗震结构设计（第二版）．湖北：武汉理工大学出版社．

刘海成，郭全全，2009．考虑高阶振型影响的简化PUSHOVER分析方法．哈尔滨工业大学学报，41（10）：188—192．

秦泗凤，刘春光，林皋等，2008．基于改进ASPA法的高阶振型对桥墩抗震性能的影响评价．中国公路学报，21（5）：57—62．

孙国华，何若全，高晓莹，2007．Push-over方法中一种考虑高阶振型影响的水平荷载分布模型．北京工业大学学报，33（6）：587—591．

王克峰，周云，2005．考虑高振型影响的结构层间位移谱能力分析方法．地震工程与工程振动，（25）：33—40．

杨迪雄，潘建伟，李刚，2009．近断层脉冲型地震动作用下建筑结构的层间变形分布特征和机理分析．建筑结构学报，30（4）：108—118．

中华人民共和国国家标准，2010．建筑抗震设计规范（GB 50011-2010）．北京：中国建筑工业出版社．

Algan B.B.，1988．Drift and damage consideration in earthquake resistant design of reinforced concrete buildings．University of Illinois，Urbana-Champaign．

Aydinoglu M.N.，2003．An incremental response spectrum analysis procedure based on inelastic spectral displacements for multi-mode seismic performance evaluation ．Bulletin of Earthquake Engineering，（1）：3—36．

Chopra A.K.，Chintanapakdee C.，2001．Drift spectrum versus modal analysis of structure response to near-fault ground motions．Earthquake Spectra，17（2）：221—234．

Yang D.X.，Pan J.W.，Li G.，2010．Interstory drift ratio of building structures subjected to near-fault ground motions based on generalized drift spectral analysis．Soil Dynamics and Earthquake Engineering，30：1182—1197．

Iwan W.D.，1997．Drift spectrum：Measure of demand for earthquake ground motions．Journal of Structural Engineering，123（4）：397—404．

Karavasilis T.L.，Bazeos N.，Beskos D.E.，2006．Maximum displacement profiles for the performance based seismicdesign of plane steel moment resisting frames．Engineering Structure，28（1）：9—22．

Miranda E.，Rsyes C.J.，2002．Approximate lateral drift demands in multistory buildings with nonuniform stiffness．Journal of Structure Engineering，128（7）：840—849．

Miranda E.，Taghavi S.，2005．Approximate floor acceleration demands in multistory building I：Formulation．Journal of Structural Engineering，131（2）：203—211．

Miranda E.，Akkar S.D.，2006．Generalized interstory drift spectrum．Journal of Structural Engineering，132（6）：840—852．

Influence of Higher Modes on Inter-Story Drift of Multistory Buildings

Guo Jing1），Chen Jianjun2）and Yu Liu1）

1）China Construction Sixth Engineering Division Corp．LTD，Tianjin 300451，China
2）Institute of Earthquake Engineering，Dalian University of Technology，Dalian 116023，China

Inter-story drift ratio is the research emphasis of seismic design on multistory buildings．Based on generalized inter-story drift spectrum，the influence of higher mode on maximum inter-story drift ratio is analyzed．In the meantime，the influence on the deformation types is investigated by adjusting the lateral stiffness ratio．It is illustrated in this paper that with the increase of fundamental period of structure，the maximum inter-story drift ratio will be underestimated seriously if the fundamental vibration mode is just considered，and the influence of higher modes cannot be ignored; the deformation demands of the upper part will be increased obviously in the analysis of inter-story drift demands distribution．Furthermore，for the buildings with long fundamental period，the flexural deformation of the upper part and shear deformation increase significantly if higher modes are considered．More attention should also be paid that，for long-period structures，the inter-story drift demand distribution should be considered as well as the inter-story drift ratio．

Inter-story drift spectrum；Higher modes influence；Inter-story drift demand distribution; Multistory buildings；Seismic design

郭靖，陈健云，余流，2014．高阶振型对建筑结构层间位移的影响．震灾防御技术，9（4）：907—914．

10.11899/zzfy20140419

国家自然科学基金资助项目 (50978043)

2014-06-12

郭靖，男，生于1983年。博士，工程师。主要从事结构抗震研究。E-mail: guojing124@163.com