HDI板盲埋孔填胶量化分析及模型探索

魏 峥 史宏宇 李艳国 罗 娜（广州兴森快捷电路科技有限公司，广东 广州 510063）

HDI板盲埋孔填胶量化分析及模型探索

Paper Code: S-061

魏 峥 史宏宇 李艳国 罗 娜
（广州兴森快捷电路科技有限公司，广东 广州 510063）

文章定量分析了半固化片对盲埋孔填胶的影响因素，在此基础上，正交分析确定了盲埋孔填胶的主要控制因素（填胶深度和PP片数量），为前端工程设计和控制提供依据。最后，建立盲埋孔填胶的胶体流动模型，即在层流状态下的渗流模型，服从达西定律。

半固化片；胶体；渗流；达西定律

1 前言

为适应当今电子产品多功能化和微型化的发展需求，高阶HDI板逐渐成为PCB市场的主流产品。为保证产品盲埋孔的可靠性，业界主要采用两种树脂填充方法：一种是树脂塞孔工艺，另一种是直接利用半固化片的树脂填孔。两者相比较，后者明显具有流程短、成本低等优点，是一种优异的加工技术流程[1]。

但半固化片填胶工艺研究仍不完善，难点之一是影响因素众多[2]，其交互影响非常复杂，同时，采用量化分析方法无法对胶体的流动性进行分析。所以，定量分析半固化片对盲埋孔填胶具有局限性，未考虑胶的流动性、黏度及层压时胶体受到的压力，从而不能区分S1141、IT180等半固化片在胶含量一致时的流胶状态。

目前，行业内对半固化片填胶仍停留在量化分析的基础上，至今仍无人研究胶体流动规律，建立胶体流动模型对盲埋孔填胶进行研究。据此，本文定量分析了半固化片对盲埋孔填胶的影响因素，并建立了流体渗流模型对胶体流动进行分析，从胶体流动本质上分析盲埋孔填胶的规律，为填胶不良分析提供理论依据。

2 盲埋孔填胶量化分析

2.1 量化分析填胶影响

半固化片填胶定量分析满足总胶量守恒定律，即半固化片的总胶量不会凭空增加或减少，只能等量转移至盲埋孔及线路间距内。所以，半固化片的总胶量应满足盲埋孔及线路间距内的填充，即满足式（

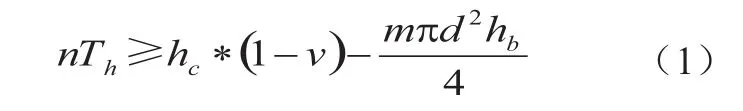
其中，n为半固化片片数量，Th为理论胶厚（表1），hc为铜厚，v为残铜率，hb为盲埋孔深度，d为孔径，m为孔数。

公式（1）表明：

（1）半固化片的总胶量nTh是由半固化片类型、数量两因素决定（如表1所示）；

（2）通常，半固化片需对盲埋孔及线路间距两处进行填胶，当填充线路间距时，影响因素由铜厚、残铜率决定；

（3）半固化片对盲埋孔进行填胶时，影响因素包括盲埋孔深度、孔径、孔数三者决定。

综上，半固化片填胶按照量化分析，含有7个影响因素，分别为半固化片类型、数量、铜厚、残铜率、盲埋孔深度、孔径、孔数。同时，由于影响因子众多，且影响规律和权重大小各不一致，所以，需确定重要影响因子，从而对关键因子进行重点控制或者条件限定，以下是采用正交方差的方法分析各因子的影响规律。

2.2 量化分析结果

表2为正交分析各因子的影响规律结果，将PP数量、盲埋孔深度、总孔数、残铜率合并在一起进行正交实验，分析计算各个因素影响权重大小。如表2所示，正交实设计是L9(34)，即4个因子，3个水平，根据田口实验设计方法选择了9组实验，重复试验3次，总共有27个实验。

根据以上正交分析结果进行误差分析，如下所示。

表3是对正交实验结果进行方差分析，可得到以下结论。

各因子A、B、C、D的F值均大于Fa（p-1，n-p）=3.55，所以，盲埋孔深度、半固化片数量、总孔数、残铜率均对填胶影响显著。

表1 常用半固化片的理论单面胶厚

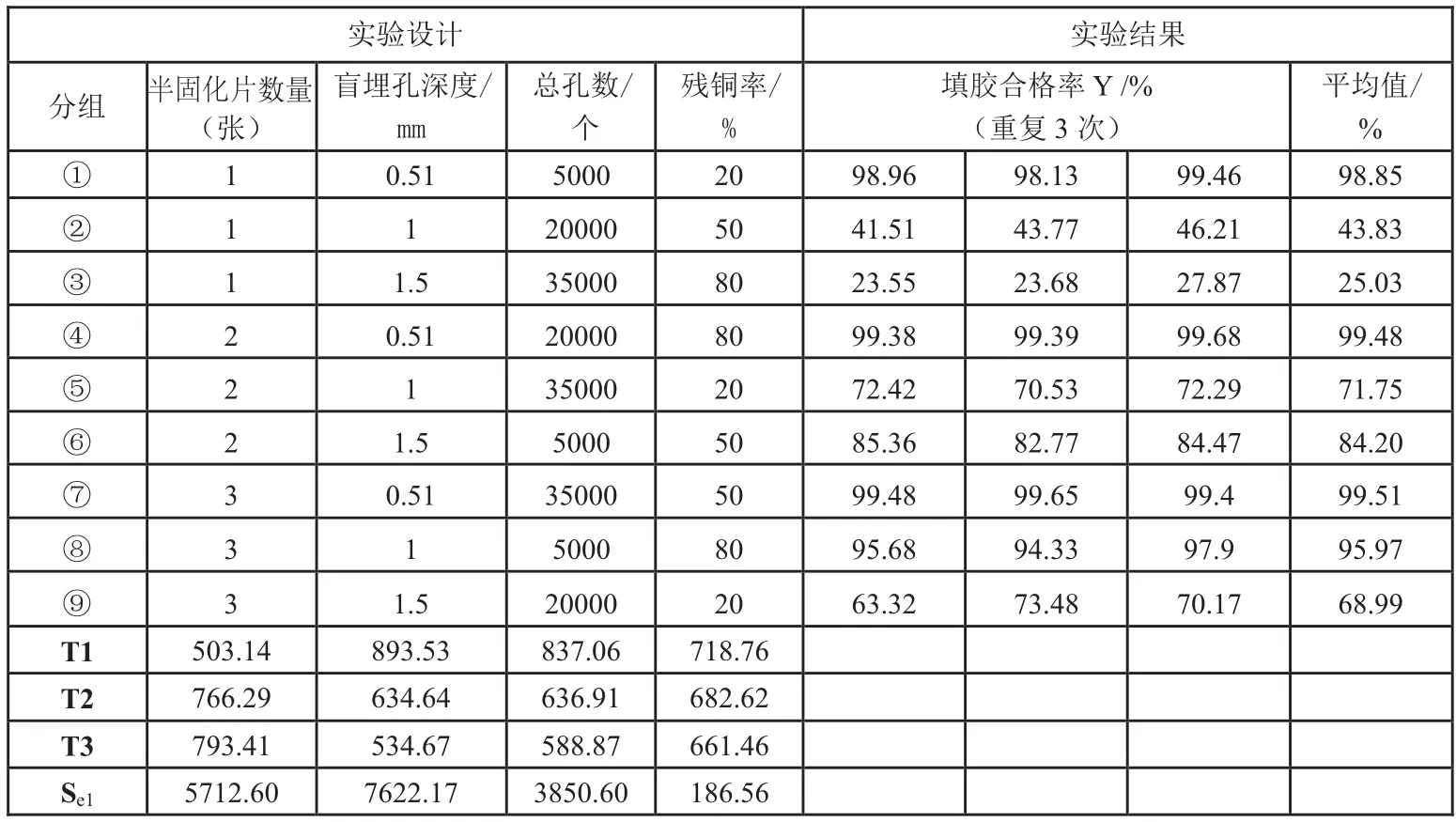
表2 正交实验结果

各因素影响程度可从贡献率表现，因子B最重要，它的水平变化引起的数据波动在总的平方和中占了43.88%；因子A，C贡献率其次；而因子D贡献率最小，仅占1.07%。

综上所述，盲埋孔深度、半固化片数量、总孔数、残铜率均对盲埋孔填胶均影响显著，其权重大小及分配情况为：盲埋孔深度（43.88%）＞半固化片数量（32.88%）＞总孔数（22.17%）＞残铜率（1.07%）。所以，量化分析表明，盲埋孔填胶的主要控制因素是盲埋孔深度和半固化片数量。

3 流胶模型探讨

由于量化分析半固化片对盲埋孔填胶具有局限性，未考虑胶的流动性、粘度、胶体受到的压力及流动时间，从而不能区分S1141、IT180等半固化片在胶含量相等时的填胶差异。所以，以下模型主要对胶体流动进行分析，并确定以上因素对盲埋孔填胶的影响规律。

3.1 模型建立

1883年Reynold（雷诺）发现：胶体流动分为两种状态，分别是层流状态和紊流状态。雷诺数是判定流体流动状态的重要依据。当Re≤2000时，流动状态为层流；当Re＞2000时，流动状态为紊流。

式中 ：Re为雷诺数（无量纲），为密度 ，d为盲埋孔直径，V为盲埋孔截面上的平均流速，为粘度（Pa·S）。

雷诺数如公式2所示，可知雷诺数是惯性力与黏性力的比值。雷诺数的大小表示了流体在流动过程中惯性力和黏性力的主导作用。雷诺数小（Re ≤2000），表示黏性力起主导作用，流体质点受黏性的约束，处于层流状态；而雷诺数大（Re＞2000），表示惯性力起主导作用，黏性不足以约束流体质点的紊乱运动，流动便处于紊流状态。

图1是胶体流动沿程阻力系数和雷诺数之间关系。如图所示，流体流动分为3个区：I层流区(服从达西定律)、Ⅱ过渡区和Ⅲ紊流区。其模拟结果同葛家理等人[3]的渗流实验结果在规律上是一致的。通过比较可以得出结论，在盲埋孔填胶的模拟中，胶体流动模型同渗流模型是等效的。

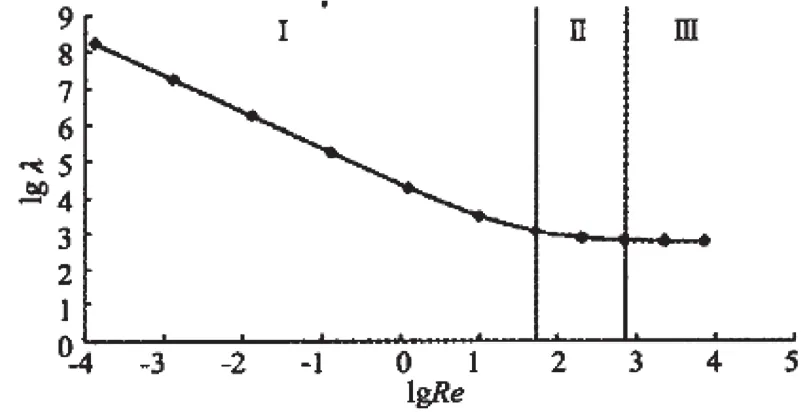
图1 胶体流动沿程阻力系数和雷诺数之间关系

所以，在层流状态下，盲埋孔的流胶模型同渗流模型是统一的。沿程阻力是一个宏观统计值，反映了流体能量损失变化对胶体流动的影响，流体在盲埋孔中流动时，由于流体与孔壁之间有粘附作用，以及流体质点与流体质点之间存在着内摩擦力等，沿流程阻碍着流体运动的阻力称为沿程阻力。为克服沿程阻力而损耗的机械能称为沿程能量损失，单位重量流体的沿程能量损失称为沿程能头损失，以hλ表示。

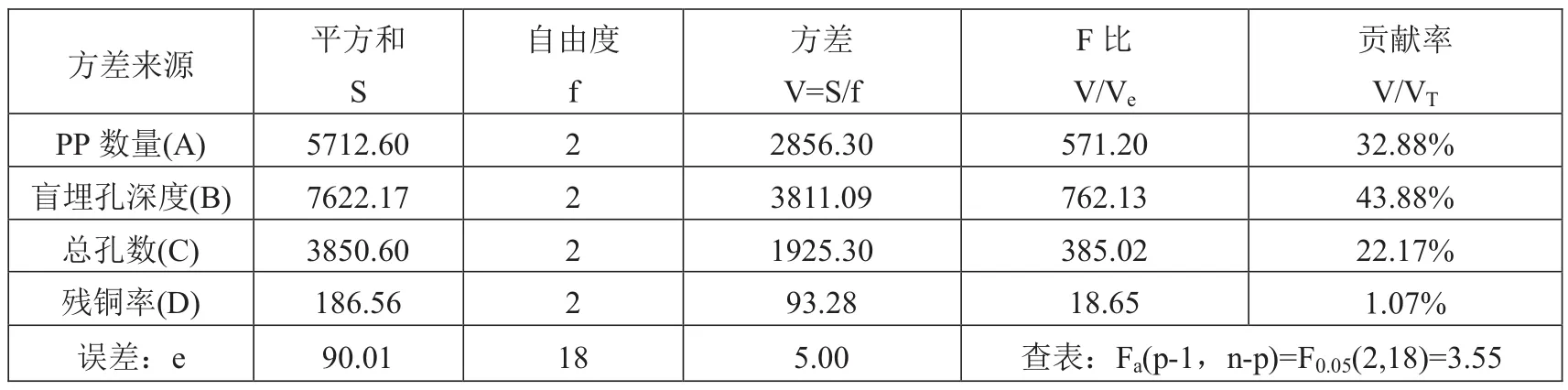
表3 方差分析

式中 ：λ是沿程阻力系数(无量纲) ，L是盲埋孔深度 ，d是盲埋孔直径，v为盲埋孔截面上胶的平均流速。

公式（4）表明，当盲埋孔内胶体流动处于层流状态时，流体流动速度同压力梯度成正比，这与达西定律一致，所以，可以用达西定律描述盲埋孔内胶体流动[4]。

综上所述，建立胶体流动模型分析盲埋孔填胶，即在层流状态下，盲埋孔的流胶模型同渗流模型是统一的，并且服从达西定律。

3.2 填胶模型应用

在层流状态下，盲埋孔的流胶模型服从达西定律，以下采用层流时的运动微分方程（牛顿力学分析法）计算盲埋孔内胶体流量，胶体的流量可反应盲埋孔内填胶趋势。

根据牛顿粘性定律，公式5是盲埋孔内速度分布，示意图如图3所示。

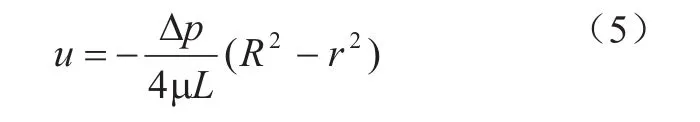
式中 ：是流体速度，是流体黏度，R是盲埋孔半径，L是盲埋孔深度 ，是压力梯度。

图3 盲埋孔内层流的速度和剪应力分布

在流过盲埋孔断面的任一半径r处，取一宽度为dr的圆环，如图4所示。因dr很小，可以认为其上速度相等，于是通过微元面积dA = 2πrdr上的微小流量[5]。

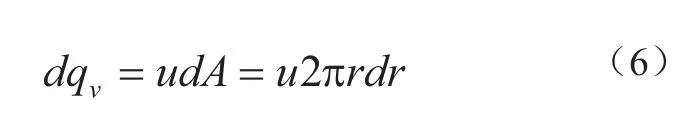
通过盲埋孔填胶的流量为：

式中 ：Q是盲埋孔填胶体积，qv是盲埋孔填胶的流量，u是胶体流动速度，R是盲埋孔半径，L是盲埋孔深度，为层压压力，为胶体流动时间。

公式8可知盲埋孔填胶体积与孔径、深度、胶体粘度、层压压力、胶体流动时间有关，具体表现为：

（1）盲埋孔填胶体积与孔半径大小R4成正比；

（2）盲埋孔填胶体积与填孔深度、胶体粘度成反比，即填孔深度越小，黏度越小，填胶量越大；

（3）盲埋孔填胶体积与压力、胶体流动时间成正比，即层压的压力、胶体流动时间对填胶有重要影响。

4 结论

采用量化分析和胶体流动模型，研究半固化片片对盲埋孔填胶规律，得出以下结论：

（1）量化分析盲埋孔填胶表明，影响因素包含半固化片、铜厚、残铜率、盲埋孔深度、孔径、孔数。其中，流胶深度和半固化片数量是盲埋孔填胶的主要影响因素，为前端工程设计及控制提供了依据。

（2）盲埋孔填胶的胶体流动和渗流模型在本质上是统一的。并且，在层流状态下，胶体流动模型服从达西定律，它为渗流模型模拟盲埋孔填胶问题提供了理论依据。

（3）盲埋孔填胶总体积与孔径R4、层压压力、胶体流动时间成正比，与胶体黏度、盲埋孔深度L成反比。

[1] 林灿荣,李艳国. HDI板埋孔填胶工艺研究[J]. 印制电路信息, 2012(4).

[2] 陈壹华. HDI填胶工艺的研究[J]. 印制电路信息, 2005 (2).

[3] 葛家理, 宁正福. 现代油藏渗流力学原理[M]. 北京:石油工业出版社, 2001.

[4] 郑松青, 志峰, 鲍敬伟. 基于数字模型的缝洞型油藏流体流动模型研究[J]. 长江科学院院报, 2009 (26).

[5] 柯葵, 朱立明. 流体力学与流体机械[M]. 上海: 同济大学出版社, 2009.

魏峥，硕士，现为技术中心研发工程师。

Research on analyzing quantitatively and filling model of HDI blind buried hole

WEI Zheng SHI Hong-yu LI Yan-guo LUO Na

The factors which affect the filling Blind-via/Buried-via with prepreg were analyzed quantitatively by orthogonal analytical methods in this article, then, the key ones (the depth of filling and the number of prepreg ) were concluded to provide the theoretical basis for the engineering design. Subsequently, the theoretical model of colloidal flow in filling Blind-via/Buried-via with prepreg was established by using seepage under the laminar flow relative to Darcy's law.

Prepreg; Colloid; Seepage; Darcy's Law

TN41

A

1009-0096（2014）04-0186-04