路基刚度不均匀对无砟轨道动力特性影响研究

张家玲，徐光辉，蔡 英

(西南交通大学土木工程学院，四川成都 610031)

路基结构的刚度不均匀对无砟轨道结构的动力特性影响很大，甚至危及行车安全。但如果对路基结构的刚度均匀性提出过高要求，又会增加施工碾压遍数，提高工程造价。为此，国内外学者对路基结构的刚度不均匀性进行了相关研究，这些研究一般采用不同波长、不同幅值的沉降曲线来模拟路基结构的不均匀。由于路基结构的不均匀沉降实质是路基结构的刚度不均匀引起的，当路基结构的刚度存在不均匀时，在荷载作用下，将产生不均匀沉降，这会导致轮轨动位移和动应力的增大，进而危及列车运行安全。

为了分析路基结构刚度不均匀对上部轨道结构动力特性的影响，建立无砟轨道—路基三维多层体系动力学模型。通过施加列车动荷载，分析路基结构各种刚度不均匀性状对轨道结构动力特性的影响，以此提出路基结构刚度不均匀的限值标准，指导路基结构施工质量的检验和控制。

1 无砟轨道—路基的多层体系模型

根据京沪高铁无砟轨道综合试验段路基的典型断面，利用非线性有限元软件ABAQUS，建立基于CRTSⅡ型板式无砟轨道—路基的多层体系模型。模型纵向长度按标准轨道板长度6 450 mm设置，模型组成为:①轨道板宽度为2 550 mm，厚度为200 mm;②砂浆调整层设计厚度为30 mm;③底座宽度为2 950 mm，厚度为300 mm;④级配碎石层顶宽为9 500 mm，厚度为400 mm;⑤基床底层采用 AB组填料，厚度为2 300 mm，路堤边坡为1∶1.5。模型建立了轨道板、CA砂浆层、底座板、路基4个部件，其中路基部件再剖分为级配碎石层和基床底层。模型的边界约束条件为:地基横向边界设置X向约束，底部设置X，Y和Z向约束，模型纵向前后2个断面设置Z约束。模型先施加自重应力，然后在轨道板的承轨槽位置施加列车动荷载。计算过程中，轨道板与CA砂浆的接触面允许产生分离，CA砂浆与底座板的接触面不产生分离，底座板与级配碎石的接触面允许产生分离，路基内部各层间的接触面不允许产生分离。

2 模型荷载及计算参数

2.1 模型荷载

1)自重荷载:由于自重荷载对模型层间的接触状态有较大影响，因此在建立模型时需要考虑自重荷载对模型系统的动力影响。

2)列车荷载:由于钢轨具有弹性，一个车轮的荷载往往由几根轨枕来承担，同理，在某根轨枕上，可能要承担多个轮载的作用，为了准确考虑承轨槽所承担的荷载，对承轨槽上的荷载按群轮作用考虑，即

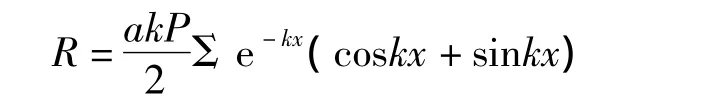
式中:R为作用在承轨槽上的压力;a为承轨槽间距;k为刚比系数;P为轮载;x为轮载作用点与承轨槽之间的水平距离，可以用列车运行的速度和时间表示。Σ e－kx(coskx+sinkx)为转向架车轮荷载沿纵向分布系数。

2.2 模型计算参数

无砟轨道—路基多层体系模型的主要参数见表1。级配碎石层正常模量值取为190 MPa，其他值为模拟刚度不均匀部位的模量值;为了模拟基床底层对轨道结构动力性能的影响，AB组填料正常模量值为120 MPa，其他为软弱基床底层的取值。

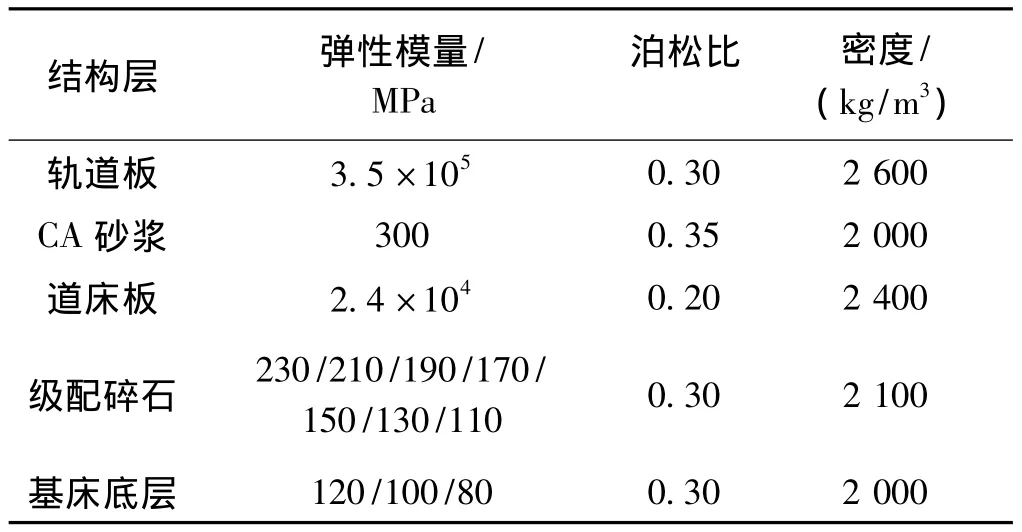
表1 模型材料计算参数

路基刚度不均匀按轨道板下路基端部不均匀和角部不均匀考虑，路基刚度不均匀分布形状及分析时选用的节点位置见图1。计算时不均匀部位从轨道板端部开始，长度从0逐渐增加到整个轨道板长度，共13种情况。对应于每一种长度，级配碎石层的弹性模量分别取 110，130，150，170，190，210 和 230 MPa 七种情况进行计算。

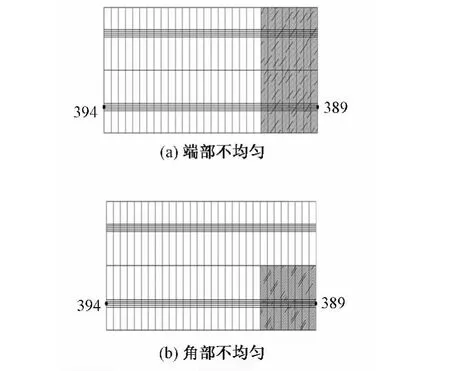
图1 路基刚度不均匀状况示意

3 模型动力响应分析

3.1 路基刚度不均匀部位对轨道动位移的影响

图2为轨道板下路基端部和角部不均匀部位刚度值为130 MPa时，轨道板两端节点最大动位移随不均匀部位长度的变化曲线。从图中可以看出，不论是不均匀端节点389，还是均匀端节点394，其动位移均随着不均匀部位长度的增大而增大，但端部不均匀情况的动位移更大，增加速率也更快。因此，在后面分析时路基刚度不均匀均按端部不均匀考虑。

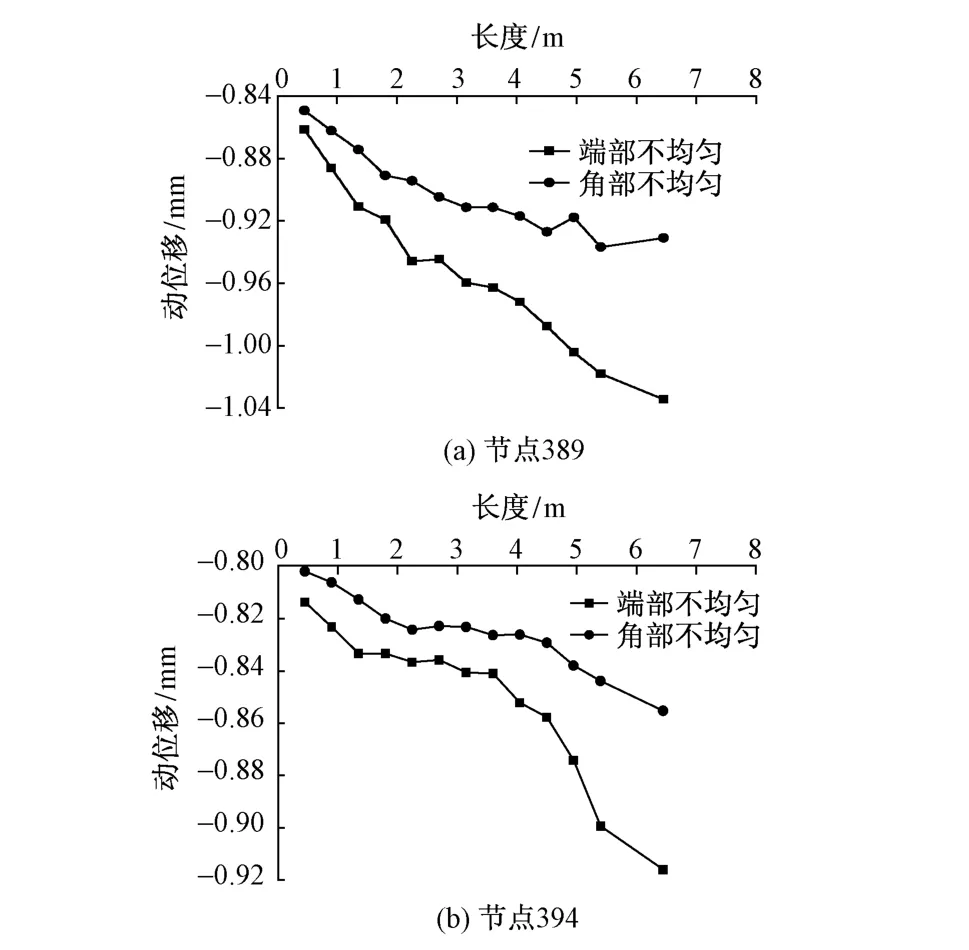
图2 路基刚度不均匀部位长度对轨道结构动位移的影响

3.2 路基刚度不均匀状态对轨道结构动位移的影响

图3为基床底层刚度为120 MPa时路基结构各种不均匀性状下轨道板端部节点最大动位移曲线。从图3(a)可以看出，节点389的动位移随刚度值的变化比较明显，并且随着不均匀区域面积的增加而增大。当级配碎石层不均匀区域刚度＜150 MPa后，轨道板节点动位移将超过1 mm，尤其是不均匀区域的刚度值为130 MPa和110 MPa时，变化更加明显。当不均匀区域刚度为130 MPa、面积达到5 m2，及不均匀区域刚度为110 MPa、面积达到3 m2时，轨道板节点动位移将超过1 mm。从图3(b)可以看出，只有当不均匀区域的面积达到10 m2后，节点394的动位移才有明显的变化，不均匀区域的刚度值为130 MPa和110 MPa时，变化更加明显。由此说明，路基刚度不均匀不仅影响本区域上部轨道结构的动位移，而且对其他满足要求的相邻区域上轨道板的动位移也会产生影响，且不均匀区域的刚度值越小，影响越明显。

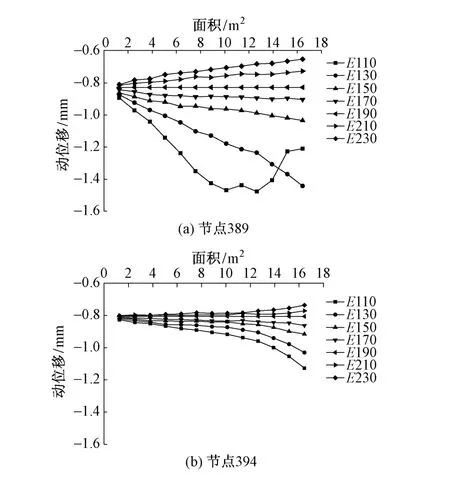
图3 基床底层刚度为120 MPa时轨道板端部节点动位移曲线

3.3 基床底层刚度对轨道结构动位移的影响

为了分析基床底层刚度对轨道结构受力及动位移的影响，本文还分析了当基床底层刚度为100 MPa，80 MPa时各种不均匀性状对轨道结构动力特性的影响。分析结果见图4和图5。

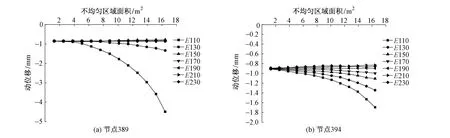
图4 基床底层刚度为100 MPa时轨道板端部动位移曲线

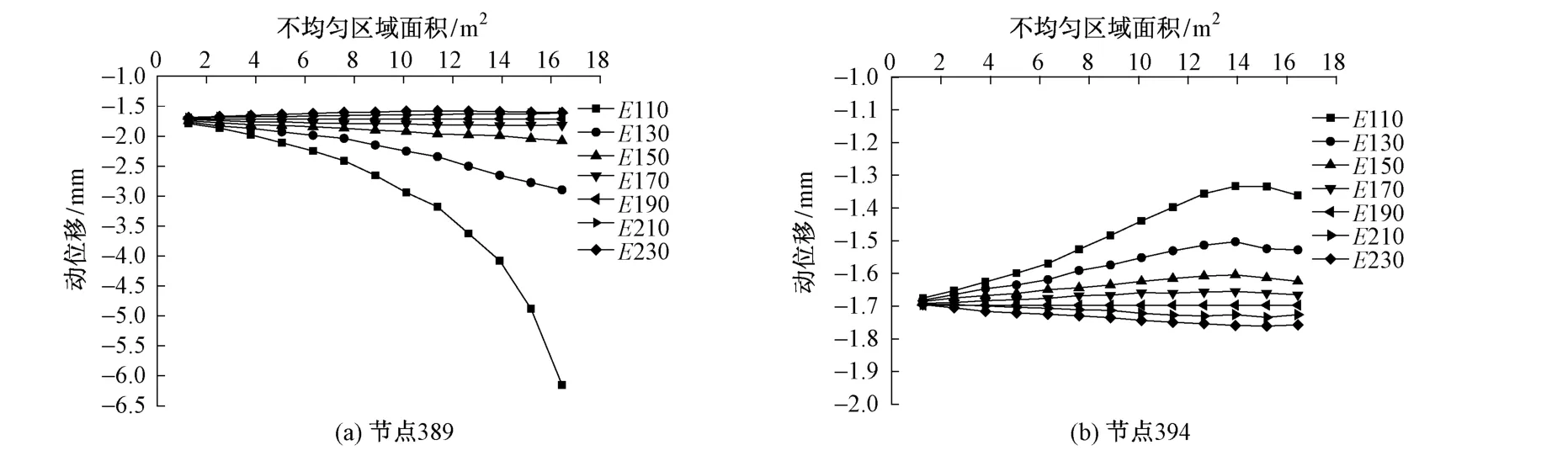
图5 基床底层刚度为80 MPa时轨道板端部动位移曲线

图4为基床底层刚度为100 MPa时路基不均匀状态下轨道板最大动位移曲线。从图4(a)可以看出，当级配碎石层刚度为150 MPa以上时，不管不均匀区域的面积多大，对节点389动位移的影响并不明显。但当级配碎石层刚度为130 MPa、不均匀区域的面积为10 m2，及级配碎石层刚度为110 MPa，不均匀区域的面积为5 m2后，轨道板动位移就明显增大，影响效果显著增加。从图4(b)可以看出，当基床底层刚度为100 MPa时，随着级配碎石层不均匀区域面积的增大和不均匀程度的增加，节点394的动位移随着级配碎石层刚度值的减小而有增加的趋势。当不均匀区域的面积较小时，动位移增加不太明显，但当不均匀区域的面积扩大到一定范围后，动位移增加较快。如当级配碎石层刚度为130 MPa、不均匀部位面积为8 m2，以及级配碎石层刚度为110 MPa、不均匀部位面积只有5 m2时，轨道板动位移超过1 mm。

图5为基床底层的刚度为80 MPa时路基不均匀状态下轨道板最大动位移曲线。图5(a)为节点389的最大动位移曲线，从图中可以看出，不管级配碎石层的刚度多大，轨道板节点的动位移都＞1.5 mm。图5(b)为节点394的最大动位移曲线，从图中可以看出，不管不均匀区域的面积有多大，轨道板动位移均不能满足要求，并且轨道结构动位移反而会随级配碎石层刚度值的增加而增大。由此可见，当基床底层刚度不满足要求时，仅仅依靠增加级配碎石层刚度值来达到合格的路基刚度值是不可能的。

3.4 路基刚度不均匀范围大小对轨道结构动应力的影响

图6为轨道板在不同基床底层刚度时各种路基不均匀情况下所承受的最大动应力。从图6(a)和图6(b)可以看出，轨道板所受的动应力均随着路基级配碎石层刚度的减小而增大，且变化趋势一致。但图6(c)的变化趋势一致性方面不如图6(a)和图6(b)明显，刚度超过正常值与小于正常值的变化规律也不一致，且动应力均比图6(a)和图6(b)中的动应力小。基床底层刚度小，对轨道结构的动应力有一定的缓冲作用，但动位移不能满足要求。

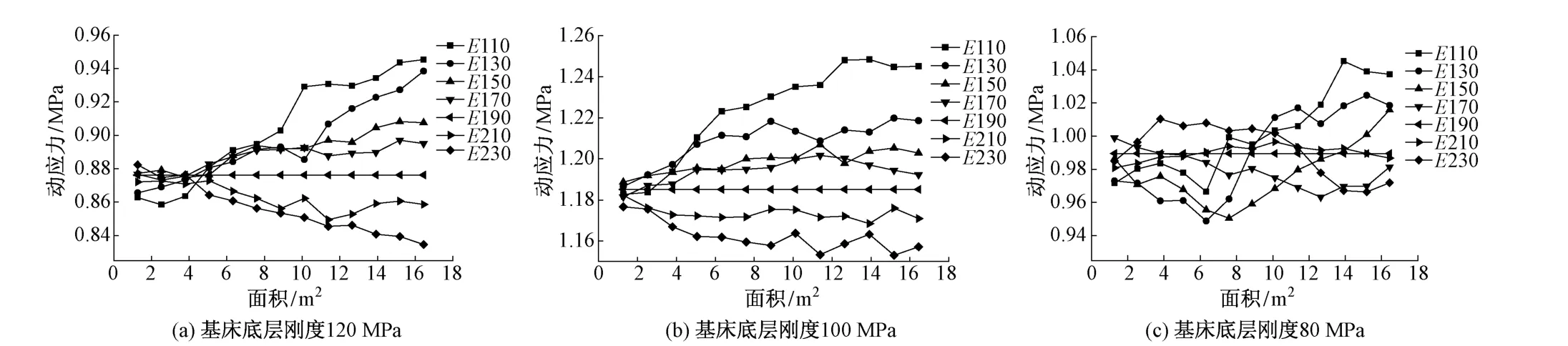
图6 轨道板在各种路基状态下的最大动应力

4 结论

通过建立无砟轨道—路基多层体系模型，分析了路基各种不均匀性状对轨道结构动位移和动应力的影响，得到如下结论:

1)轨道板端部下路基不均匀引起轨道板承轨槽位置处的动位移比角部不均匀情况稍大。

2)路基不均匀不仅影响其上部结构的动位移，并且对其相邻区域上部结构的动位移也有影响。

3)路基不均匀区域的面积较小时，对轨道板动位移影响不大，但当级配碎石层不均匀区域刚度为130 MPa、面积达到 5 m2，及不均匀区域刚度为110 MPa、面积达到3 m2时，轨道板两端节点动位移将超过允许值。

4)基床底层刚度对轨道结构动力特性影响较大。当基床底层刚度不满足要求时，仅仅依靠增加级配碎石层刚度值来满足要求是不可能的。

［1］韩义涛，姚力.基础沉降对土路基上板式轨道动力性能影响分析［J］.铁道工程学报，2007(10):28-31.

［2］蔡成标，徐鹏.高速铁路无砟轨道关键设计参数动力学研究［J］.西南交通大学学报，2010(4):493-497.

［3］刘茹冰，张士杰.路基沉降不均对板式轨道受力的影响分析［J］.路基工程，2009(1):142-143.

［4］陈鹏.高速铁路无砟轨道结构力学特性的研究［D］.北京:北京交通大学，2008.

［5］周萌，宫全美.路基不均匀沉降值对板式轨道动力响应的影响［J］.铁道标准设计，2010(10):1-4.

［6］马军旺.路基不均匀沉降对岔区无砟轨道结构力学特性的影响研究［D］.北京:北京交通大学，2011.

［7］徐庆元，李斌，周智辉.CRTS-Ⅰ型板式无砟轨道线路路基不均匀沉降限值研究［J］.中国铁道科学，2012，33(2):3-5.

［8］姜辉.路基不均匀沉降对无砟轨道结构受力影响分析［J］.中国科技财富，2009(6):47.