并置梁横向加固运营后剩余有效预应力研究

代金鹏，王起才，张戎令，葛 勇，赵礼刚

(兰州交通大学土木工程学院，甘肃兰州 730070)

我国在20世纪60～70年代末修建的钢筋混凝土简支T形梁桥，主梁截面尺寸偏小，设计荷载较低，一般都没有设置横向连接构造或是设置的横向连接比较薄弱，并置的梁体在列车荷载作用下，由于结构截面不对称，造成梁内外侧变形不一致，梁体产生斜弯曲变形，桥梁横向振动加剧，横向振幅严重超限［1］。

为保证列车的安全运营，对既有并置梁进行了横向体外预应力加固，加固后桥梁的横向振动明显减小，稳定性有了很大程度的提高。并置梁在加固后运营若干年，由于结构的横向变形及横向预应力筋松弛导致了桥梁再次出现横向振幅加大的现象。横向预应力的损失量、残余量及为保证结构安全应该补张拉预应力的量亟待研究。

目前常用的索力测定方法有压力表测试法、传感器测试法及振动法［2］。当需对施工完毕的拉索进行索力测试时，振动法几乎是目前唯一的选择［3］。振动法所用测试设备携带方便，容易安拆，可以重复使用，且在理论上有较为成熟的公式。但并置梁横向体外预应力加固钢绞线长度一般较短，多为2～5 m，复杂的边界条件及抗弯刚度对索力测试结果影响较大，能否用振动法来精确测试钢绞线的剩余有效预应力，是一个值得探讨的问题，本文将对此进行讨论和分析。

1 常用的振动法索力计算模型

振动法测定索力的理论基础是弦振动理论。假定索体为等截面且质量分布均匀，索在静力平衡位置做微幅平面弯曲振动，索振动模型如图1所示。

图1 索振动示意

应用动力学原理可以建立索在无阻尼时的自由振动方程。

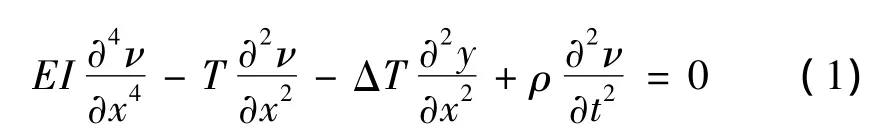
式中，EI为索的弯曲刚度，T为拉索拉力，ΔT为振动引起的索力变化，ρ为索单位质量。

1.1 索的张紧弦模型

该模型利用两端固定的张紧弦来模拟拉索，计算模型中不考虑索的抗弯刚度和垂度。由式(1)得索力

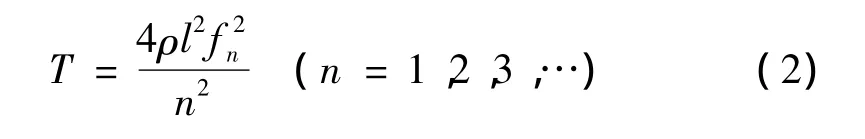
式中:l为索计算长度;fn为索振动第n阶固有频率;n为索振动频率阶次。张紧弦的频率之间成倍数关系，即各阶频率之比为1∶2∶3∶4…，则相邻频率的差值就等于基频，只要确定出频差或者判断出频率的阶次，就可以利用式(2)计算出索力。

1.2 索两端铰接

当索两端的边界条件可以简化为两端铰接时，ΔT的影响可以忽略［4］，解微分方程(1)得频率ωn为

此时索力的表达式为

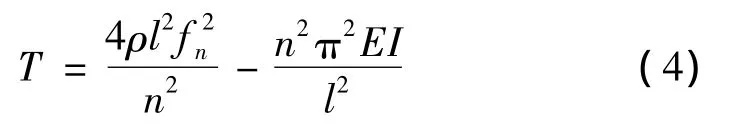
1.3 索两端固结

当索两端的边界条件可以简化为两端固结时，解微分方程(1)得频率方程为

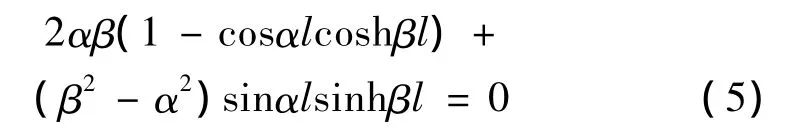
式中:

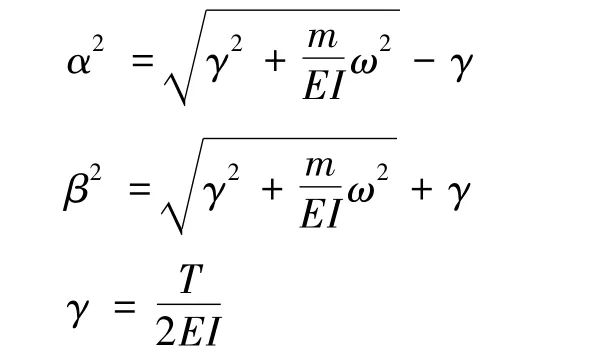
这是一个超越方程，需要通过数值方法求解。该方程形式较为复杂，不适于在现场检测索力时应用。

1.4 固支欧拉梁的振型函数

文献［5］以固支欧拉梁的振型函数作为两端固结拉索的振型函数，运用能量原理，给出了两端固结拉索索力计算的近似公式

对于简支边界条件取αn=βn=n;对于固支边界条件取 αn=n+0.1，βn=n+1。

从形式上看，在简支边界条件下，式(6)可以转化为式(4)。

2 索力计算模型的试验验证

2.1 索力试验

为验证上述理论的正确性、可靠性和适用性，设计了室内钢绞线拉索试验，自平衡试验架如图2所示。该试验模型有如下特点:试验用钢绞线长度可以调节;拉索更换方便快捷;穿心式压力传感器安放对索体振动影响较小;利用精密压力传感器配套静态应变测试仪来精确控制张拉应力。试验中采用附着在索体上的高精度加速度传感器来捕捉拉索的振动信号，通过滤波、放大和频谱分析，由频谱图来确定拉索自振频率。

图2 自平衡试验架

针对本文所研究的问题，测试l=2.1，3.3，4.5 m 3种不同长度钢绞线在不同张拉力下的自振频率。2.1 m钢绞线张拉力取31.060，39.984，72.471 kN;3.3 m钢绞线张拉力取49.509，59.837，71.167 kN;4.5 m钢绞线张拉力取9.703～215.853 kN。

2.2 试验结果分析

试验获取的钢绞线前3阶自振频率如表1所示。

表1 钢绞线自振频率 Hz

从表1中可以看出，钢绞线各阶自振频率近似成倍数关系，即从1阶到3阶频率之比近似为1∶2∶3。

索力计算结果如表2所示，索力计算值比较分析如图3所示。其中T0为穿心式压力传感器测试索力，T1为式(2)计算索力，T2为式(4)计算索力，T3为式(6)计算索力。

由表2及图5中索力计算值与实测索力值对比可知:式(2)索力计算值与实测值相差较大;式(4)考虑了钢绞线抗弯刚度的影响，索力计算模型对抗弯刚度的影响进行了修正，较式(2)索力测试精度有所提高，但总体来说索力计算值与实测值偏差较大，索力识别精度较低;式(6)计算索长＞3.3 m的钢绞线索力时，计算索力值与实测值偏差较小，最大不超过7.56%，计算索长＜3.3 m的钢绞线索力，偏差较大。当钢绞线长度＞3.3 m时，利用1阶频率计算索力，索力计算值小于实测值，最大偏差不超过－6.23%，利用2阶频率计算索力，索力计算的精度最高;当索长＜3.3 m时，利用公式(6)计算钢绞线索力，对计算索力进行0.75～0.85倍的折减，索力更加接近真实值。本文的研究结果可以作为一种测试经验，为相关的桥梁索力检测和健康评价提供参考。

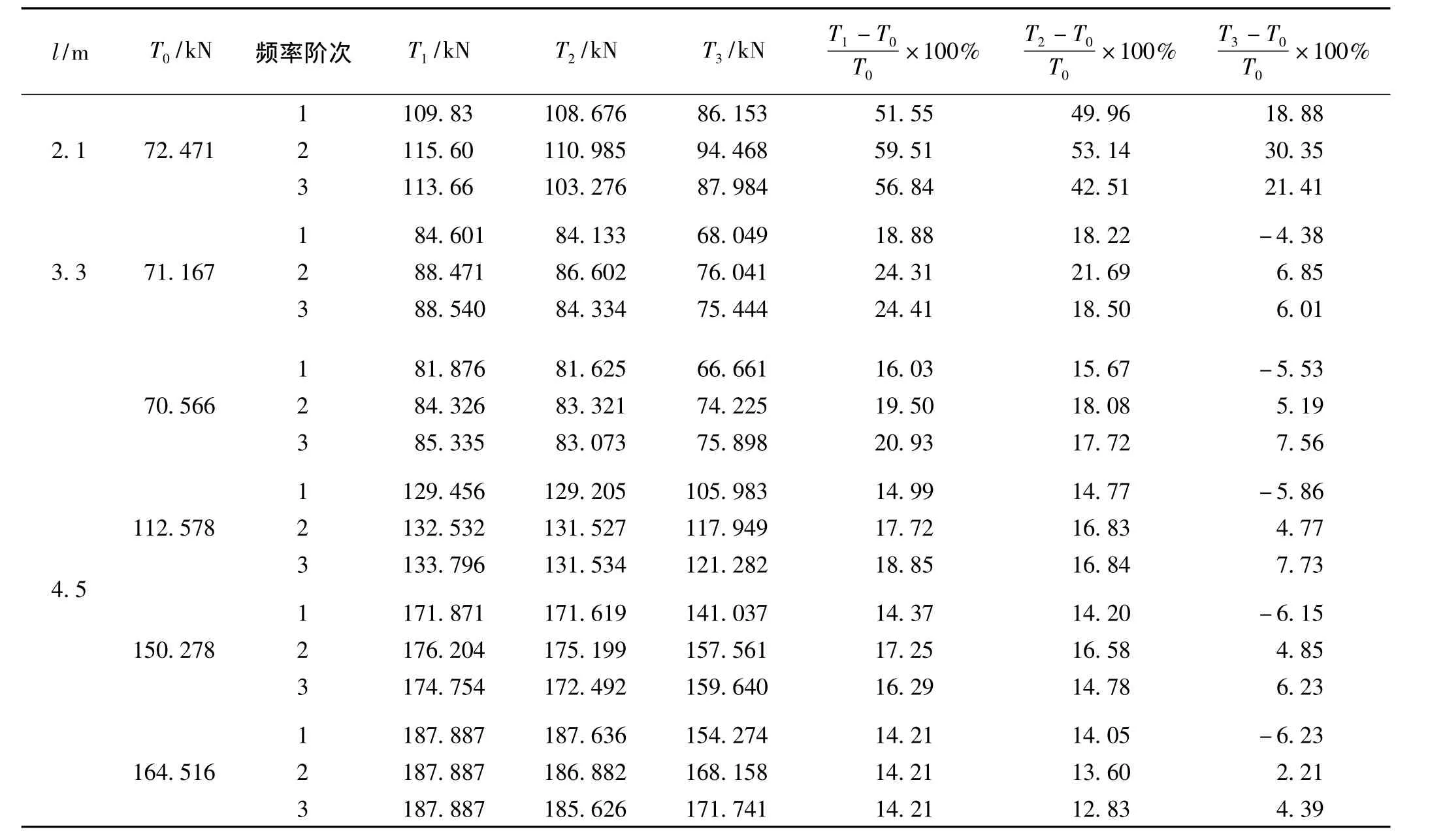
表2 计算索力与实测索力偏差比较

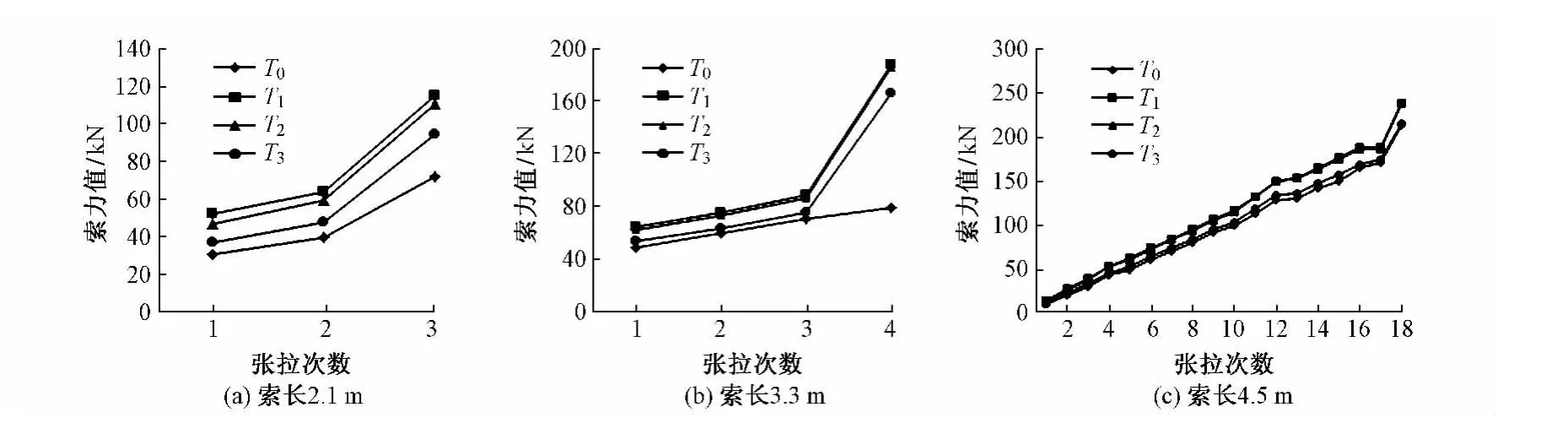
图3 不同索长2阶频率索力计算值

3 结论

1)预应力钢绞线各阶自振频率成倍数关系。索的张紧弦模型、两端铰接模型在较短钢绞线的索力测试中使用很难保证其测试精度。

2)文献［5］提出的钢绞线索力计算公式在索长＞3.3 m时索力识别精度较高，当索长＜3.3 m时要进行折减才能达到较高识别精度。

［1］付克民.中小跨铁路桥梁并置梁加固［J］.工程技术，2011(3):163-164.

［2］魏建东.索力测定常用公式精度分析［J］.公路交通技术，2004，2(21):53-56.

［3］林元培.斜拉桥［M］.北京:人民交通出版社，1994.

［4］吴晓亮.频率法在钢管混凝土吊杆拱桥索力测试中的研究与应用［D］.合肥:合肥工业大学，2010.

［5］甘泉，王荣辉，饶瑞.基于振动理论的索力求解的一个实用计算公式［J］.力学学报，2010，42(5):983-987.