反馈线性化移动电站非线性鲁棒励磁控制

刘 璞，邵天章，谷志锋

（军械工程学院车辆与电气工程系电力工程教研室，河北 石家庄 050003）

0 引 言

各种用电装备都要求在额定电压下运行才能发挥最大效能，因此保持供电电压稳定，是保证供电质量的主要手段之一。但是输出电压是经常变动的，尤其移动电站这种小型有限电网络比大电网电压波动更加严重[1]，电站运行工况的变化、外界环境的影响和负载的频繁切换都会对移动电站的运行状态产生较大影响。有效控制电站的励磁系统，保证输出电压对外界的干扰具有较强的抑制能力是当前迫切需要解决的问题。

文献[2-3]提出了基于船舶同步发电机励磁系统的智能控制，该控制与PID控制相结合可以在大负载变化时更好地稳定发电机端的电压，但是该控制主要依赖于发电机的线性化数学模型，而实际中模型包括干扰和参数的不确定性，具有很强的非线性。文献[4-5]将近代微分几何控制理论与电力系统的动态结构结合起来，利用零动态方法解决非线性控制问题，然而该方法不能有效解决存在干扰时的鲁棒性问题。

本文首先建立励磁系统的不确定性模型（如外部干扰），然后采用状态反馈精确线性化的方法将原非线性方程转化为线性方程，利用LMI工具箱求解线性方程，代入非线性方程求解原系统的鲁棒控制律，该控制器考虑了励磁系统的非线性和参数不确定性，对于提高励磁系统控制特性具有很好的促进作用，参考军用移动电站参数，最后通过Matlab/Simulink仿真分析，验证该控制器对干扰的抑制能力。

1 同步发电机模型的建立

本文中采用的同步电机模型为常用的三阶励磁模型，该模型忽略暂态凸极效应，忽略饱和[6]：

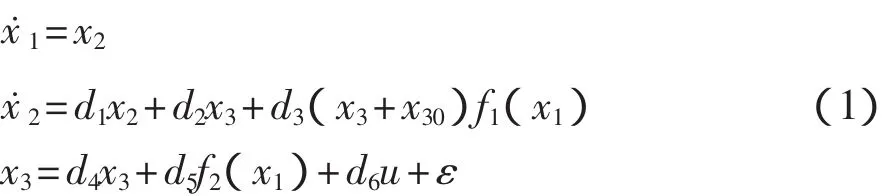
式（1）中：

式中：δ——发电机功角；

ω——发电机角速度；

xd——直轴电抗；

xT——变压器电抗；

xL——传输线电抗；

H——机组的转动惯量；

u=Vf-Vf0，Vf——励磁控制量；

Vf0——对应于[δ0ω0]T的初始励磁控制量；

ε——励磁绕组的电磁干扰。

该模型保留了电机模型中的非线性部分和不确定部分，能够较为完整地反应电机在实际运行过程中的状态。

2 非线性鲁棒控制的实现

式（1）中的电机数学模型可以用下述非线性方程表示[7-9]：

其中：

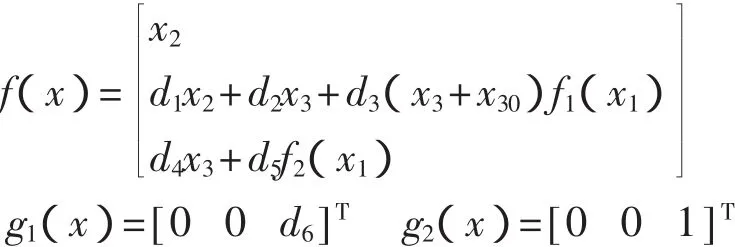
1）将非线性系统化为线性系统，选取输出为y=h（x）=x1，根据状态反馈精确线性化的条件判断是否能进行线性化，首先观察输出对非线性方程的关系度r：

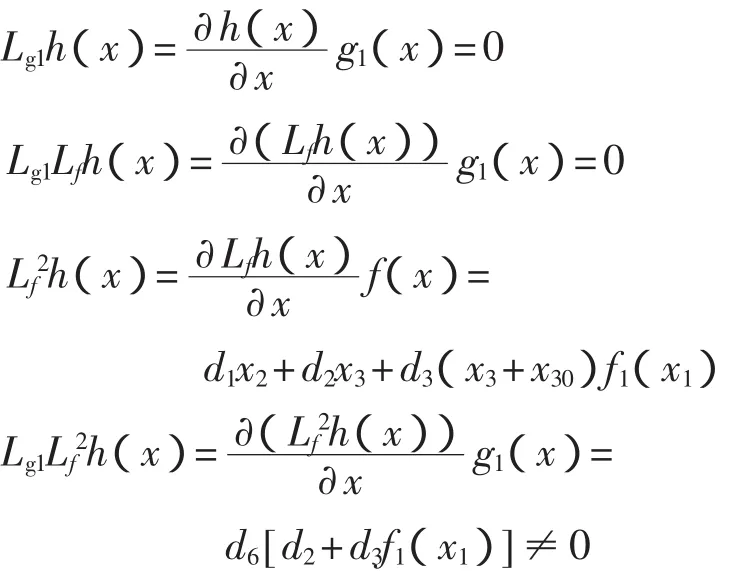
设d2+d3f1（x1）≠0所以r=n=3，满足精确线性化条件，选择如下坐标变换ψ：

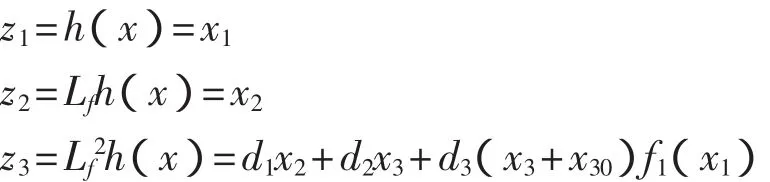
其Jacobian矩阵Je为

该Jacobian矩阵在d2+d3f1（x1）≠0时非奇异，说明新的坐标（z1，z2，z3）能够作为一组基坐标，因此在坐标（z1，z2，z3）下可以进行线性化变换，即：

2）在坐标变换ψ作用下，原系统可以表示为

则式（2）可写为

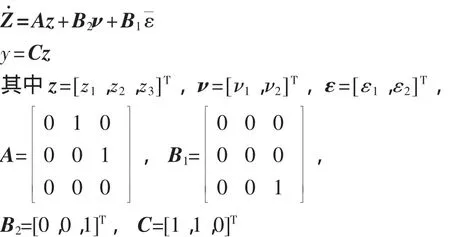
3）求解线性鲁棒控制律，原非线性方程就变换为上述线性方程，对于上述方程，可以根据H∞控制理论求解其鲁棒控制规律。该线性方程的鲁棒控制问题有解的条件是当且仅当Riccati不等式

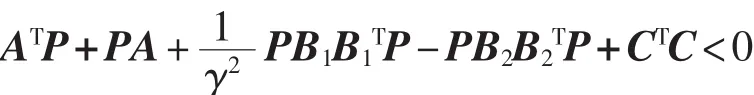
有一个非负解P*，利用Matlab中LMI工具箱中的feasp求解，求得一个非负解

4）求解原非线性系统的鲁棒控制律u*，由于

在原坐标下的控制律

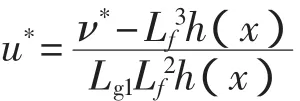
所以原系统的非线性鲁棒控制律即为

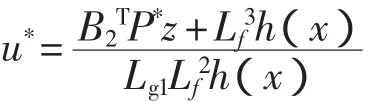
励磁电压

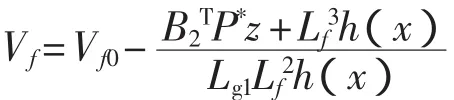
3 仿真分析

为验证上述控制规律，进行了仿真测验。励磁系统的仿真参数[10]：xd=0.8258，=0.1045，H=2.05s，=1.05 s，xT=0.029 2，xL=0.026 6，D=0.15，干扰抑制常数γ=3。

仿真1：分析该控制器对由负载变化引起的干扰的抑制能力。电站初始带负载10 kW，在0 s时突加5kW的负载，其励磁电压、转速、功角的变化曲线与PID控制器对比如图1所示。

由图1中不难看出，鲁棒控制器的励磁电压调节时间只需2 s，而PID控制时间增加到了4 s，鲁棒控制器的转速超调量只有0.005，而PID控制的超调量达到了0.035，功角的变化曲线也说明了鲁棒控制器的控制效果比PID控制效果要好。在负载发生变化时，鲁棒控制器能迅速调节恢复到稳定状态，该控制器对由于负载变化引起的干扰有较强的抑制能力，具有很好的鲁棒性能。

仿真2：γ参数的变化对控制器的影响。根据控制器的设计原理，γ值越小，对干扰的抑制能力越强，图2代表了不同γ取值的励磁电压的变化。

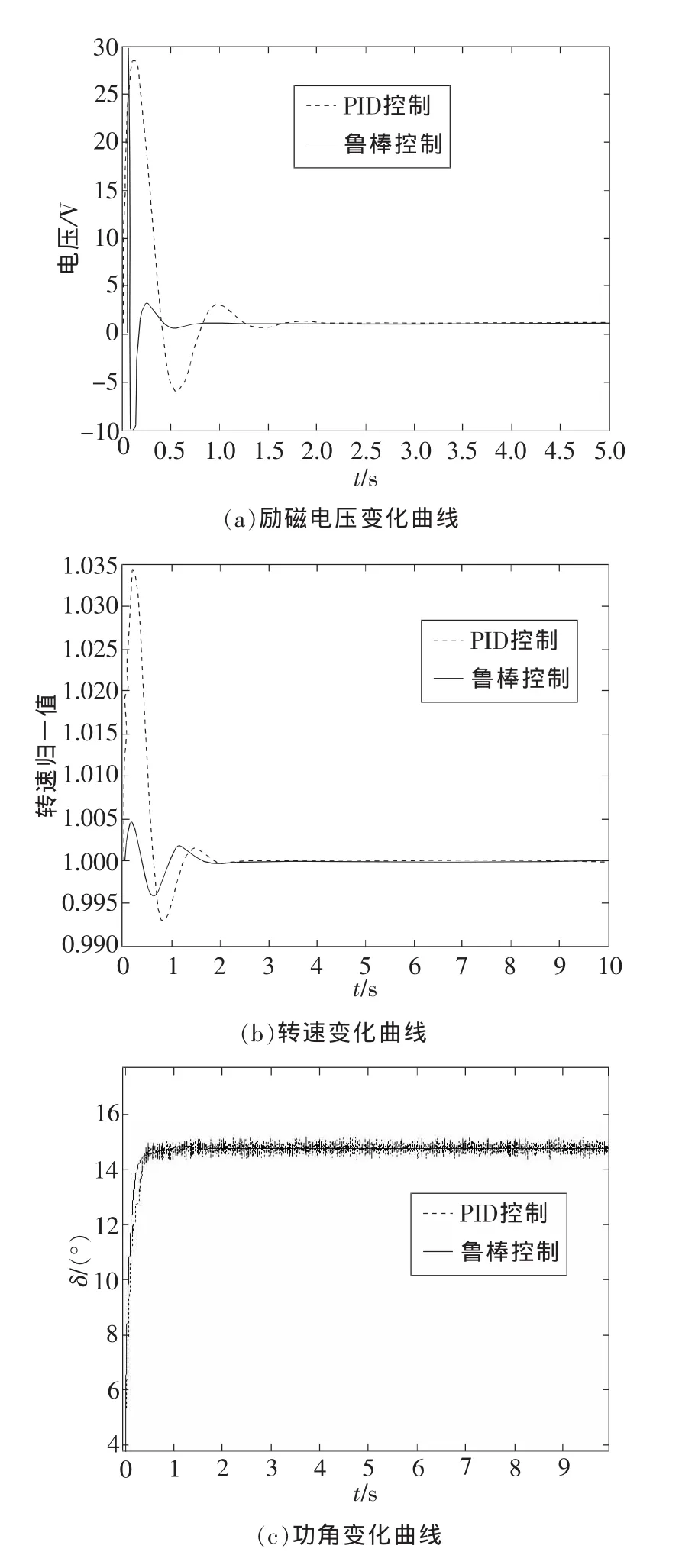
图1 突加负载时励磁电压、转速、功角变化曲线

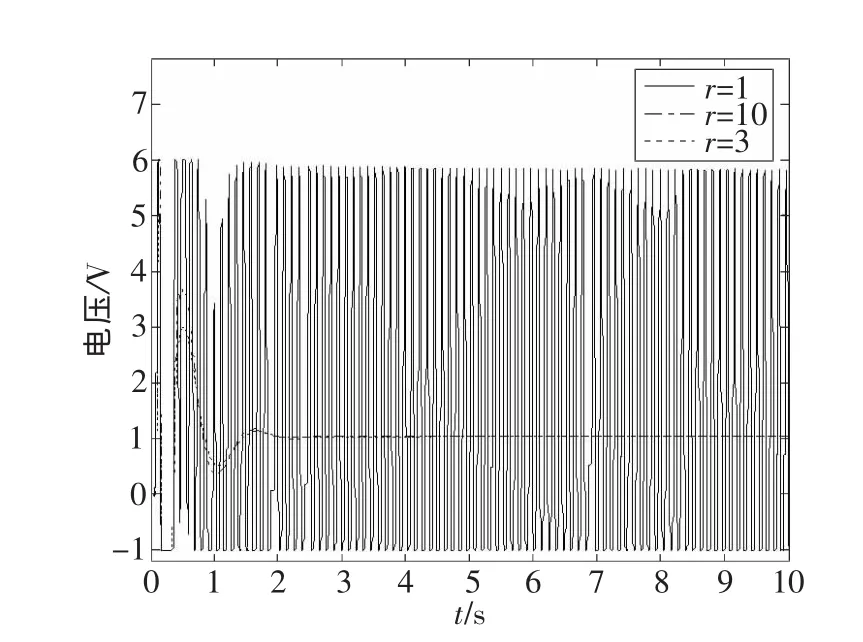
图2 γ值不同时励磁电压变化曲线

从图2中可以看到，γ取值并不是越小越好，γ取值较小时，励磁电压就会发生振荡，影响实验效果，γ取值过大，对干扰的抑制能力就会较弱，因此在仿真1中选取γ=3。

4 结束语

对于电站来说，稳定问题即动态安全问题是极其重要的问题。本文通过对含有干扰和不确定参数的同步电机数学模型进行状态反馈精确线性化，得到其鲁棒控制规律，结合实际电站参数，利用Matlab/Simulink进行仿真分析，通过与传统PID控制器的对比，该控制规律能够有效地抑制振荡，提高系统的动态稳定性，显示出了较好的鲁棒性能，而后还对γ的选取对系统的影响进行了仿真，说明合理选择γ对系统动态性能具有较大的作用。

[1]籍凤荣，胡玉贵.内燃机电站励磁系统分析[M].北京：解放军出版社，1994：9-14.

[2]孙才勤，郭晨.大型轮机模拟器中船舶电力系统的建模和仿真[J].系统仿真学报，2009（11）：3251-3254.

[3]程木军，孙才勤.智能PID控制器在船舶发电机控制中的应用[J].大连海事大学学报，2006（2）：5-8.

[4]栗春，姜齐荣.静止无功补偿器的非线性控制器的设计[J].电网技术，1998，22（6）：34-38.

[5]马幼捷，周雪松.静止无功补偿器非线性控制对系统功角的影响 [J].中国电机工程学报，2003，23（12）：84-88.

[6]梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用[M].北京：清华大学出版社，2008：296-301.

[7]卢强，梅生伟，孙元章.电力系统非线性控制[M].北京：清华大学出版社，2008：148-164.

[8]周双喜，汪姓盛.基于直接反馈线形化的非线性励磁控制器[J].中国电机工程学报，1995，15（4）：281-288.

[9]王锡淮，郑天府，肖健梅.带电压调节的非线性鲁棒励磁控制策略研究[J].电力自动化设备，2007，27（8）：38-41.

[10]刘金森，朱灵子.发电机励磁系统建模与仿真[J].贵州电力技术，2011，14（2）：1-3.