水轮发电机不平衡磁拉力计算

李建伟，庞立军，贾 伟，田 超

(哈尔滨大电机研究所，黑龙江 哈尔滨 150040)

0 引言

发电机正常运行时，转子在均匀磁场中运行，定子和转子之间的气隙均匀。此时定转子径向各点所受的磁拉力是均匀的，其在径向上所受合力为零。这种均匀的磁拉力对定转子的刚度有加强作用。实际上，由于制造质量或安装不当，就会引起定转子之间气隙的不均匀。此时，定转子就会受到沿径向激发的电磁力。由于这种电磁力是气隙不均衡引起的，故称之为不平衡磁拉力。不平衡磁拉力引起的故障对电机的运行产生较大的影响，将会导致系统产生振动和噪声，加快电机主轴的磨损，缩短电机寿命，对于柔性转子，可能造成定转子的接触。因此，研究不平衡磁拉力对定转子的影响，直接关系着电机动力学和系统稳定性的研究[1－2]。

不平衡磁拉力产生的原因可归结为以下几类:1)由于定转子不同心、定子内腔或转子外圆有缺陷、转子质量偏心、大轴不直以及转子匝间短路等等;2)由于定子分数槽次谐波磁动势、定子并联支路内环流产生磁势、分块定子合缝不好、定子绕组固定不够等原因引起定子以极频或整倍数频振动。虽然产生不平衡磁拉力的原因较多，但主要可归结为电机中磁路和电路的不对称所致[3]。

国外对不平衡磁拉力的研究工作开展较早。1900年，Behrend[4]提出假设，气隙中的磁密与气隙长度成反比，对不平衡磁拉力进行了讨论，得出磁拉力的线性表达式。接下来的一段时间内，众多学者从不同角度获得了与Behrend关系相近的一些结果，无一例外的都是线性关系。直至上世纪90年代开始，更多的学者从不同的理论和实验研究结果出发，发现不平衡磁拉力和偏心之间存在复杂的非线性关系。1996年，曲凤波、孙玉田[5]通过电磁场有限元计算发现偏心与不平衡磁拉力之间存在着3次函数的非线性关系。姜培林[6]通过保角变换简化边界条件，使用气隙磁导来计算气隙磁密，推导出不平衡磁拉力的非线性表达式。2003年，郭丹[7]把气隙磁导展开为级数的形式，通过转子或定子表面的Maxwell应力积分计算得到不平衡磁拉力的非线性解析表达式。

不平衡磁拉力对定转子系统振动特性的的研究非常关键，因此有必要对各不平衡磁拉力的计算进行分析和对比。本文研究了不平衡磁拉力几种表达式，为进一步深入研究定转子系统不平衡磁拉力下的低频振动及其动力学特性提供研究基础。

1 不平衡磁拉力的计算方法

1.1 线性解析表达式

计算气隙不均匀产生的电磁拉力的传统方法是利用经验公式，根据结构形式的不同而得出。多年来，不均匀磁拉力简化成与偏心率成正比的线性关系[1]可以表达为如下形式:

其中L和D为转子长度和直径，m;B为磁密度，T;β为系数，它与发电机的类型、磁场分布、槽、阻尼和绕组结构等有关。一般为0.2至0.5，e为偏心距，δ为正常间隙，m。

另外的一个不平衡磁拉力的线性表达式是王跃方[8]从系统的磁场储能出发得到的:

令 Km= βDB2π/2μ0δ，其力学意义是单位长度的转子发生单位偏心时所受的磁拉力，磁拉力与转子直径D、气隙磁密的平方B2和偏心e成正比，而与气隙的大小δ成反比，并且磁路饱和程度越高(即β值越小)，磁拉力数值就越小。

1.2 非线性解析表达式

由于线性模型误差较大，采用数值方法计算结果准确但过于繁琐，人们一直希望建立电磁拉力的非线性近似公式。曲凤波[5]等在数值分析的基础上建立的近似计算公式为:

Kδ卡式系数，K1，K3待定系数。K1=0.8 ～1，K3=0.9 ～1.5。

姜培林[6]通过保角变换将电磁场的边界条件简化，得到磁势的解析表达式，磁通和磁势梯度的函数，而磁拉力从表面积分可以得到。考虑空载场，假设定子转子铁心的磁导系数为无穷大，气隙中转子的磁位为0，磁势降为定值F0，气隙中磁力线垂直于转子表面，不平衡磁拉力及其刚度可表示成:

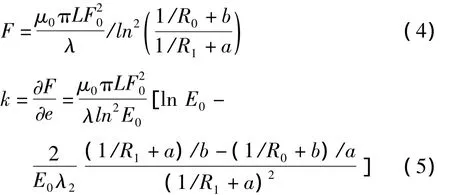
计算不平衡磁拉力的完全表达式常常通过一常数加上余弦函数形式模拟气隙变化，然后转换为Fourier级数的形式。气隙基波磁动势的表达式为一已知幅值的正弦或余弦函数，不平衡磁拉力的计算可以采用以下方法[2]。

电机偏心转子气隙示意图见图1。设转子中心距定子中心的距离为r，方向角为γ，转子与定子间气隙的位置角为α，则偏心转子与定子间的气隙近似为如下表达式:

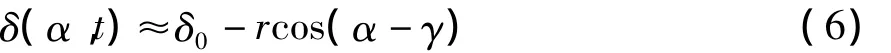
其中δ0为转子不偏心时的平均气隙长度。气隙磁导为:

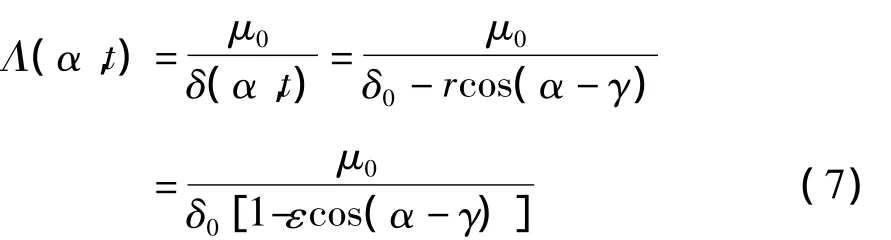
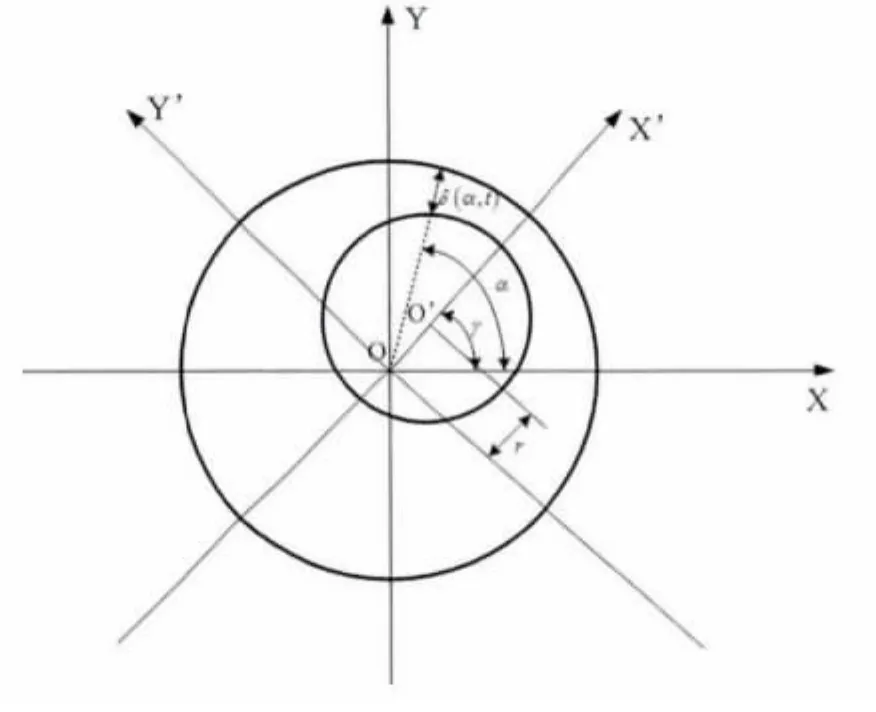
图1 电机偏心转子气隙示意图

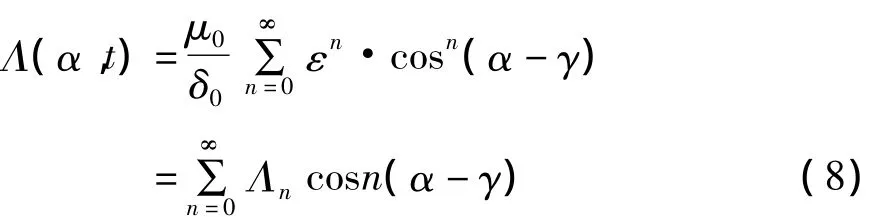
式中展开系数为:

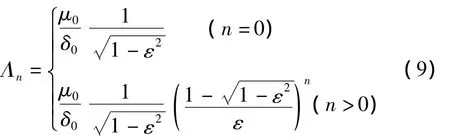
在水轮发电机中，气隙基波磁场对于电磁振动影响较大，谐波磁场尤其是高次谐波磁场对于电磁振动影响较小。因此，我们仅考虑气隙基波磁势的影响。根据电机原理，空载时三相同步电机的气隙基波磁动势可表达为:

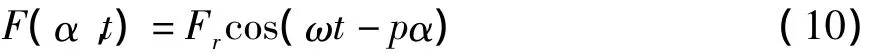
式中，Fr为转子激磁电流的基波磁动势，p为电机的磁极对数，ω为电频率。对于水轮发电机，电频率ω与转子转动角速度Ω和电机对数p满足Ω=ω/p。由电磁场理论可知，气隙磁密B有如下表达式:

垂直气隙与转子(空气与铁心)边界的Maxwell应力为:

其中，μ0为空气中的导磁系数。由于水轮发电机组磁极对数往往较多，一般远大于3，所以气隙磁导级数展开到3级就足够了。可由Maxwell应力在转子表面积分求的不平衡磁拉力和为:

转子长度和直径分别为L及R。

2 不平衡磁拉力及其刚度计算方法的比较

从以上对不平衡磁拉力的表达式推导来看，

1)两个线性的不平衡磁拉力的表达式，都与转子直径D、气隙磁密的平方B2和偏心e成正比，而与气隙的大小δ成反比，非常相似。不平衡磁拉力下的系统刚度是对偏心的导数。显然，二者在其他参数一定的情况下，不平衡磁拉力下的刚度为一常数;

2)上述3种不平衡磁拉力的非线性解析表达式，采用的假设和简化方法各不相同:

曲凤波的3次函数表达式，基本假设是:1)由于水轮机发电极数很多，定子铁心内径较大，而定转子相对偏心量与定子铁心内径相比小得多，而在一个极域内由偏心引起的气隙变化很小;2)由于求解区域为一个极，每极下定子槽数简化为整数。

姜培林对数表达式的假设为:假设定子转子铁心的磁导系数为无穷大，气隙中转子的磁位为0，磁势降为定值F0，气隙中磁力线垂直于转子表面。

级数展开的非线性表达式的前提假设是:转子偏心距沿转轴长度不变。

3)在偏心很小的情况下，线性和非线性不平衡磁拉力的计算结果非常接近，而对于较大偏心的情形，线性表达式的计算结果的误差很大。根据姜培林模型的计算结果来看，较大的偏心被定义成了4 mm。

3 算例

计算选取典型的SF320－48－12800－G型电机，其基本参数如表1所示。

表1 电机的基本参数

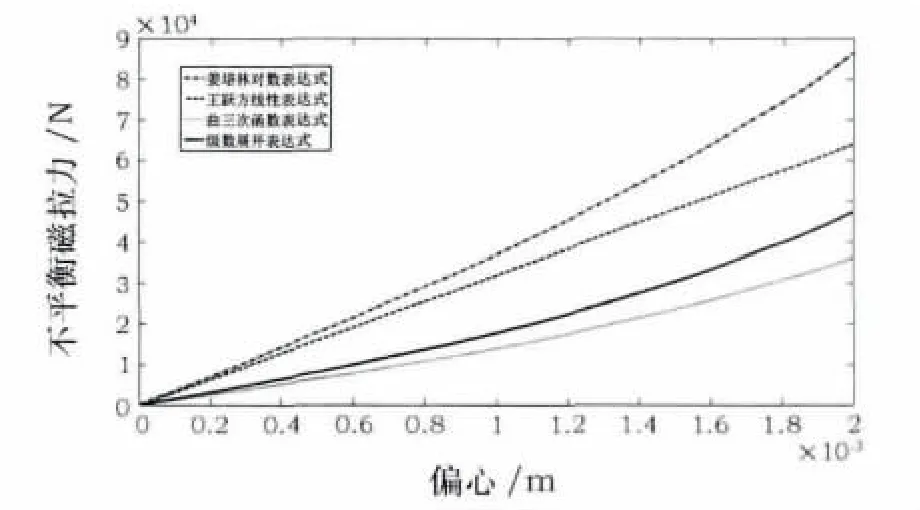
图2 不平衡磁拉力随转子偏心的变化

转子相对于定子的偏心在0～2 mm变化时，4种关系(两种线性关系只选取了一种)就该电机中的不平衡磁拉力随偏心的变化曲线对比如图2所示。可以看出，4种关系下的不平衡磁拉力出现偏差发生的位置远小于4 mm。而到了偏心2 mm，4种关系下的不平衡磁拉力范围则3.6～8.64 T，偏差很大。

不平衡磁拉力随气隙的变化如图3所示。在偏心一定的情况下，不平衡磁拉力与平均气隙之间存在着反比关系(除姜培林的对数函数表示的不平衡磁拉力外)。

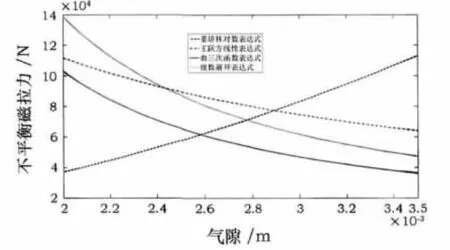
图3 不平衡磁拉力随气隙的变化

4 防止不平衡磁拉力的措施

由于制造和装备技术的限制，不平衡磁拉力不可能完全消除。由不平衡磁拉力的计算结果来看，可从以下两个方面削弱不平衡磁拉力:

1)降低转子和定子之间的相对偏心。提高定子、转子、轴承的加工正确性和配合。对于已经出现的转子不圆，可调整磁极的胶木垫，对松动的线圈则需要加绝缘垫片紧固。

2)适当的增加平均气隙。从上节的分析来看，适当地增大气隙，可有效地降低不平衡磁拉力。

5 结语

定子和转子之间气隙的不均产生了不平衡磁拉力。实际的制造和装配过程中，不可避免地会产生不平衡磁拉力。分析和对比了几种线性和非线性不平衡磁拉力的计算模型。线性和非线性不平衡磁拉力的在很小的偏心下就会产生明显的差别，非线性不平衡磁拉力之间也存在着差别，包括建立模型的假设和计算的结果上。降低定子和转子之间的相对偏心和适当增加平均气隙能够有效的降低不平衡磁拉力。

[1]郭丹，冯辅周，诸福磊，何永勇.水轮发电机组电磁振动研究综述[C].第十届全国设备监测与诊断技术学术会议，2000，5:399－403.

[2]金鑫.基于ANSYS的水轮发电机机电耦合弯曲振动响应仿真[D].长春:吉林大学，2011.

[3]白晖宇，荆建平，孟光.电机不平衡磁拉力研究现状与展望[J].噪声与振动控制，2009，12(6):5 －7.

[4]B A Behrend.On the mechanical force in dynamics caused by magnetic attraction trans[J].AIEE，1900，Vol.17:617 － 620.

[5]曲凤波，孙玉田，曲大庄.水轮发电机的不平衡磁拉力[J].大电机技术，1997，4:1 －3.

[6]姜培林，虞烈.电机不平衡磁拉力及其刚度的计算[J].大电机技术，1998，4:32 －34.

[7]郭丹，何永勇，诸福磊.不平衡磁拉力及对偏心转子系统振动的影响[J].工程力学，2003，20(2):116－121.

[8]王跃方，黄丽华，胡家炘.磁拉力对电机转子动力学特性的影响[J].力学与实践，1996，18(4):32－34.