永磁同步电机幂次变速趋近律积分滑模控制

茅靖峰，吴爱华，吴国庆，张旭东

（南通大学电气工程学院，江苏南通 226019）

永磁同步电机幂次变速趋近律积分滑模控制

茅靖峰，吴爱华，吴国庆，张旭东

（南通大学电气工程学院，江苏南通 226019）

为了提高永磁同步电机转速伺服控制性能，针对伺服系统模型参数不确定和外部扰动强的特点，利用基于趋近律设计方法的滑模控制理论，设计了一种永磁同步电机转速伺服积分滑模控制器。滑模面函数中的状态偏差积分项，确保了转速跟踪稳态无静差；通过引入非线性幂次组合函数构造的基于跟踪偏差的变速趋近律，使得切换增益具有随系统偏差自适应调整的特性，并可有效抑制滑模控制输出的抖振。经与转速伺服PI控制器对比实验表明，变速趋近律积分滑模控制器具有更好的动、静态特性和鲁棒性。

永磁同步电机；伺服控制；积分滑模；变速趋近律；幂次组合函数

1 引言

永磁同步电机（PMSM）结构简单、功率密度大、效率高、转矩惯量比大，目前在中小功率的交流伺服系统中获得了广泛应用。然而，PMSM伺服系统是一个多变量、强耦合的非线性系统，对于一些高性能伺服控制的应用场合，采用针对局部线性化模型和基于固定参数优化匹配的传统PI控制策略，在PMSM系统参数变化以及快速大负载扰动的影响下，不易取得理想的伺服控制效果。为此，多种非线性控制方法，如变参数PI控制［1］、自适应控制［2］、学习控制［3］、内模控制［4］、鲁棒控制［5］、自抗扰控制［6］、预测控制［7］、滑模控制［8-10］等被用来提高PMSM转速伺服控制性能。

滑模控制（SMC）无需精确的对象模型，可根据系统当前的状态，以跃变的控制方式迫使系统沿设定的“滑动模态”运动。具有响应速度快、对参数及外加干扰不灵敏、控制器易于工程实现等优点，适合PMSM伺服控制需求［8-11］。但在SMC控制的实际系统应用中，提高稳态跟踪的控制精度、抑制滑模控制律符号函数引起的抖振，以及合理选取切换函数的增益是常需要关注的问题。

本文根据基于趋近律方法的滑模控制器设计理论，采用积分型滑模面结构和幂次组合函数趋近律方法设计了一种永磁同步电机（PMSM）滑模转速伺服控制器。该方法具有切换增益随系统偏差自适应调整的特性，并在保证伺服跟踪控制精度的基础上，切换控制输出无抖振。通过仿真与实验结果验证，设计的滑模控制器在PMSM系统较广的运行空间内均能有效提高系统的动静态品质，性能优于常规固定参数PI控制器。

2 PMSM伺服系统模型

假设气隙磁场正弦分布、磁路不饱和，忽略铁芯涡流和磁滞损耗，永磁同步电机在d-q旋转坐标系下的数学模型可表示为

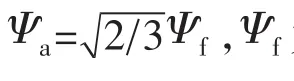
电磁转矩方程

机械运动方程

式中：J为转动惯量；Bm为摩擦系数；TL为负载转矩。

对于表贴式PMSM有Ld=Lq=L，且在id=0的磁场定向控制条件下，机械运动方程可重写为

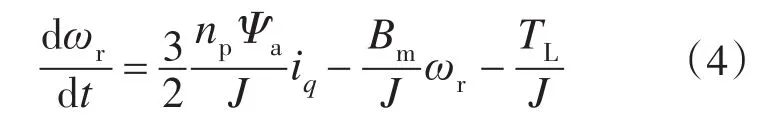
针对PMSM转速伺服控制系统，其控制器设计的目的为选择合适的控制律，使得电机在任何负载转矩工况下，实际转速ωr快速准确地跟随给定转速。为此，定义转速误差

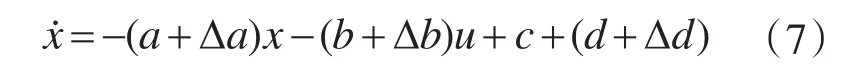
式中：Δa，Δb，Δd分别为电机参数摄动量。

现令广义扰动项η=-Δax-Δbu+Δd，并假设满足|η|≤H，H为正实数。式（7）可简化为

3 积分滑模控制器设计

3.1 传统滑模控制

滑模控制器设计包括两个相对独立的步骤：设计滑模面函数s(x)，使它所确定的滑动模态渐进稳定且具有良好的动态品质；设计滑模控制律u±(x)，使到达条件得到满足，从而在滑模面s(x)=0上形成滑动模态。

对于PMSM转速伺服系统式（8），选取积分滑模面函数

式中：kp，ki＞0为滑模面系数，决定最终滑模状态的品质。

当系统状态处于滑模面上时，s(t)=s˙(t)=0，即

求解式（10），可得

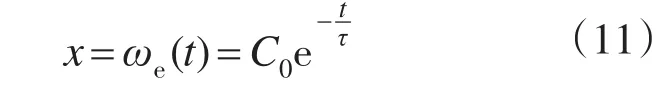
式中：C0为任意常数；τ为收敛时间常数，τ＝kp/ki。

由式（11）可知，积分滑模面函数式（9），可以使系统偏差按照指数曲线形式衰减至零，从而实现无超调的转速跟踪控制。因此，可以通过被控PMSM电机的固有电磁响应时间来合理选取偏差的收敛时间常数τ，进而计算得到积分滑模面的系数取值，即可达到理想的转速无静差跟踪控制效果。

选取等速趋近律

其中，ε，k＞0，k的作用是改善系统的动态品质，适当调节该参数能够改变系统向滑模面的趋近速度；符号函数的增益参数ε是系统克服摄动及外干扰的主要参数。

由式（8）和式（9）可解出标称系统的滑模控制律

根据Lyapunov稳定性条件，当条件ss˙＜0满足时，系统在整个状态空间都趋向于滑模面，并在进入滑动模态后以选定的趋近规律渐近到达稳态。该条件即是求取控制律u±(x)的依据。

为此，对式（14）求导，并由式（8）和式（13）可得：

因此，选取ε＞kpH，则恒有ss˙＜0。即控制律式（13）满足滑动模态的到达条件，能够驱使系统沿着滑模线s趋近于平衡原点。

进一步分析式（13）可知，正是符号函数sgn（s）这一部分切换控制律，因其理论上的理想瞬时继电特性，保证了系统对不确定性和外加干扰η的鲁棒控制，且ε越大，系统克服摄动和外干扰的能力就越强。但显然，在滑模面s（x）=0附近，对于实际系统，因符号函数sgn（s）在物理实现上的动作滞后延时，造成了控制律u的大幅切换，导致了实际系统的抖振现象，如图1所示。

为了抑制控制器输出大幅切换引起的系统抖振，造成控制性能下降和执行器损坏，常采用连续化方法，将控制律中的符号函数sgn（s）由饱和函数sat（s）代替。

3.2 幂次组合函数趋近律方法

文献［12］提出非线性幂次组合函数fal（s，α，δ），并成功地将传统加权和型PID控制，改造成非线性组合型PID控制。fal（s，α，δ）函数表达式为

式中：0＜α＜1；δ＞0。

图2所示为幂次组合函数fal（s，α，δ）、饱和函数sat（s）和符号函数sgn（s）的特性比较曲线。

显然，由特性比较曲线图2可见，当0＜α＜1时，fal（s，α，δ）函数的输出光滑连续，在较小的s取值区间（|s|＜δ），具有较大的增益，随着s取值的增大（|s|≥δ），其增益逐渐减小。即所谓的“小误差，大增益；大误差，小增益”的良好非线性工程特性。因此，fal（s，α，δ）函数的输出特性非常适用于滑模控制“大范围逼近，柔和趋近”的控制要求。

图1 实际系统的抖振示意图Fig.1 Chattering phenomenon in practical systems

图2 3种函数的输出特性Fig.2 Output characteristics of three kinds of functions

综上分析，在PMSM转速伺服滑模控制器中，考虑幂次组合变速趋近律

选取Lyapunov函数式（14），当|s|＞δ时，

显然，式（18）和式（19）均满足Lyapunov稳定性条件，ss˙＜0。因此，幂次组合变速趋近律式（17）能够将系统引导到滑动模态上，并在系统状态轨迹向滑模面趋近过程中，fal（s，α，δ）的幅值逐渐衰减，呈现出随系统偏差大小而自适应调整切换增益的特性，并很快趋向于零，最终使系统稳定于平衡原点上。

为此，根据式（17），并结合式（8）和式（9）解出的基于幂次组合变速趋近律的滑模控制律为

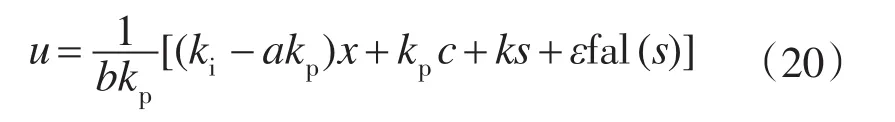
4 仿真与实验

4.1 仿真分析

依据前文分析，应用Matlab/Simulink建立PMSM基于id=0的磁场定向解耦策略的速度伺服控制系统。PMSM的参数为：定子电阻Rs=2.4 Ω，定子电感Ld=Lq=6.35 mH，转动惯量J=1.33 kg·m2，粘滞摩擦系数B=0.000 1，永磁体磁链Ψf=0.35 Wb，极对数np=4，额定转速nN=2 500 r/min，额定转矩TN=5 N·m。

针对PMSM的毫秒级的电磁响应时间，依据式（11）的特性分析，可选取转速偏差的收敛时间常数τ=0.1 ms，则积分滑模面参数可通过优选设计为kp=1，ki=10 000。

选取幂次组合变速趋近律参数α=0.5，δ=0.1，k=400，ε=820。

图3为PI和SMC控制下系统转速阶跃跟踪响应波形，给定转速=120 rad/s。

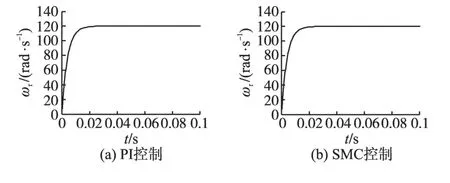
图3 转速阶跃响应曲线Fig.3 Speed step response curves

由图3可以看出，在系统无干扰和参数摄动条件下，通过细致调节PI参数，PI控制和SMC控制均可使得电机有良好的转速跟踪特性。

图4为PI和SMC控制下，电机在120 rad/s恒定转速工况时，0.4 s时刻突加额定负载转矩的转速偏差和控制器输出响应曲线。

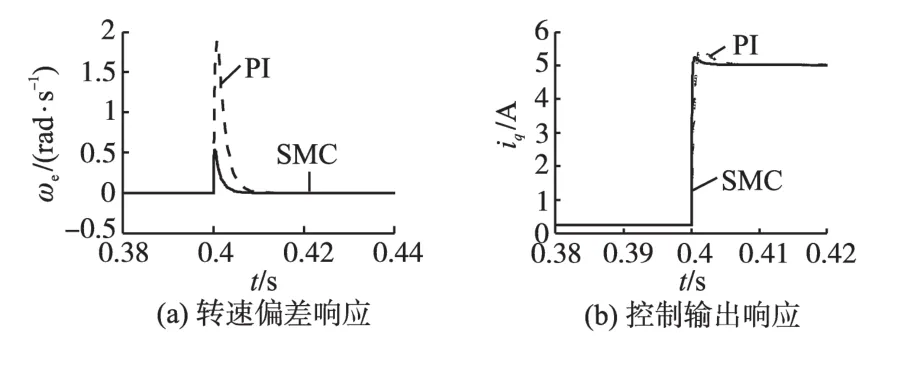
图4 负载转矩突变响应曲线Fig.4 States response curves caused by load torque change

由图4可以看出，在PI控制下，系统的转速偏差最大值和调节时间均约为SMC控制的4倍，且SMC控制量输出超调小、响应迅速、平滑无抖振。可以表明，SMC控制较PI控制在负载扰动的转速波动幅值和平抑速度上，具有更好的抑制能力。

图5为PI和SMC控制下，电机在120 rad/s恒定转速、带额定负载工况时，0.5 s时刻电机参数摄动量Δa，Δb和Δd同时发生20%增幅情况下的系统转速波动的动态过程，以及滑模面的迁变过程。

由图5可以看出，在系统参数摄动后，积分型SMC可以快速地调节滑模面的状态，并较PI控制，在偏差波动的幅值和偏差消除的时间上具有更好的表现。可以表明，SMC控制可以比PI控制更有效地抑制系统参数变化，且其输出稳态无静差。

图5 系统状态参数突变响应曲线Fig.5 States response curves caused by parameters change

另外，对比分析图3以及图4a和图5a发现，针对标称系统而优选的PI控制参数，虽然可使得PI控制和SMC控制在系统标称情况下达到近似相同的良好控制效果，但对于系统受干扰和参数摄动条件的控制效果，SMC控制强于PI控制。说明SMC控制的大范围适应性和鲁棒性强于PI控制。

仿真结果表明：1）由于滑模面函数的积分项作用，使得系统在负载大扰动和参数摄动后，电机转速跟踪控制输出稳态无静差；2）由于采用了幂次组合变速趋近律方法，使得SMC输出平滑无抖振，控制效果优于PI控制；3）通过滑模面函数及其参数的优化配置，系统的控制效果在电机标称态和非标称态之间具有良好的协调能力，大范围适应性和鲁棒性良好。

4.2 实验结果

利用基于DSP的PMSM伺服控制系统实验平台进行算法验证，其控制系统结构如图6所示。

图6 控制系统结构原理图Fig.6 Control system structure schematic diagram

实验中，电机的负载转矩加载利用磁滞测功机来实现，通过HX-901型转矩转速器和TR-2B型测量仪和读取转速和转矩数据。

图7a为PMSM在0.25 N·m恒定负载下，转速跟踪120 rad/s的启动阶跃响应曲线。图7b为PMSM在60 rad/s恒转速条件下，加载2 N·m负载转矩时的转速转矩响应曲线。

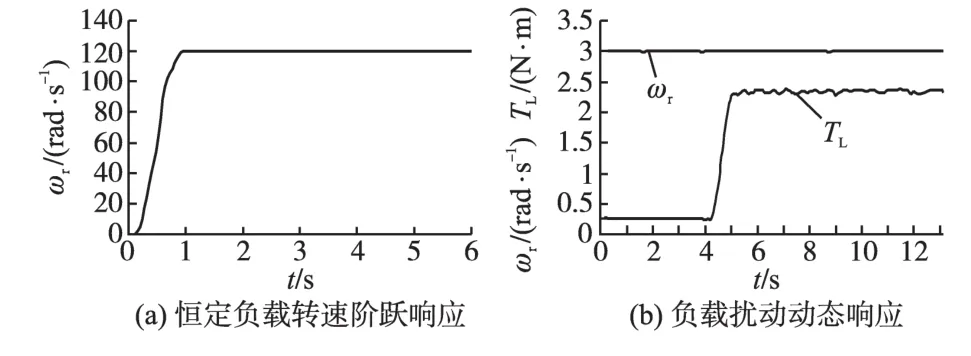
图7 转速伺服控制实验波形Fig.7 Speed servo control experiment waveforms

由图7可以看出，在SMC控制下，PMSM转速跟踪响应快速、无超调，稳态精度较高，抑制负载扰动的鲁棒性较强。

5 结论

仿真和实验结果表明，基于幂次组合变速趋近律积分滑模控制器，能够有效地抑制传统滑模控制律符号函数引起的抖振现象，并使得切换函数的增益具有随系统偏差大小而自适应调整的特性。在永磁同步电机转速伺服控制应用中，较传统PI控制器在跟踪速度、稳态精度、抑制参数摄动和大范围负载扰动影响的适应性和鲁棒性方面具有更好的动静态性能表现。

［1］ 孙强，程明，周鹗，等.新型双凸极永磁同步电机调速系统的

变参数 PI控制［J］.中国电机工程学报，2003，23（6）：117-123.

［2］ Han Ho Choi，Nga Thi-Thuy Vu，Jung Jin-Woo.Digital Im-plementation of an Adaptive Speed Regulator for a PMSM［J］.IEEE Transactions Power Electronics，2011，26（1）：3-8.

［3］ 李兵强，吴春，林辉.基于参考输入学习的永磁同步电机高精度位置伺服系统［J］.中国电机工程学报，2012，32（3）：96-102.

［4］ Li Shihua，Gu Hao.Fuzzy Adaptive Internal Model Control Schemes for PMSM Speed-regulation System［J］.IEEE Trans-actions on Industrial Informatics，2012，8（4）：767-779.

［5］ 杨书生，钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计［J］.中国电机工程学报，2009，29（3）：84-90.

［6］ 鲁文其，胡育文，梁骄雁，等.永磁同步电机伺服系统抗扰动自适应控制［J］.中国电机工程学报，2011，31（3）：75-81.

［7］ 王伟华，肖曦，丁有爽.永磁同步电机改进电流预测控制［J］.电工技术学报，2013，28（3）：50-55.

［8］ 张碧陶，皮佑国.基于分数阶滑模控制技术的永磁同步电机控制［J］.控制理论与应用，2012，29（9）：1193-1197.

［9］ 张晓光，赵克，孙力，等.永磁同步电动机滑模变结构调速系统新型趋近率控制［J］.中国电机工程学报，2011，31（24）：77-82.

［10］ 汪海波，周波，方斯琛.永磁同步电机调速系统的滑模控制［J］.电工技术学报，2009，24（9）：71-76.

［11］ Mao Jing-feng，Wu Guo-qing，Wu Ai-hua，et al.Nonlinear Decoupling Sliding Mode Control of Permanent Magnet Lin-ear Synchronous Motor Based on a-th Order Inverse System Method［J］.Procedia Engineering，2011，15（1）：561-567.

［12］ 韩京清.自抗扰控制技术［J］.前沿科学，2007，1（1）：24-31.

修改稿日期：2013-12-17

Integral-type Sliding Mode Control for PMSM with Power Variable Rate Reaching Law Method

MAO Jing-feng，WU Ai-hua，WU Guo-qing，ZHANG Xu-dong
（School of Electrical Engineering，Nantong University，Nantong226019，Jiangsu，China）

An integral-type sliding mode speed control for permanent magnet synchronous motor（PMSM）servo system was proposed to improve speed servo dynamic quality.The speed controller was designed based on variable rate reaching law method，and some system uncertainties including in model parameters and external disturbances were also considered.The integral term in the sliding mode surface function can ensure the speed tracking control without steady error.Due to the new variable rate reaching law algorithm designed by power combination function，the gain of the switch function was granted the capability of automatic adjust with tracking error，and the chattering amplitude can be progressively damp.Simulation and experimental results show that the proposed speed controller has a better stability，transient and robustness compared with that of PI controller.

permanent magnet synchronous motor（PMSM）；servo control；integral-type sliding mode；variable rate reaching law；power combination function

TM351；TP273

A

国家自然科学基金（61004053，61273151）；江苏省高校优势学科建设工程资助；江苏省高校研究生科研创新计划项目（CXLX13_681）；南通市应用研究计划项目（BK2012009，BK2013062）

茅靖峰（1976-），男，博士，副教授，Email：mao.jf@163.com

2013-08-01