城镇污水处理厂清洁生产等级评价二元语义模型与方法

王丽玲,张树深,张 芸 (大连理工大学环境学院,工业生态与环境工程教育部重点实验室,辽宁 大连 116024)

城镇污水处理厂清洁生产等级评价二元语义模型与方法

王丽玲,张树深*,张 芸 (大连理工大学环境学院,工业生态与环境工程教育部重点实验室,辽宁 大连 116024)

为解决城镇污水处理厂清洁生产等级评价问题,采用定性分析与定量计算相结合的方法,着重构建了城镇污水处理厂清洁生产等级评价指标体系及其权重确定方法;利用线性加权综合评价方法、模糊数学和二元语义概念,建立了城镇污水处理厂清洁生产等级评价模糊综合模型,并据此提出级别特征值概念,进而建立城镇污水处理厂清洁生产等级评价的二元语义模型与方法.实例计算分析说明,文中建立的清洁生产等级评价二元语义模型与方法可操作性强,等级评定结果比采用隶属度最大原则更直观、更便于解释,具有很好的应用与推广价值.

污水处理；清洁生产；模糊综合模型；二元语义；等级评价

污水处理厂是现代化城镇必须配套建设的一项重要的基础设施,污水处理尤其是深度处理对于缓解水域污染、改善水环境至关重要[1-3].但是,污水处理厂不同的处理工艺和管理模式(管理水平)在投入与处理效果方面区别较大.此外,对环境产生的二次影响也有较大差异.因此,对污水处理厂提出一套包含处理工艺、环境管理、污染物产生与排放等的清洁生产等级评价指标体系,进而建立污水处理厂的清洁生产等级评价模型是很有必要的[4-6].

近年来,我国的清洁生产工作广泛开展,环境保护部等相关部委相继出台了50多个行业的《清洁生产指标体系》和《清洁生产标准》.但目前清洁生产工作的重点还是放在制定各类工业企业的清洁生产指标与标准上,而缺乏工业企业清洁生产等级评价模型与方法等方面的研究.如何合理构建工业企业的指标体系与等级评价模型是国内外一个亟待解决的重要理论和实际课题[7-10].为此,本文以污水处理厂清洁生产为研究背景,在合理构建城镇污水处理厂清洁生产等级评价指标体系的基础上,利用模糊多属性(或指标、因素)[11]综合评价模型与二元语义概念[12-13],建立污水处理厂清洁生产等级评价的综合模型及方法,旨在为我国新型城镇化进程中环保治理企业的清洁生产等提供一条新的发展途径.

1 污水处理厂清洁生产等级评价指标体系构建

本文根据污水处理的特点[14-15],构建了城镇污水处理厂清洁生产等级评价指标体系.具体地,本文构建的城镇污水处理厂清洁生产等级评价指标体系是一个包含三层次三等级的递阶结构,其中一级评价指标有6个,包括处理工艺与设备要求(O1)、资源与能源利用(O2)、出水控制(O3)、污染物产生控制(O4)、废物回收利用(O5)和环境管理要求(O6);二级评价指标包括污水处理工艺总体要求(O11)、消毒工艺(O12)等24个;三级评价指标包括BOD5(O311)、COD(O312)、COD去除率(O322)等13个;评价等级分为3个级别:Ⅰ级(e1),Ⅱ级(e2)和Ⅲ级(e3).

污水处理厂清洁生产各级评价指标基准值取值原则是根据当前国际及国内污水处理厂的实际运行和管理情况,合理确定Ⅰ级、Ⅱ级和Ⅲ级基准值.确定Ⅰ级基准值时,参考国际清洁生产指标领先水平,以当前国内5%的企业达到该基准值要求为取值原则.确定Ⅱ级基准值时,以当前国内20%的企业达到该基准值要求为取值原则.确定Ⅲ级基准值时,以当前国内50%的企业达到该基准值要求为取值原则.对于定性评价指标基准值无法划分级别时,统一给出一个基准值[16].通过查阅文献资料及调查国内外污水处理厂的实际运行数据及管理情况[17-18],确定各个清洁生产等级评价指标要求或标准值,见表1.

2 清洁生产等级划分标准与评价指标权重的确定

2.1 清洁生产评价等级与划分标准

用ek(k=1,2,…,h )表示清洁生产的第k个等级,且规定并符号上表示为:ek>ek+1,即清洁生产的第k个等级ek比第k+1个等级ek+1强(或好).

根据当前污水处理行业工艺技术、设备水平、管理水平、污水处理相关标准及清洁生产的要求,将评价等级分为3个级别即h=3,其中等级e1代表国际清洁生产先进水平、e2代表国内清洁生产先进水平、e3代表国内清洁生产一般水平.

2.2 清洁生产评价指标权重的确定

根据污水处理厂实际数据和清洁生产评价指标对污水处理行业清洁生产实际效益和水平的影响程度及实施的难易程度,并咨询行业领域专家的意见,确定污水处理厂清洁生产评价指标权重,见表1.

表1 城镇污水处理厂清洁生产指标及其要求Table 1 Cleaner production evaluation indexes and requirements of town sewage treatment plants

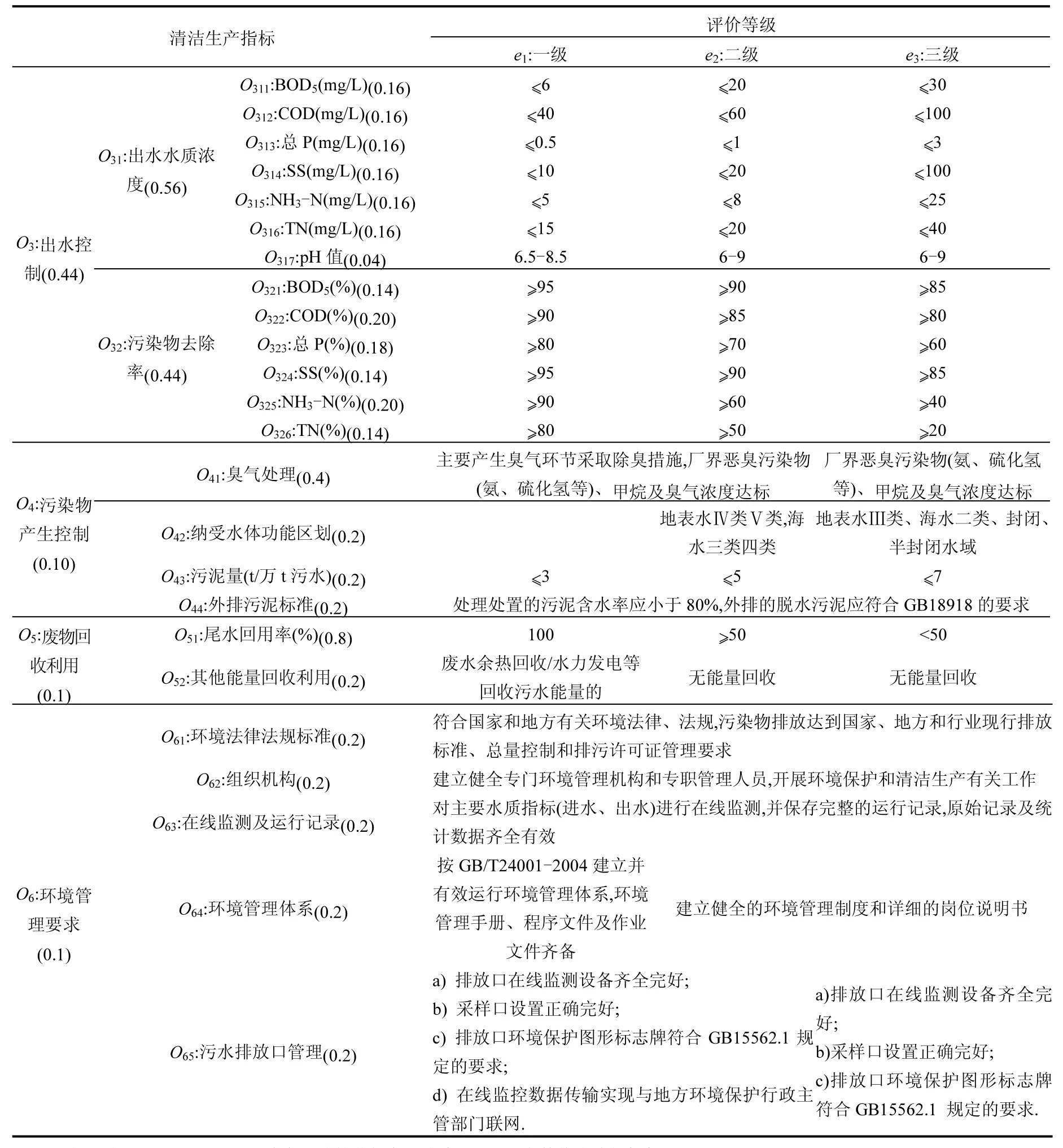
续表1

3 清洁生产评价指标等级隶属函数的确定

清洁生产评价指标通常可分为定量与定性评价指标两大类.

3.1 定性评价指标等级隶属函数的确定

对于定性评价指标,根据污水处理行业清洁生产的实际特点与要求,污水处理厂At(t= 1,2,…,N)关于定性评价指标Oijl(l=1,2…,Lij)的等级隶属函数可定义为:

式中:µtijlk表示污水处理厂tA关于第i个一级评价指标Oi(i=1,2,…,m)下第j个二级评价指标Oij(j=1,2,…,ni)的第l个三级评价指标(定性)Oijl隶属于第k个清洁生产等级ek的程度.在本文中,考虑3个污水处理厂即N=3,并分别记为A1、A2和A3,且由表1可知,m=6,n1=8,n2=3, n3=2,n4=4,n5=2,L31=7,L32=6,其他Lij=0.

式(1)是针对三级评价指标给出的等级隶属函数.但从表1可见,除评价指标O3(即出水控制)有三级评价指标以外,其他5个一级评价指标都只有二级评价指标.不难看出,式(1)同样适用于二级定性评价指标的等级隶属函数确定问题.

3.2 定量评价指标等级隶属函数的确定

对于效益型评价指标(即评价指标值越大,清洁生产等级越高),污水处理厂At关于定量评价指标Oijl的等级隶属函数可分别选取为:

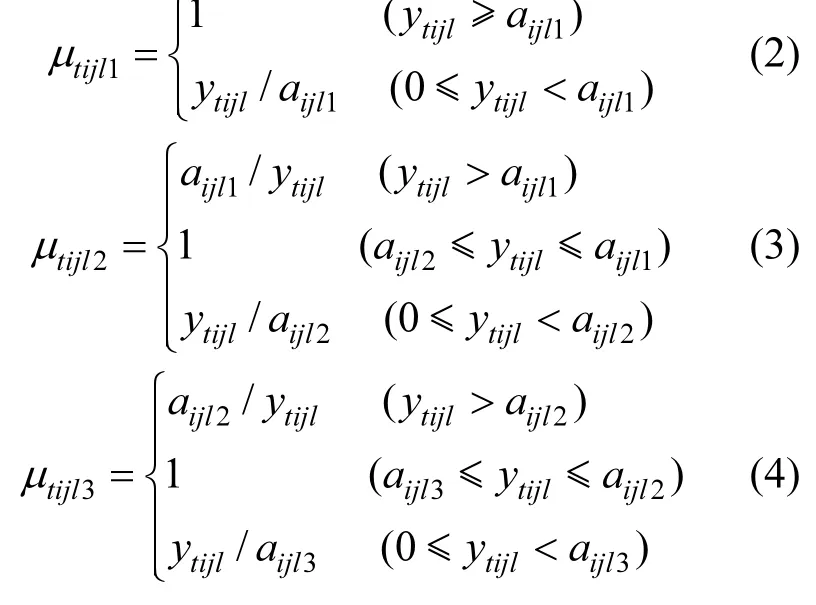
图1 效益型评价指标的等级隶属函数Fig.1 Grade membership function of profit evaluation index

式中:ytijl表示污水处理厂At关于第l个三级(定量)评价指标Oijl的值;aijlk表示Oijl属于等级ek(k=1,2,…,h )的基准值,在本文中h=3(否则可类似处理);µtijlk的含义与式(1)相同,见图1.

类似地,对于成本型评价指标(即评价指标值越小,清洁生产等级越高),污水处理厂At关于定量评价指标Oijl的等级隶属函数可分别选取为:

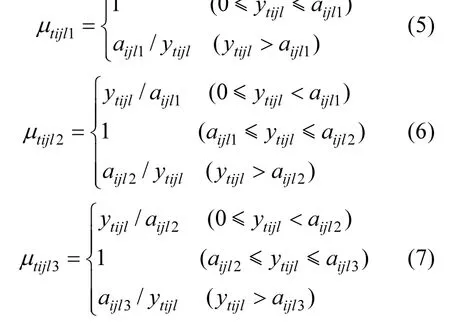
如图2所示.

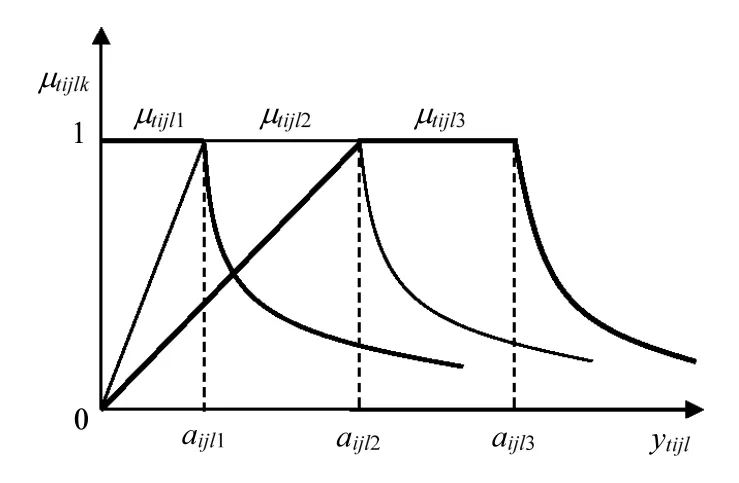
图2 成本型评价指标的等级隶属函数Fig.2 Grade membership function of cost evaluation index

当定量评价指标的等级基准(或划分)值为同一数值或同一区间值时,污水处理厂At关于定量评价指标Oijl的等级隶属函数可选取为:

4 清洁生产等级评价综合模型及其二元语义方法

根据清洁生产与城镇污水处理厂的实际情况及特点,针对定性与定量评价指标,分别利用式(1)～式(8),可计算得到污水处理厂At关于评价指标Oijl的等级隶属度µtijlk,通常用等级隶属度矩阵表示为µtij=(µtijlk)Lij×h.这是进行城镇污水处理厂清洁生产等级评价的基础数据.

类似地,表1可把一、二、三级评价指标的权重分别表示为下面的权重向量:

4.1 清洁生产等级评价模糊综合模型与方法

模糊线性加权综合评价方法是一种原理比较简单、便于计算的常用方法.本文针对清洁生产等级评价的内在要求及其具有的三层评价指标结构特征,借鉴模糊线性加权综合评价方法的思想,提出了城镇污水处理厂清洁生产等级评价模糊综合模型与方法.具体方法与步骤如下:

第一步:计算污水处理厂tA关于二级评价指标Oij对于等级ek的综合隶属度为:

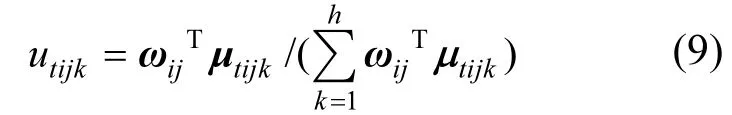
式中:µ=(µ,µ,…,µ)T为等级隶属度矩Lijk阵µtij的第k个列向量.于是,可得到At关于Oij对于所有等级ek的综合隶属度向量utij=(utijk)1×h.因此,可得At关于Oi下所有二级评价指标的等级隶属度矩阵µˆti=(utijk)ni×h.为叙述方便,仍把µˆti记为µti.

第二步:计算污水处理厂At关于一级评价指标Oi对于等级ek的综合隶属度为:

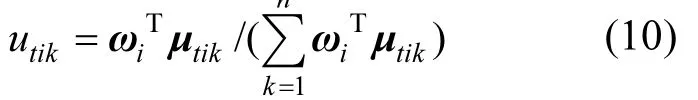
式中:µ=(µ,µ,…,µ)T为等级隶属度矩

ik阵µti的第k个列向量.于是,可得到At关于Oi对于所有等级ek的综合隶属度向量uti=(utik)1×h.因此,可得At对于所有m个一级评价指标的等级隶属度矩阵µt=(utik)m×h.为统一起见,把µt中的元素utik仍记为µtik.

第三步:计算污水处理厂At对于等级ek的综合隶属度为:

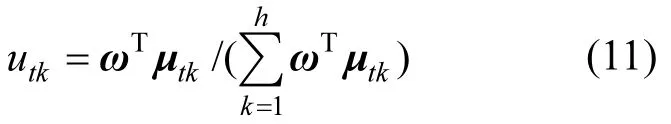
式中:µ=(µtkt1,µkt2,…,µktmk)T为等级隶属度矩阵µt的第k个列向量.于是,可得到At对于所有等级ek的综合隶属度向量ut=(utk)1×h.

在一般的等级评价问题中,最大隶属度原则是一种比较常用的规则,即根据等级隶属度utk的大小,对城镇污水处理厂At做出清洁生产等级评定.不过,最大隶属度原则有时会出现一些不合理的现象.为此,本文将在下面小节中引入级别特征值概念,并结合二元语义概念[13,19],提出城镇污水处理厂清洁生产等级评价二元语义方法.

4.2 清洁生产等级评价二元语义方法

把清洁生产等级ek的下标k称为级别变量.于是,可把城镇污水处理厂At的级别特征值定义为:

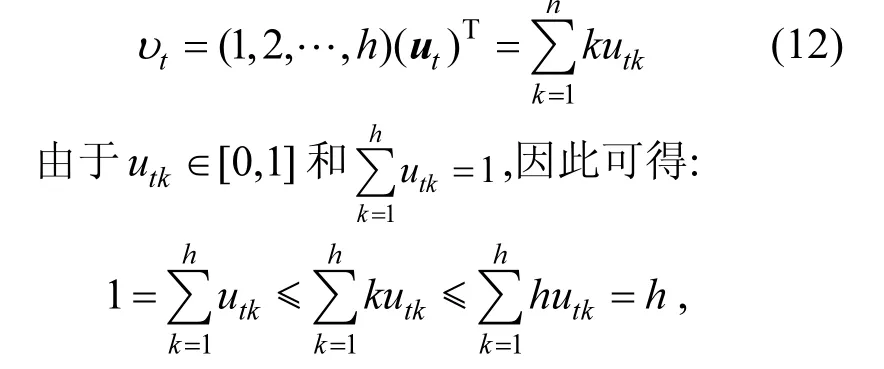
则由式(12)可知,污水处理厂At的级别特征值υt是1个无量纲的数量指标,介于清洁生产第1个等级(即e1)与第h个等级(即eh)之间,反映了清洁生产等级评价综合隶属度与清洁生产等级(即级别位置)2个方面的重要信息.

用记号[υt]表示不大于υt的最大整数.通常地,若[υt]=q,则可以评定污水处理厂At属于清洁生产的第q个等级(即eq).一般地,采用级别特征值υt取最大整数方法评定污水处理厂清洁生产等级要比利用最大隶属度原则更加全面和客观.然而,仔细分析可以发现,不同的级别特征值可能会取相同的一个最大整数.例如,级别特征值υ1=2.03和υ2=2.97的最大整数都是2,对应的污水处理厂A1和A2都应评定为清洁生产等级e2.但是,很显然,A1和A2不应属于清洁生产的同一等级.直观上,A1和A2分别评定为清洁生产等级e2、e3要更合理、准确.同样,级别特征值υ3=2.01和υ4=1.99的最大整数分别是2和1,对应的污水处理厂A3和A4应分别评定为清洁生产等级e2和e1.不过, υ3=2.01和υ4=1.99的差异很小且均接近于2,其对应的污水处理厂却被评定为不同的清洁生产等级,显然是不合理的.直观上, υ4对应的污水处理厂A4也应评定为清洁生产等级e2.上述两方面的分析表明,采用级别特征值取最大整数方法虽然比利用最大隶属度原则可以更好地反映污水处理厂清洁生产等级综合情况,但也会出现一些不合理现象,导致错误评定其清洁生产等级或无法清楚区分污水处理厂之间清洁生产的差异程度[20].

为了既能正确地评定城镇污水处理厂清洁生产等级,又能准确地反映相同清洁生产等级下各个污水处理厂清洁生产的差异程度,本文引入下面的二元语义概念[12,18],并据此建立污水处理厂清洁生产等级评价二元语义方法.

若污水处理厂At的级别特征值υt满足:

则评定At的清洁生产等级为第s个等级(即es).

为了刻画属于相同清洁生产等级的不同污水处理厂清洁生产的差异程度,把级别特征值υt与其相应的清洁生产级别s(即等级es的下标s)之间的偏差值表示为αts=υt−s ,如图3所示.显然,−0.5≤αts<0.5.

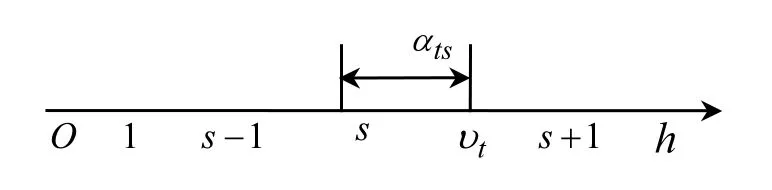
图3 二元语义与级别特征值关系Fig.3 Relation between two-tuple semantic and grade eigenvalue

城镇污水处理厂清洁生产等级评价二元语义方法的基本思想是:首先,把污水处理厂At的级别特征值υt表示为二元有序组(es, αts),其中es为清洁生产等级和αts∈[−0.5,0.5);其次,按照(es, αts)中的es大小,评定污水处理厂At的清洁生产等级;然后,根据(es, αts)中的αts大小,调整、确定污水处理厂At清洁生产的差异程度(即确定相同清洁生产等级的污水处理厂的优先排序).

显然,αts在清洁生产等级评定中起到一种调整的信号作用,反映清洁生产级别s比υt大还是小.因此,常称(es, αts)为二元语义,而称αts为语义符号.

为了使污水处理厂清洁生产等级评价二元语义方法便于操作与计算机实现,规定二元语义的大小如下:

(1)若es>ed(即s(ed,αrd),即污水处理厂At的清洁生产等级高于Ar,其中(es, αts)、(ed, αrd)分别是污水处理厂At、Ar的级别特征值υt和υr对应的二元语义;

(2)若es=ed(即s=d),则污水处理厂At与Ar的清洁生产等级相同,这时可根据语义符号调整、确定它们的差异程度,具体做法:①当αts=αrd时,有(es,αts)=(ed,αrd),即At与Ar的清洁生产程度完全一样;②当αts>αrd时,有(es,αts)<(ed,αrd),即At的清洁生产程度比Ar差(尽管都属于相同的清洁生产等级),或者说,At的优劣排序在Ar之后;③当αts<αrd时,有(es,αts)>(ed,αrd),即At的清洁生产程度比Ar好,也即At的优劣排序在Ar之前.

显然,这样规定的二元语义排序方法既可以评定污水处理厂的清洁生产等级,又能区分相同清洁生产等级的污水处理厂清洁生产的差异程度.

5 城镇污水处理厂清洁生产等级评价实例分析

选取大连市3家污水处理厂A1、A2和A3作为清洁生产等级评价对象.污水处理厂A1建于1997年,采用A/O处理工艺,出水达到《城镇污水处理厂污染物排放标准》(GB18918-2002)[21]中二级标准后排海.污水处理厂A2建于2007年,系国家863项目“水环境质量改善技术与综合示范”的重点示范工程之一,采用水解池+DN生物滤池+CN生物滤池的SBR处理工艺,出水达到一级B标准[21]后全部作为景观水回用.污水处理厂A3建于2006年,采用水解池+DN生物滤池+CN生物滤池的处理工艺,出水达到一级B[21]标准后一部分回用、剩余部分排海.通过实际测量、获取在线监测数据与实地调查等方法,得到3家污水处理厂实际的清洁生产评价指标值,见表2.

根据式(1)～式(8)和表2,可计算得到污水处理厂A1关于二、三级评价指标的等级隶属度矩阵,以µ11和µ131为例,结果如下:

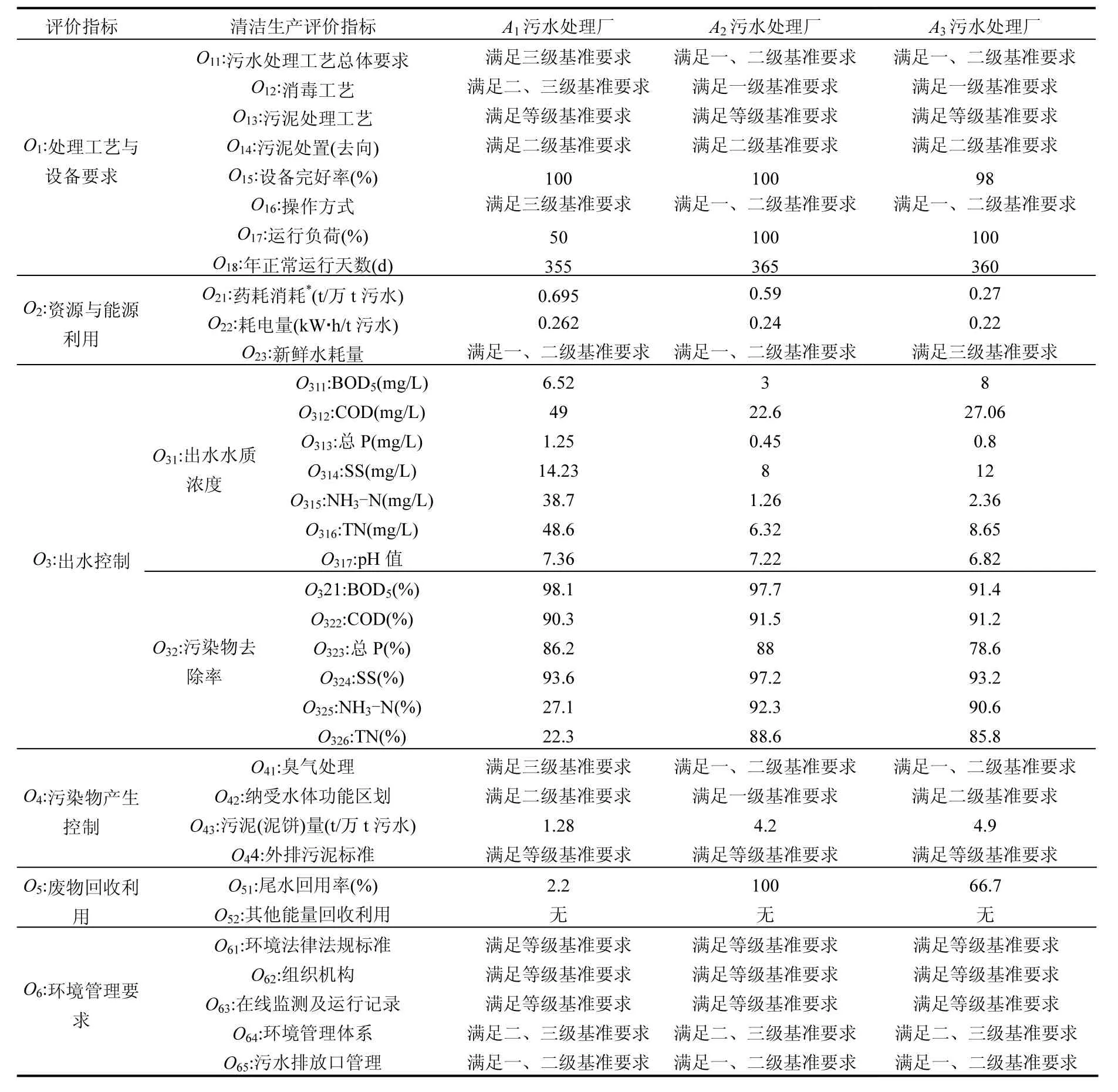
表2 三家污水处理厂各清洁生产评价指标值Table 2 Evaluation index values of cleaner production of three town sewage treatment plants

利用式(9),并结合表2的评价指标权重,可算得污水处理厂A1关于二级评价指标O31对于清洁生产等级e1、e2、e3的综合隶属度分别为:u1311=0.276,u1312=0.366,u1313=0.358,从而可得A1关于O31的等级综合隶属度向量为u131=(0.276,0.365,0.358).

类似地,可得到污水处理厂A1关于二级评价指标O32对于清洁生产等级e1、e2、e3的综合隶属度分别为:u1321=0.344,u1322=0.327,u1323=0.329,也即得到A1关于O32的等级综合隶属度向量u132=(0.344,0.327,0.329).

于是,得到了污水处理厂A1关于一级评价指标O3下所有二级评价指标的等级隶属度矩阵为:

利用式(10)和表1的评价指标权重,可计算得到污水处理厂A1关于一级评价指标O3对于清洁生产等级e1、e2、e3的综合隶属度分别为:u131=0.31,u132=0.35,u133=0.34,即得到A1关于O3的等级综合隶属度向量u13=(0.31,0.35,0.34).

类似地,可计算得到污水处理厂A1关于一级评价指标Oi(i=1,2,4,5,6)的等级综合隶属度向量分别为:u11=(0.19,0.35,0.46),u12=(0.34,0.39, 0.27),u13=(0.31,0.35,0.34),u14=(0.26,0.32,0.42), u15=(0.02,0.18,0.80),u16=(0.31,0.38,0.31).于是,得到了A1关于一级评价指标的等级隶属度矩阵为:

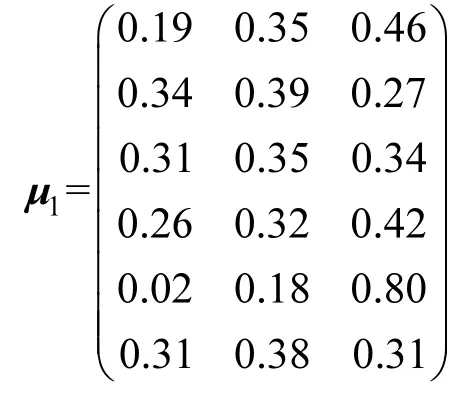
利用式(11)和表1的指标权重,计算得到A1对于清洁生产等级e1、e2、e3的综合隶属度分别为:u11=0.26,u12=0.33,u13=0.41,即得到了A1的等级综合隶属度向量u1=(0.26,0.33,0.41).同样可计算得到u2=(0.40,0.36,0.24),u3=(0.35, 0.38,0.27).

利用式(12),计算得到A1的级别特征值为: υ=(1,2,3)uT=(1,2,3)(0.26,0.33,0.41)T=2.15.

类似地,可计算得到A2和A3的级别特征值分别为:υ2=1.84,υ3=1.92.

根据式(13),可把污水处理厂A1、A2和A3的级别特征值分别表示为下面的二元语义:

υ1=(2,0.15),υ2=(2,−0.16),υ3=(2,−0.08).按照前面规定的二元语义大小关系,可评定污水处理厂A1、A2和A3的清洁生产等级均为e2(即国内清洁生产先进水平),但它们清洁生产程度不是完全一样的,其优劣排序为:A2>A3>A1,即A2比较好、A3居中、A1比较差.

从上述3个污水处理厂的各单项指标对比来看,污水处理厂A2各项指标值总体上要明显好于A1和A3,而A1的各单项指标值相对来说是最差的.计算得到的排序结果与单项指标的对比情况相一致,但通过计算得出的结论显得更严谨、更可靠、更直观.

若采用最大隶属度原则,则污水处理厂A1、A2和A3的清洁生产等级可分别评定为:A1属于等级e3;A2属于等级e1;A3属于等级e2.然而,A2属于等级e1和属于等级e2的隶属度相差不多,且属于等级e2、e3的隶属度之和大于其属于等级e1的隶属度,即:u22+u23=0.36+0.24=0.60>0.40=u21.因此,把污水处理厂A2的清洁生产等级评定为等级e1是不合适的,应该评定为等级e2,这样才会更加符合A2的清洁生产实际情况.类似地,把污水处理厂A1的清洁生产等级评定为e3也是不合理.究其原因在于最大隶属度原则仅仅考虑等级隶属度的相对大小,而忽略了各个清洁生产等级的位置差异.

若采用对级别特征值取最大整数方法,由于[υ1]=2、[υ2]=1和[υ3]=1,则可评定污水处理厂A2和A3的清洁生产等级均为e1、A1的清洁生产等级为e2.分析发现,级别特征值υ1=2.15和υ3=1.92比较接近2,且相差并不大,但对应的污水处理厂却被评定为不同的清洁生产等级,这是不合理的.直观上,由于υ3与2很接近,应把A3的清洁生产等级评定为e2.这表明,采用对级别特征值取最大整数方法评定污水处理厂清洁生产等级也会出现一些与利用最大隶属度原则一样的不合理现象.

6 结语

构建了城镇污水处理厂清洁生产等级评价递阶指标体系及其定性与定量评价指标的等级隶属函数,据此建立了污水处理厂清洁生产等级评价模糊综合模型,进而提出城镇污水处理厂清洁生产等级评价二元语义方法.理论分析与实例计算分析表明,本文提出的污水处理厂清洁生产等级评价二元语义方法不仅符合等级评价的概念要求,而且是可行、有效的,具有更好的适用性,并便于计算机进行符号运算与处理,可为解决清洁生产等级评价问题提供一条新途径,也可推广应用于类似的等级评价问题.

[1] Almeida C M V B, Bonilla S H, Giannetti B F, et al. Cleaner Production initiatives and challenges for a sustainable world: an introduction to this special volume [J]. Journal of Cleaner Production, 2013,47:1-10.

[2] 李 芳.清洁生产在污水处理厂中的应用思考 [J]. 科技创业家, 2012(8):206-206.

[3] 马乐宽,王金南,王 东.国家水污染防治“十二五”战略与政策框架 [J]. 中国环境科学, 2013,33(2):377-383.

[4] 尹发平.城镇污水处理厂清洁生产措施分析 [J]. 广东化工, 2012,39(16):131-132.

[5] 叶 微,魏立安.用模糊评价法确定清洁生产审核重点之探讨[J]. 江西科学, 2008,26(2):324-327.

[6] 刘志鹏,毕俊生,寻翠翠.德国推行清洁生产经验及对我国的启示 [J]. 环境科学导刊, 2012,31(2):24-25.

[7] Crouse B A, Ghoshdastidar A J, Tong A Z. The presence of acidic and neutral drugs in treated sewage effluents and receiving waters in the Cornwallis and Annapolis River watersheds and the Mill Cove Sewage Treatment Plant in Nova Scotia, Canada [J]. Environmental Research, 2012,112:92-99.

[8] Cai Q Y, Mo C H, Wu Q T, et al. Occurrence of organic contaminants in sewage sludges from eleven wastewater treatment plants, China [J]. Chemosphere, 2007,68(9):1751-1762.

[9] Wang C, Hu X, Chen M L, et al. Total concentrations and fractions of Cd, Cr, Pb, Cu, Ni and Zn in sewage sludge from municipal and industrial wastewater treatment plants [J]. Journal of Hazardous Materials, 2005,119(1-3):245-249.

[10] Berker R V. Cleaner production and eco-efficiency initiatives in Western Australia 1996-2004 [J]. Journal of Cleaner Production, 2007,15(8/9):741-755.

[11] 顾文权,邵东国,黄显峰,等.模糊多目标水质管理模型求解及实例验证 [J]. 中国环境科学, 2008,28(3):284-288.

[12] Li D F. Decision and game theory in management with intuitionistic fuzzy sets [M]. Springer-Verlag, Heidelberg, Germany, 2014.

[13] Herrera F, Herrera-Viedma E. Linguistic decision analysis: steps for solving decision problems under linguistic information [J]. Fuzzy Sets and Systems, 2000,115(1):67-82.

[14] 孙迎雪,吴光学,胡洪营.基于达标保证率的昆明市污水处理厂出水水质评价 [J]. 中国环境科学, 2013,33(6):1113-1119.

[15] 陈文立,蒋伟萍.污水处理厂清洁生产评价指标体系的构建 [J].环境保护与循环经济, 2013,7:28-30.

[16] 中华人民共和国环境保护部.清洁生产评价指标体系编制通则[S]. 北京, 2013.6.

[17] Monia1N, Massimo P, Gundorph B H, et al. Comparative life cycle assessment of wastewater treatment in Denmark including sensitivity and uncertainty analysis [J]. Journal of Cleaner Production, 2014,68:25-35.

[18] Wang W J, Zhou X D, Wu J. Research on the cleaner production of municipal waste water treatment plants in Zhejiang Province. International Conference on Electric Information and Control Engineering, 2011 [C]. NJ, USA, IEEE, 2011:15-17.

[19] Herrera F, Herrera-Viedma E, Martínez L. A fuzzy linguistic methodology to deal with unbalanced linguistic term sets [J]. IEEE Transactions on Fuzzy Systems, 2008,16(2):354−370.

[20] Li D F. Multiattribute group decision making method using extended linguistic variables [J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2009, 17(6):793-806.

[21] GB18918-2002 城镇污水处理厂污染物排放标准 [S].

Two-tuple semantic model and method of cleaner production grade evaluation for town sewage treatment plants.

WANG Li-ling, ZHANG Shu-shen*, ZHANG Yun (Key Laboratory of Industrial Ecology and Environmental Engineering, Ministry of Education, School of Environmental Science and Technology, Dalian University of Technology, Dalian 116024, China). China Environmental Science, 2014,34(11)：2976～2984

The cleaner production grade evaluation problem of wastewater treatment plants was studied through the method of combining qualitative analysis with quantitive computation. The index system of cleaner production grade evaluation for urban sewage treatment plants and corresponding weights’ determination method were proposed. The fuzzy comprehensive model of the cleaner production grade evaluation for town sewage treatment plants was established and the two-tuple semantic model and method through introducing the concept of the grade eigenvalue were developed through using the linear weighted comprehensive method, fuzzy mathematics and the concept of two-tuple semantic. It was illustrated with a real example that the established two-tuple semantic model and method of the cleaner production grade evaluation were more operational, intuitionistic and easily explained. Thus, the two-tuple semantic model and method proposed in this paper were of good applicability and generalization value.

sewage treatment；cleaner production；fuzzy comprehensive model；two-tuple semantic；grade evaluation

X32

A

1000-6923(2014)11-2976-09

王丽玲(1978-),女,辽宁大连人,工程师,博士,主要从事工业生态与环境规划方面的研究.发表论文5篇.

2014-02-13

国家自然科学基金项目(71231003,71171055)

* 责任作者, 教授, zhangss@dlut.edu.cn