湖库富营养化的改进型模糊综合评价方法研究

陈藜藜,金腊华*(1.暨南大学环境学院,广东 广州 510632；2.广东省高校水土环境毒害性污染物防治与生物修复重点实验室,广东 广州 510632)

湖库富营养化的改进型模糊综合评价方法研究

陈藜藜1,2,金腊华1,2*(1.暨南大学环境学院,广东 广州 510632；2.广东省高校水土环境毒害性污染物防治与生物修复重点实验室,广东 广州 510632)

针对水体富营养化评价系统的非线性、模糊综合评价法过程中权重赋予的主观随意性和隶属函数的不准确性等特点,对传统模糊综合评价法进行了改进,并据此对我国24个代表性湖库的富营养化程度进行了评价.其中以SPSS16.0和Yaaph软件为载体,采用层次分析法和主成分分析法相结合来确定选取因子的权重.根据确定的评价标准作自然对数变换使之线性化,并结合由基础数据统计分布情况,生成各评价因子隶属于各营养等级的对数形式的降半梯形隶属函数,进而得到各湖库的确定度,最后依据最大确定度得到湖库富营养化级别.该法所得结果与湖库实际富营养化状况以及现有多种评价方法的结果的对比表明,该改进方法的评价结果真实、准确、计算简单,具有可行性.

富营养化；改进型模糊综合评价；层次分析法(AHP)；主成分分析法(PCA)

科学合理地评价水体富营养化程度,对湖库水质保护具有十分重要的意义.目前,国内外学者提出的水体富营要养化评价方法主要有卡尔森营养状态指数[1]、营养状态指数法[2-6]、生物指标评价法[7]、主成分分析法[8-9]、灰色评价[10]、神经网络法[11-12]、基于云模型[13]、基于延拓盲数[14]的水体富营养化评价法和模糊综合评价法[15-16]等.虽然研究方法种类较多,但由于水体富营养化评价体系的非线性特征,富营养化等级之间关系模糊[17],且这些采用的方法均有与其相适应的条件,具有一定的局限性,同时与之所采用的分级标准和评价指标也不统一,缺乏通用性,因此至今尚未形成一种统一的评价模型.尽管这些评价方法都在我国水体中已有应用,但是对我国大部分水体的适应性还有待研究.

模糊综合评价法以美国学者 Zadeh[18]提出的模糊数学理论为基础,是目前水体富营养化评价最为广泛的评价方法之一,其产生的结果以向量的形式出现,可提供更为丰富的评价信息;模糊综合评价方法的适用广泛,算法人为可操作性强,可行性大,可用于主客观因素的综合评价,又可用于客观因素的综合评价[19-21];但评价过程中权重的确定不是伴随评价过程产生的,而是人为确定,主观性太大,并且针对评价系统非线性问题,隶属函数的确定缺乏客观准确性,以至于没法精确地达到评价要求.

为此,本文在传统模糊综合评价模型基础上,采用层次分析和主成分分析结合来确定评价指标权重,隶属函数结合评价标准界限值进行对数变换而确定,并以我国24个主要湖库的富营养化程度评价实例验证该方法的可行性和有效性.

1 模糊综合评价法的改进

在传统模糊综合评价法的基础上,针对其存在的缺点进行改进,具体步骤如下:

第一,确定权重.将主观与客观结合,以SPSS16.0和yaahp软件为载体,采用定性的层次分析法和定量的主成分分析法结合来确定评价因子权重,使权重的确定更为客观.

第二,构建隶属函数.针对评价标准的等级界限非线性特征和由客观基础数据统计得出的降半梯形分布,并为了使得评价结果能在线性等级中准确表达所隶属的富营养化程度,本文对客观基础数据进行统计并结合确定的评价标准作线性变换,来构建对数形式的降半梯形隶属函数.

第三,综合评价.由构建的隶属函数得出各营养级别的隶属度,再根据隶属度最大原则确定评价对象最终富营养化等级.

2 基于改进型模糊综合评价的水体富营养化程度评价方法

2.1 评价指标及其权重的确定

根据《地表水环境质量评价办法(试行)》[22]中的相关规定,湖库营养状态评价指标为:叶绿素a(Chl-a)、总磷(TP)、总氮(TN)、透明度(SD)和高锰酸盐指数(CODMn)共 5项.由于湖库富营养化评价影响因素众多而难以客观量化,难以反映实际情况.针对此情况,本文以yaahp和SPSS16.0软件为辅助方式,采用定性与定量结合对这 5项指标进行权重赋值.具体如下:

(1) 层次分析法定性确定权重

用层次分析法对 5个因子进行两两比较,且在构成判断矩阵时采用五标度数值判别法.根据相关文献研究成果[23-26]以及水体实际情况可知,对于水体富营养化而言,Chl-a因子最重要,其直接反映藻类现存量的指标,其次是藻类增殖的主要限制因子 TN、TP;然后是其他两因子.据此应用(1,3,5,7,9)五标度数值判别法构造各因子的判断矩阵 A={aij},具体重要排序为:Chla>TN>TP> SD>CODMn.运用 yaahp软件得出层次分析法权重WAi.

(2) 主成分分析法确定权重

主成分分析法是一种在确保系统原有数据信息量丢失最小的原则下,在各个变量相关关系研究的基础上,将多个变量的信息压缩为几个能反映原问题特征的综合变量指标,并据此特征信息指标对系统进行综合分析的比较完善的多元统计分析方法.因此,它能避免人为确定各指标权重的主观随意性,在进行水体富营养化评价能取得客观定量化的评价效果[9,27].

根据主成分分析法的原理,利用 SPSS软件进行主成分分析既避免了运算的复杂性,也提高了计算的精确性,具体步骤为:①首先根据收集的指标基础数据计算KMO以及Bartlett球度检验给出的相伴性概率,判断指标数据是否适合进行主成分分析,若KMO>0.60且相伴性概率小于显著性水平0.05,则认为基础数据适合主成分分析;②经过正交旋转后;得到各因子变量在许多变量上的载荷数;③对因子载荷矩阵旋转后的结果表进行公因子方差求和,然后将各指标公因子方差与所有指标的公因子方差和相除,即得到各指标的权重值WZi.

(3) 运用主客观综合赋权法[28]确定指标权系数 α*,β*.根据 w=α*w+β*w,确定评价指标

i AiZi综合权重wi.

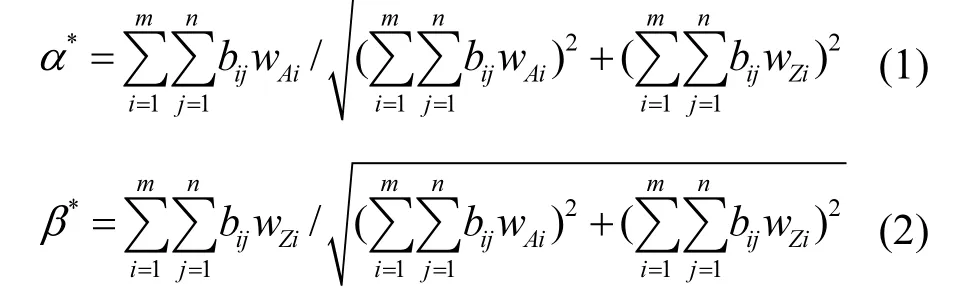
式中:bij为评价指标标准化数值,α＊和 β*分别为层次分析法和主成分分析法权重的重要程度.

2.2 评价等级划分

本文在参考大量文献和结合实测数据具体分布特点的基础上,以金相灿的《湖泊富营养化调查规范》[29]中富营养化状态指标与水质参数关系表的数值为依据,采用金相灿等提出的评价标准,具体评价标准见表1.通过分析发现对标准分级值进行对数变换后,基本符合线性规律,见图1.

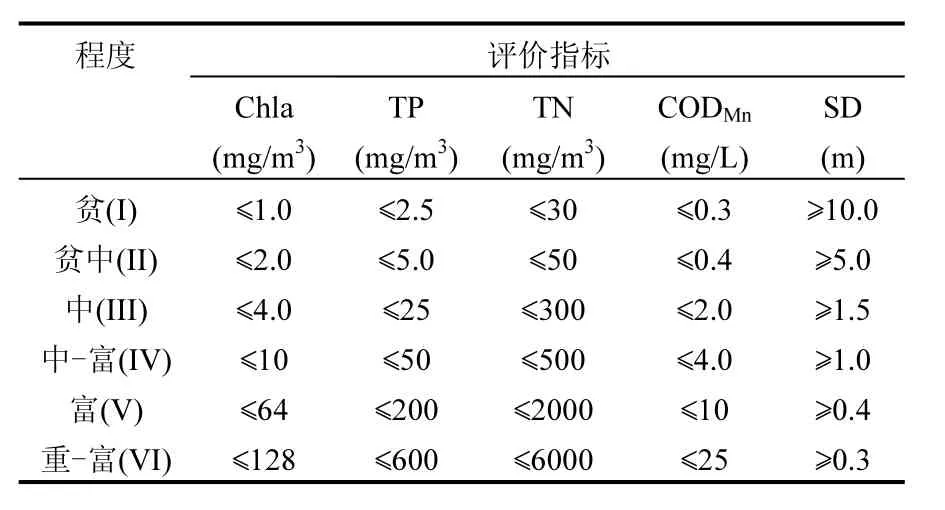
表1 我国湖库富营养化评价标准Table 1 Classification standard of eutrophication status in lakes or reservoirs

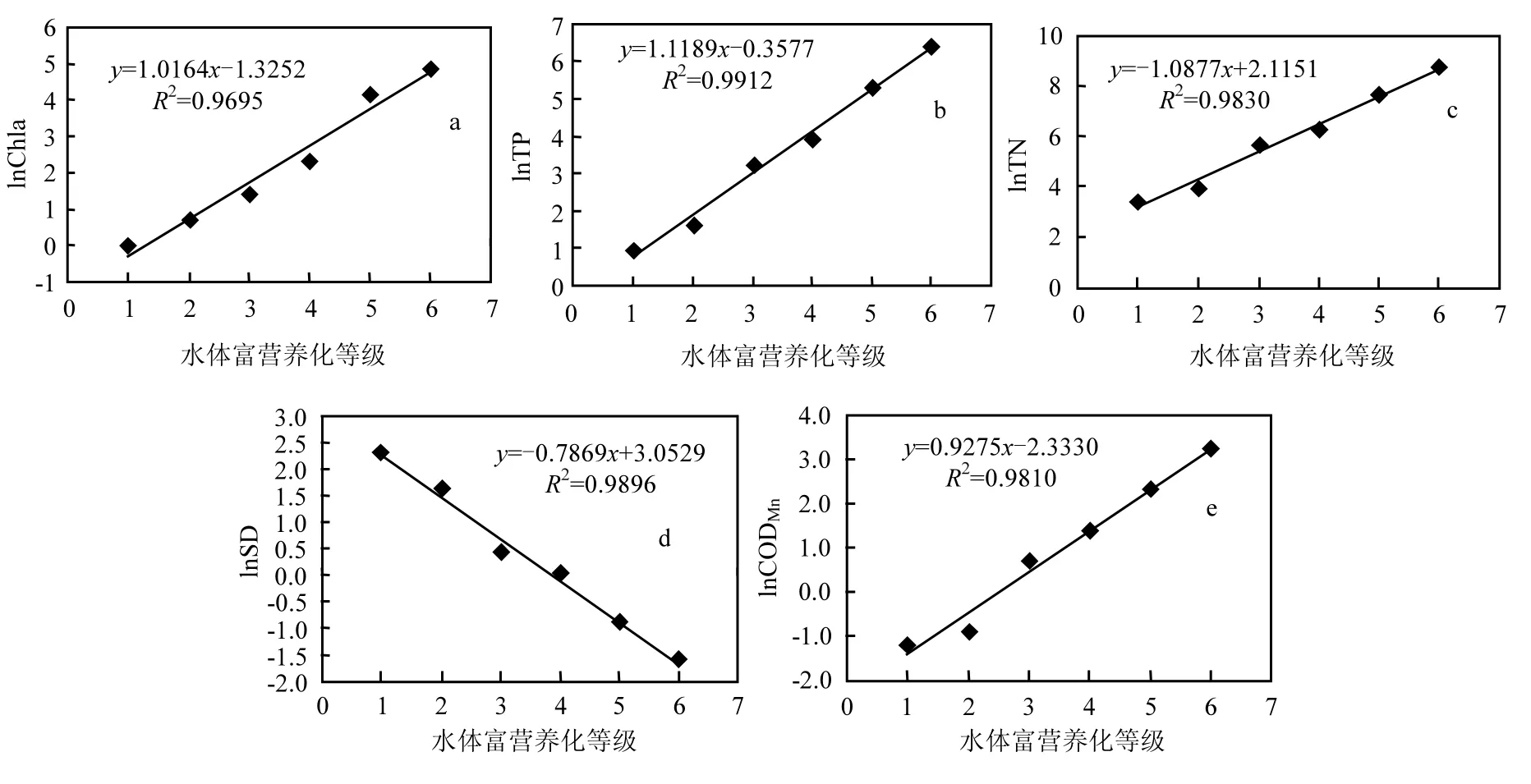
图1 对数变换后的水体富营养化评价标准界值分布Fig.1 Distribution of boundary values of eutrophication evaluation criteria after logarithmic transformation

2.3 建立隶属函数

通过基础数据统计分析,描述出大致的曲线,将它与 Fuzzy六种分布图[30]作比较,选择出最接近的一个分布形式---降半梯形分布,并结合评价体系非线性特征以及评价标准构建出模糊综合评价水体富营养化程度的隶属函数.对于Chla、TP、TN、CODMn4个因子是实测值越大,富营养化程度越高,称之为正指标;SD是实测值越大,富营养化等级越低,称之为负指标.各正指标(除SD外)对于水体富营养化每一级的隶属函数如下:式中: r为隶属函数, χi为各评价因子的实测值,下标i为某评价因子,i=1,2,…5;k≥3;对于正指标,Sij为评价等级标准对应区间的上限值,对于负指标,Sij为评价等级标准对应区间的下限值.对于负指标 SD,其基本表达式不变,只需要改变条件中的符号方向.

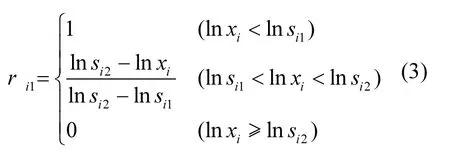
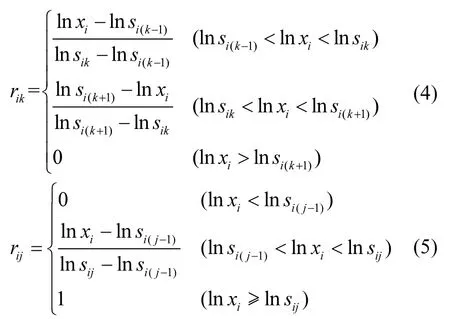
根据每个评价水体5个因子的实测值、评价等级标准以及隶属函数建立评判矩阵 R={rij}, (i = 1,2,⋅ ⋅⋅,5; j= k ,⋅ ⋅⋅,6).

2.4 评价矩阵的复合运算及综合评价

在建立评判矩阵 R和得到各个因子的权重wi后,将 R与 W 进行评判矩阵的符合运算B =W⋅ R,采用加权平均算子模型,其计算公式为:bj=∑( wi⋅ rij) ,通过计算得出模糊综合评价的结果向量(隶属矩阵).

根据模糊综合评价得到的隶属矩阵按照最大隶属度原则,得出最终评判等级.

3 实例应用与验证

3.1 评价指标及其权重的确定

根据上述改进型模糊综合评价方法,结合我国主要24个湖库1987～1989年的水体营养化调查资料[29]进行实例验证方法的可行性.

3.1.1 确定权重 (1)运用层次分析法构建判断矩阵,通过yaahp软件计算得出Chla、TP、TN、SD 和 CODMn的权重(WAi)的向量 Ai=(0.2785, 0.2341,0.2334,0.1608,0.0931),并一致性检验均满足CR≤0.1的要求. (2)通过SPSS软件进行主成分分析.根据收集 24个湖库的基础数据[29]计算出KMO为0.833,根据统计学家Kaiser给出的评判标准可知,KMO>0.6且Bartlet球度检验得出的相伴性概率为 0.000,小于显著性水平 0.05,即拒绝Bartlet球度检验零假设,则认为24个湖库的基础数据适合于主成分分析并运行结果可行.通过正交旋转和公因子方差法计算,得评价指标 Chla、TP、TN、SD、CODMn权重值(WZi)向量为Zi=(0.2161,0.1963,0.1692,0.2314,0.1871). (3)得出综合权重值.根据(1)～(2)计算得到两种权重方法的重要程度,并由 wi=α*wAi+β*wZi计算得出Chla、TP、TN、SD、CODMn的权重向量 Wi= (0.2473,0.2152,0.2013,0.1961,0.1401).

3.1.2 建立隶属函数 确定各因子于各营养等级的隶属度.根据构建的隶属函数(3)～(5),代入评价标准界值和基础数据,分别得到每种评价因子相应于不同级别的隶属函数.例如:叶绿素a(Chl-a)的隶属函数如下.同样,可以得到TP、TN、SD、CODMn对于各个营养等级的隶属函数.

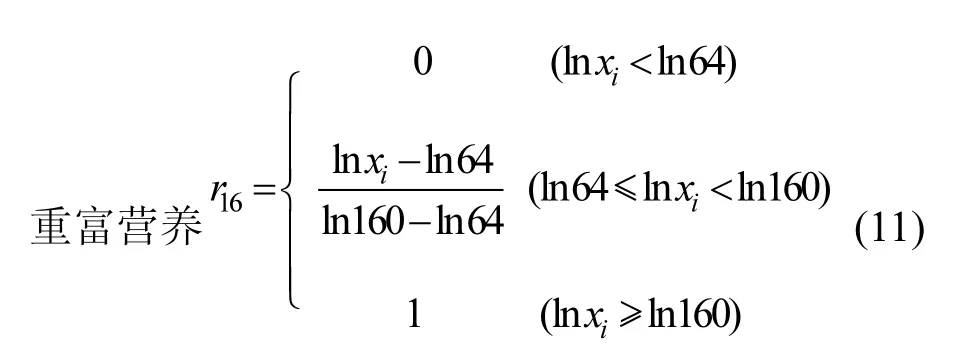
3.1.3 评价因子与等级之间模糊关系的构建 将24个湖库实测数据(表2)一一代入各个具体的隶属函数中(如叶绿素a的实测数据代入式

(6)～式(11)中),可计算出每个湖库的评判矩阵R.

3.1.4 进行矩阵复合运算 采用加权平均算B= W⋅ R,其计算公式为 bj=∑(wi⋅ rij),得出模糊综合评价的结果向量,即隶属度矩阵 B=(b1,b2,b3, b4,b5,b6),并按照隶属度最大原则得到综合评价结果,见表2.

3.2 方法验证

为了证实结果的有效性,针对同样的数据资料,本文采用的模型方法评价结果与国内外应用较为广泛的评分指数法(1993年)[12,31]以及近年来一些新的评价方法所得结论进行了比较,具体包括有3种神经网络模型(2006～2007年)[13,33]、投影寻踪模式评价(2009年)[12,32]、云模型(2013年)[13],最终各方法的详细结果见表2.

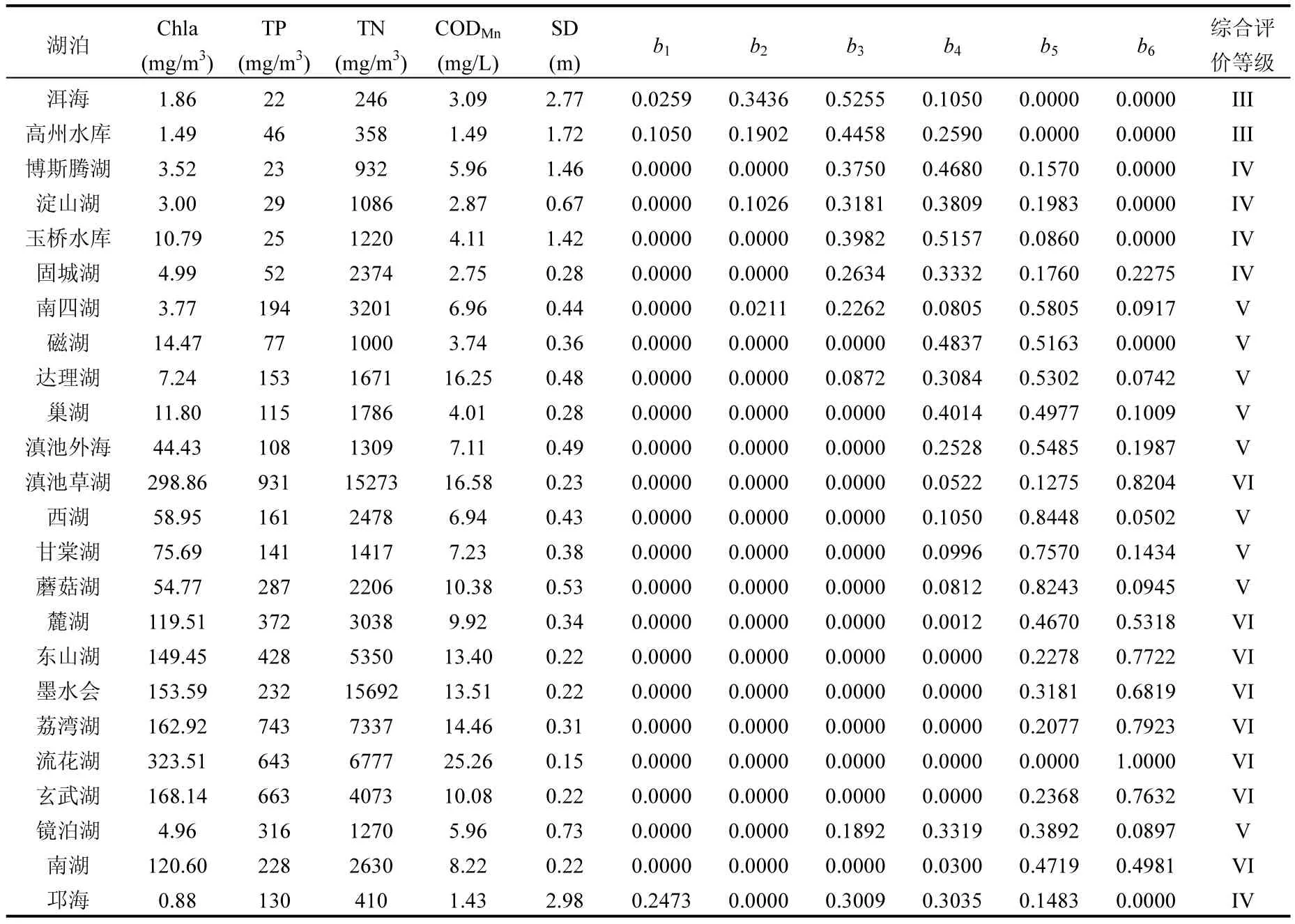
表2 我国24个主要湖泊1987～1989年富营养化调查数据及评价结果Table 2 Investigated data and evaluation results of 24 lakes and reservoirs in China during 1987～1989

3.3 结果及讨论

根据表 3各种方法的结果比较,改进型模糊综合评价与参照方法评价结果基本一致,除博斯腾湖、滇池草湖和邛海在各方法取得的结果相差一个等级外,其他湖库评价等级结果完全一致,证明了方法的可行性和准确性.

将表 2的分级结果与湖库水体实际情况相比照,例如滇池草湖,沈晓飞等指出调查表明自20世纪80年代以来滇池草湖水体Chla浓度严重超标,水华严重,水体富营养化异常严重,且草湖污染程度远较外海严重[34].根据本文评价方法草湖被定为 VI级,即重富营养化,与真实情况相符合;与各湖库用水障碍实际情况对照,例如,邛海和博斯腾湖在实际中都没有发现有用水障碍情况,被定为 IV级是合理有效的,同时从各级别的隶属度可以看出,博斯腾湖和邛海对III、IV级的隶属度分别为0.3750、0.4680和0.3009、0.3035,可以直观地看出两者都处于III、IV级之间,即中-中富营养级,只是更接近中富营养级,同时也表明博斯腾湖较邛海富营养化程度重.由此可见,水体富营养化的改进型模糊综合评价法能全面地反映同级别水体富营养化程度的高低,且更为准确地贴实际情况.

由于模糊综合评价法本身的特性,将其用于水体富营养化程度评价能够充分体现分级评价系统中的模糊性和随机性,而改进后的模糊综合评价又能较精确地确定各个评价因子的权重.依照监测点各评价因子的实测数值,可以直观地对水体营养化程度进行分析.以邛海为例,评价因子Chla浓度较小,根据标准,处于I级;TP浓度偏高,则处于V级;评价因子TN的浓度,处于IV级;而透明度SD处于III级.各种评价因子分别处在4个不同的级别上,无法主观直接判断该监测点的富营养化级别,但是根据各评价因子的权重,Chla权重最大,TP次之,至少可以很直观判断出很大程度上不会属于第V营养级,再运用改进型模糊综合评价法,可以直观地将其定位于营养化级别IV级,与实际用水状况及参照方法分级结果相符.

本文对湖库水体富营养化等级的划分是参考大量文献基础上,结合1987～1989年24个湖库调查资料,以及考虑目前湖库水体富营养化程度的实际情况而采用金相灿学者提出的分级标准,目的是为了更好的建立能准确分析湖库水体营养等级的评价模型.

本研究结合评价标准和实测数据分布的具体特点来设计隶属函数,并结合基础数据的降半梯形分布特点,构建对数形式的降半梯形隶属函数,从而避免了仅从单纯的评价标准或者基础数据分布特点考虑而构建,可能造成评价结果与实际情况存在较大偏差的情况;同时,在权重方面,主客观结合,增加了权重确定的客观性、合理性,使得评价结果更合理、贴近实际情况.

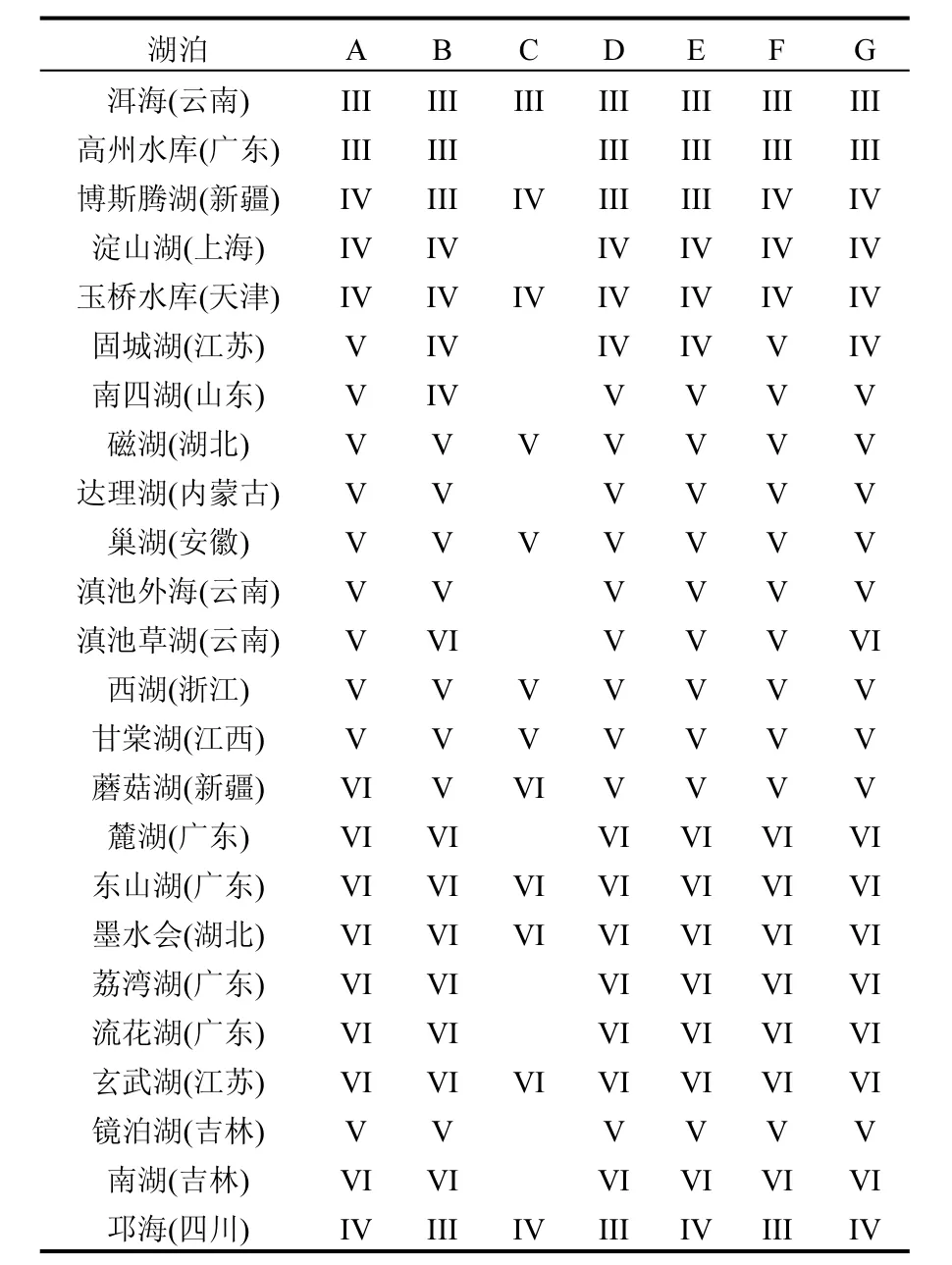
表3 不同方法对各湖库富营养化程度评价结果比较Table 3 Comparison of evaluation results by different methods

4 结论

4.1 针对传统模糊综合评价在水体富营养化评价中权重确定主观性大的不足和评价系统的非线性、隶属函数不准确的特点,将层次分析法与主成分分析法结合确定评价指标权重,对评价等级标准界值作自然对数变换后,将其与隶属函数相结合,构建了改进型的模糊综合评价模型.运用24个湖库水质实测资料对方法进行了验证,结果表明,改进后的模糊综合评价能够真实反映湖库水体富营养化程度.

4.2 改进的方法是针对一般水体的富营养化问题和普遍的评价方法存在的问题而提出的,具有普适性;同时评价方法具有原理简单,操作简易的优点,为湖库富营养化状况评价提供了一个更为简便、有效且普遍适应的方法,对湖库水体富营养化评价具有一定的指导意义.

[1] Yang J, Yu X Q, Liu L M, et al. Algae community and trophic state of subtropical reservoirs in southeast Fujian, China [J]. Environmental Science and Pollution Research, 2012,19(5):1432-1442.

[2] 张华俊,李秋华,韩博平.南亚热带典型调水型水库-广东大镜山水库的富营养化特征分析 [J]. 湖泊科学, 2010,22(2):291-299. [3] 许秋瑾,郑丙辉,朱延忠,等.三峡水库支流营养状态评价方法[J]. 中国环境科学, 2010,30(4):453-457.

[4] 单保庆,菅宇翔,唐文忠,等.北运河下游典型河网区水体中氮磷分布与富营养化评价 [J]. 环境科学, 2012, 33(2):352-358.

[5] 李如忠,刘科峰,钱 清,等.合肥市区典型景观水体氮磷污染特征及富营养化评价 [J]. 环境科学, 2014,35(5):1718-1726.

[6] 曾庆飞,谷孝鸿,毛志刚,等.固城湖及上下游河道富营养化和浮游藻类现状 [J]. 中国环境科学, 2012,32(8):1487-1494.

[7] 王 旭.白洋淀富营养化评价与数值模拟研究 [D]. 大连:大连理工大学, 2008.

[8] Cai Q H, Liu J K, Lorenz K. A comprehensive model for assessing lake eutrophication [J]. Chinese Journal of applied ecology, 2002,13(2):1674-1678.

[9] 张维砚,沈蓓雷,童 琰,等.基于GA-BP模型的景观小水体富营养化评价方法 [J]. 中国环境科学, 2011,31(4):674-679.

[10] 胡丽慧,潘 安,李铁松,等.灰色聚类法在升钟水库水体富营养化评价中的应用 [J]. 农业环境科学学报, 2008,27(6):2407-2412.

[11] 邓大鹏,刘 刚,李学德,等.基于神经网络简单集成的湖库富营养化综合评价模型 [J]. 生态学报, 2007,27(2):725-731.

[12] 崔东文.MATLAB神经网络在湖库富营养化程度评价中的应用-以全国24个湖泊富营养化程度评价为例 [J]. 环境研究与监测, 2006,26:42-48.

[13] 丁 昊,王 栋.基于云模型的水体富营养化程度评价方法 [J].环境科学学报, 2013,33(1):251-257.

[14] 尹 星,李如忠,杨继伟,等.基于延拓盲数的湖库水体富营养化评价模型 [J]. 环境科学学报, 2014,34(4):1045-1053.

[15] Sheng F L; Shih M L; Jyh-Y C; Chin-T L.A Novel Two-Stage Impulse Noise Removal Technique Based on Neural Networks and Fuzzy Decision. Fuzzy Systems, 2008,16(4):863-873.

[16] 王焕松,雷 坤,李子成,邓义祥,等.辽东湾海域水体富营养化的模糊综合评价 [J]. 环境科学研究, 2010,23(4):0413-0419.

[17] 智国铮,陈耀宁,袁兴中,等.基于延拓盲数的洞庭湖湖泊综合营养状态评价模型 [J]. 中国环境科学, 2013,33(11):2095-2101.

[18] Zadeh L A. Fuzzy sets [J]. Information and Control,Volume 8, Issue 3, June 1965, Pages 338-353.

[19] 尚佰晓,王 莉,王 爽,等.铁岭莲花湖水体富营养化评价 [J].湿地科学, 2014,12(1):097-101.

[20] 邓大鹏,刘 刚,李学德,等.湖泊富营养化综合评价的坡度加权评分法 [J]. 环境科学学报, 2006,26(8):1386-1392.

[21] 朱丽楠,官 涤,王永军,等.典型湖库富营养化的模糊综合评价研究 [J]. 长江流域资源与环境, 2012,21(9):1131-1136.

[22] 中华人民共和国环境保护部.地表水环境质量评价办法(试行) [Z]. 2011.

[23] Zhang Y, Shen B W. Application of AHP in risk assessment for project and countermeasures for risk [J]. Journal of Water Resources and Architectural Engineering, 2009,7(3):63-66.

[24] Ludmil Mikhailov, Joshua Knowles. Priority Elicitation in the AHP by a Pareto Envelope-Based Selection Algorithm [Z]. 2010, Volume 634, Part 3, 249-257.

[25] 钟振宇,柴立元,刘益贵,等.基于层次分析法的洞庭湖生态安全评估 [J]. 中国环境科学, 2010,30(S1):41-45.

[26] 史 静,俎晓静,张乃明,等.滇池草海沉积物磷形态、空间分布特征及影响因素 [J]. 中国环境科学, 2013,33(10):1808-1813.

[27] 杜 耘,陈 萍, Kieko SATO.洪湖水环境现状及主导因子分析[J]. 长江流域资源与环境, 2005,14(4):0481-0485.

[28] 宋 戈,雷国平.资源型城市土地集约利用评价研究——理论·方法·应用 [M]. 北京:科学出版社, 2012.

[29] 金相灿,刘鸿亮,屠瑛清,等.中国湖泊富营养化 [M]. 北京:中国环境科学出版社, 1990.

[30] 杨纶标,高英仪.模糊数学原理及应用 [M]. 广州:华南理工大学出版社, 2003:139-146.

[31] 舒金华.中国湖泊富营养化程度评价 [J]. 海洋与湖沼, 1993, 24(6):616-620.

[32] 王贵作,任立良,王 斌,等.基于投影寻踪的湖泊富营养化程度评价模型 [J]. 水资源保护, 2009,25(5):14-18.

[33] Strobl R O, Forte F, Pennetta L. Application of artificial neural networks for classifying lake eutrophication status [J]. Lakes & Reservoirs: Research and Management, 2007,12(1):15-25.

[34] 沈晓飞,马 巍,罗佳翠,等.湖库富营养状态评价及适用性分析[J]. 中国水利水电科学研究院学报, 2013,11(1):74-80.

An improved fuzzy comprehensive evaluation method of eutrophication for lakes and reservoirs.

CHEN Li-li1,2, JIN

La-hua (1.School of Environment, Jinan University, Guangzhou 510632, China；2.Key Laboratory of Water/Soil Toxic Pollutants Control and Bioremediation, Department of Education of Guangdong Province, Guangzhou 510632, China). China Environmental Science, 2014,34(12)：3223～3229

As to characteristics of the nonlinearity of water body eutrophication evaluation system, the randomness of weight assignment and inaccuracy of subordinate function during the process of fuzzy comprehensive evaluation, an improved fuzzy comprehensive evaluation method has been pointed out through improving the traditional fuzzy comprehensive evaluation method, and it has been applied to evaluate degrees of eutrophication of water body in 24representative lakes and reservoirs in China. During the process of improvement, the analytic hierarchy process was combined with principal component analysis by software SPSS16.0and Yaaph to determine index weights, and the determined evaluation criteria were logarithmically transformed to linear, and also each index membership function of logarithmic and lower semi-trapezoid form corresponding to every trophic levels was generated based on distribution characteristics of detected field data, then the membership degree of each lake or reservoir can be obtained and its eutrophication level can be determined by the principle of maximum membership degree. The result of the improved method has been compared with actual eutrophication status of lakes or reservoirs and evaluated results obtained by present evaluation methods, which shows that the calculating process of the improved method is simple, and its result is true and accurate, thus the method is feasible and practical.

eutrophication；improved fuzzy comprehensive evaluation；analytic hierarchy process；principal component analysis

X524

A

1000-6923(2014)12-3223-071,2*

陈藜藜(1989-),女,湖南益阳人,暨南大学硕士研究生,主要研究方向为环境评价与规划.发表论文1篇.

2014-03-20

东莞市高校科研机构科技计划项目(2012108101002)

* 责任作者, 教授, profjin@163.com