基于霍夫变换的工具痕迹特征提取方法研究

李洪武董 波

（1 辽宁警察学院 辽宁 大连 116036；2 大连恒锐科技股份有限公司 辽宁 大连 116023）

基于霍夫变换的工具痕迹特征提取方法研究

李洪武1董 波2

（1 辽宁警察学院 辽宁 大连 116036；2 大连恒锐科技股份有限公司 辽宁 大连 116023）

利用计算机对线条型工具痕迹进行自动比对的关键是提取特征，基于此，研究了一种基于霍夫变换的工具痕迹特征提取方法，该方法包括图像预处理、边缘检测、霍夫变换、直线模型匹配与聚类、主方向与成痕过程模拟几个步骤，通过以上步骤可以从痕迹图像中提取工具痕迹的直线方程与成痕方向，为后续特征比对提供数据基础。

霍夫变换 工具痕迹 特征提取

线条型工具痕迹数字化比对方法的研究是基于提取痕迹的特征点，利用计算机采用线性图像边缘检测算法和图像匹配技术，利用图像的边缘纹理特征对图像进行比较，并根据这些特征的匹配度统计数据，对工具痕迹之间的相似度做出评价。它的开发研制可以提高检验鉴定的准确度，进而提高此类痕迹的利用率，对于串并案件和提升刑事案件的侦破率具有较大的帮助。构建该工具的技术关键有两个：工具痕迹特征的提取与量化描述，工具特征痕迹特征相似性评价模型构建。前者是后者的研究基础。

1 算法内容

1.1 霍夫变换

霍夫变换(Hough Transform)是图像处理中从图像中识别几何形状的基本方法之一，该方法最早是由霍夫于1959年提出的，直到1981年，Ballard提出利用该变换来检测几何形状是可行的。随着该理论的不断扩充，其应用也变得越来越广泛，也衍生出了很多改进算法。但是，最常用的霍夫变换就是从黑白图像中检测直线，应用场景主要是目标识别与定位，比如卫星图像的桥梁识别、自动驾驶中的路线检测等。

对于霍夫变换的基本原理可以从基于霍夫变换的直线识别过程来理解：在平面直角坐标系（x-y）中，一条直线可以用方程y=kx+b表示。对于直线上一个确定的点(x0，y0)有b=y0-kx0，则该直线也可以变成以-x0为斜率、y0为截距直线，原始的（x-y）坐标系，变成了（k-b）坐标系，那么原始直线上所有的点，在（k-b）坐标系中变成了直线簇，从数据域到参数域的变换就是霍夫变换，这样一来，直线簇公共交点在参数域的坐标值，就是所要检测的直线方程参数。有几个交点，就代表待检测图像中有几条直线。

1.2 基于霍夫变换的工具痕迹特征提取方法工作流程

首先，对采集到的工具痕迹图像通过预处理进行灰度化与去噪，然后利用边缘检测得到边缘图像，利用边缘的坐标集进行霍夫变换，再对检测到的直线进行聚类，并剔除干扰直线，最后利用直线线段拟合，得到成痕过程整体曲线描述，并给出成痕主方向（如图1所示）。

1.3 图像预处理

主要有灰度化处理和灰度归一化两个基本环节。灰度归一化处理的目的是将从灰度上尽量消除由于成像系统不统一带来的成痕灰度差异。灰度化参考模型如下式所示。

式中，I（x，y）代表的是原图灰度；g（x，y）代表的是处理后图灰度；k是灰度缩放系数；b是灰度平移系数。

图1 算法流程图

图2为待检测图像，图3是经过灰度归一化的图像，从结果来看，该步骤同样具有部分图像增强的效果。

图2 待检测图像

图3 灰度归一化图像

1.4 边缘检测

由于工具成痕客体不同，而且客体表面的纹理与工具痕迹之间的关系模型并不固定，因此，此步骤建议采用人工标画成痕区域，消除其他纹理线条的影响。然后进行差分，得到边缘差分值，通过自动阈值二值化得到边缘，采用Sobel算子进行一阶差分，达到边缘检测的目的。由于单纯的边缘检测不带有整体去噪特性，因此，后续的差分去噪、形态学操作、边缘细化等步骤是必不可少的。利用能量均值做二值化阈值，进行图像二值化处理，得到最后的边缘图。

1.5 基于霍夫变换的直线提取

该环节主要参考霍夫变换检测直线的方法，该方法可以将边缘坐标点进行霍夫变换，得到直线方程，同时得到了直线的方向描述，图4是图2经过霍夫变换之后的参数域图像，图5是检测出的图像中直线轨迹所处位置。由图可知，由于边缘图中的直线有很多，得到的结果中会有干扰项存在，所以需要其他方法来剔除边界痕迹，并对其余直线划分类别讨论。

图4 参数域结果

图5 霍夫变换直线检测结果图（检测出直线已在图中标出）

1.6 直线聚类与干扰剔除

聚类方法，其基本理念就是通过对样本划分区域特征统计，得到样本分布中心，从而达到分类的目的，对于直线而言，对其斜率进行二维聚类分析，便可以将同方向的直线归并到同一类别，从而得到主要成痕方向以及各自直线之间的夹角。而边界干扰线可以直接通过直线所在区域判定，直接剔除即可。图6中标记了经过该步骤以后，图2检测到的痕迹直线。分类结果如表1所示。通过计算，主要类别间夹角为13.8度。

图6 直线聚类剔除后结果

表1 痕迹直线分类结果

至此，工具痕迹的主要特征：线条数量、不同线条的方向聚类特征点位置、线条的直线方程描述以及相邻线条间的角度差都计算完毕，以上特征作为工具痕迹特征，用于后续的特征比对。

1.7 成痕过程仿真

这个步骤属于数据可视化的范畴，在上一步中，计算机得到了主要类别的信息与特征，但无法从主观上观察到成痕信息，因此，将上一步中分类完毕的同类直线进行统计拟合，得到整体痕迹线，就可以将直线内容从图像上表现出来，易于观察。通过分析直线间的角度变化差异，可以估计成痕时的工具使用方向，以动画的形式表现出成痕过程，仿真过程的部分图像可参考图7。

2 实验结果与分析

为了检验算法的基本性能，采用了12组工具痕迹图像进行测试，12组图像是通过3种工具留下的，通过各组实验图像结果可知，不同工具之间的数据有较大的差异性，同种工具之间，在主痕迹线的方向、线与线之间的夹角、线条数量上都有较好的相似性，可以考虑利用这些参数构建评分模型。限于篇幅内容，本文给出3种工具的部分仿真结果图，具体内容参考图8。对于相应的图像，其特征描述可参考表2（夹角项是该类别与下一个类别间的夹角，最后一类的夹角值为空）。

图7 不同时刻痕迹仿真过程图像

3 结论

本文给出了基于霍夫变换的工具痕迹特征提取方法，痕迹特征包括痕迹数量、痕迹直线描述与痕迹间夹角三个特征值，对于不同工具所形成的痕迹图像，都可以完成定量检测，并且可以通过过程仿真，动态显示成痕过程，为了提高痕迹检验的效率，利用该特征，需要进一步利用量化评分模型来进行特征比对研究。

图8 三种工具痕迹仿真结果图

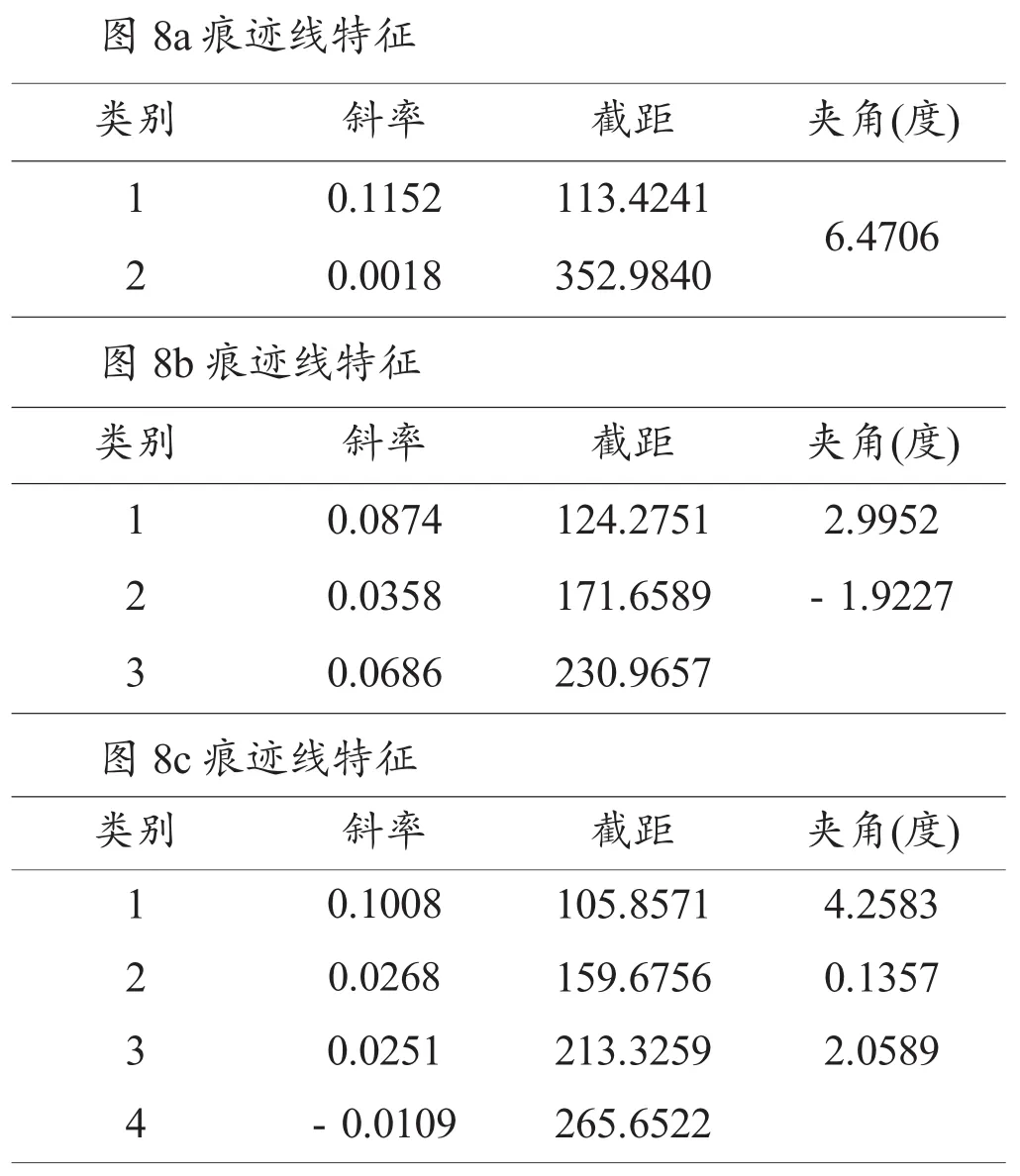
表2 三种不同工具痕迹特征结果

[1]张书杰.工具痕迹学[M].北京：中国人民公安大学出版社，2002.

[2]D.H.Ballard.Generalizingthe Hough Transform to Detect Arbitrary Shapes[J].Pattern Recognition，1981，13(2).

[3]Hartigan,J.A.and Wong，M.A.A K-means clustering algorithm[J].Applied Statistics，1979，28.

（责任编辑：孟凡骞）

D918.3

A

2014-11-07

辽宁省教育厅科学研究一般项目（编号：L2012455）

李洪武（1969-），男，辽宁朝阳人，辽宁警察学院刑事技术系教授，学士，主要从事刑事科学技术教学和科研工作。