基于JC09 光栅尺位移传感器的光栅副间隙分析*

张雪鹏 蔺春波 吴宏圣

(中国科学院长春光学精密机械与物理研究所，吉林 长春130033)

在现代机床和位移控制平台领域中，多采用光栅尺作为刀具和运动部件位置信息反馈的传感器，以提高机床和位移控制台的性能［1-2］。特别是绝对式光栅尺位移传感器，在各种高精度位置控制设备或仪器上应用非常广泛［3］。目前，国内外有很多机构和单位在研发生产光栅尺位移传感器。其中，由长春光机所研发的绝对式JC09 光栅尺直线位移传感器是一款性能优越的产品。在JC09 光栅尺位置传感器中，光栅副即主光栅和指示光栅是该传感器的核心部件之一，光栅副间隙的大小直接影响主光栅和指示光栅所形成的光闸条纹(莫尔条纹)和光电信号的质量。为满足光闸条纹调制度要求，光栅间隙后保证指示光栅处于最佳像面位置［4-5］。同时，还要考虑到灰尘进入光栅间隙中对光栅的磨损以及装配光栅副的误差和成本，所以，光栅副的间隙要处于一个合理的范围内。

本文基于JC09 光栅尺直线位移传感器，分析讨论光栅尺中光栅副间隙的最佳理论位置和允许波动的范围，以及在一般工程实际中综合磨损和经济性之后的范围。

1 光栅副的波列方程

JC09 光栅尺位移传感器的光栅副中，主光栅和指示光栅的条纹间距P1=P2=0.02 mm，属于粗光栅。粗光栅产生的莫尔条纹中虽然一定程度上存在衍射干涉，但不是主要的矛盾，所以完全可以采用几何光学中的遮光阴影原理对莫尔条纹的形成进行解释［6-7］。

当两光栅间的间隙t 值过小时，两光栅在相互运动过程中会因为存在灰尘或者其他污染物、机械误差、振动等因素而使两个光栅面相互刮蹭，损伤光栅刻划面，导致光栅尺可靠性和抗污染能力大大降低，所以两光栅之间的间隙应该保持在一个相对合理的范围。但是两光栅之间如果存在间隙，合成光场将会因此而发生变化。从几何观点看，如图1 所示，与光栅G2叠合的不是光栅G1本身，而是G1投射到G2表面上的影像;从衍射干涉观点看，入射到G2表面上的各光束在两光栅间所走的路程，将随衍射序(对光栅G1而言)的不同而变化，亦即，各序光束到达光栅G2表面时的位相关系不同于它们离开光栅G1表面时的位相关系［8-9］。

光栅副之间的间隙t 对调制光场的影响及其数学表达式，目前还不能够给出准确的结论。但是，可以按信息光学的基本原理来描述和分析此时的调制光场，并建立相应的数表式［8-13］。

假设有一平面波，其具有单位振幅，当它以垂直角度入射到光栅G1表面时，它在G1光栅处的光场可以由式(1)进行描述，即:

根据傅氏光学原理，如果将任意一个光瞳平面上的复合光场分布进行傅里叶分析，那么各个空间频率分量可以看作是沿不同方向传播的平面波［8］;假设X、Y、Z空间坐标轴上第n 级平面波的方向余弦分别用cosαn、cosβn、cosγn来表示，相应n 级次的幅度用Un表示。此时，光线透过光栅G1的平面波列方程可以表示为:

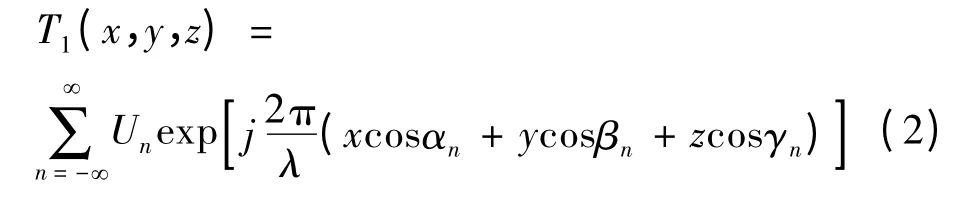
现考虑z =0，这个光栅G1出射的平面，通过对比该平面的傅氏分解式以及波列方程，可以得出:

由此得cos αn=nλ/P1;cos βn=0。显然cos γ 在直角坐标系中不是独立的，它应满足如下条件:cos2α +cos2β+cos2γ=1，

即，cosγn=［1 -(nλ/P1)2］1/2。

因此，光线射出G1光栅后面的平面波波列方程可以表述为:

不难发现，在平面波列传播过程中，只有各谐量的位相发生了变化。这是因为对于某一确定的观测点而言，各分量是沿不同角方向传播到达的，所以各个分量在传播到同一点所经过的路程各不相同，因此需要引入相对位相延迟。也就是说，当光线离开G1光栅出射面到达距离为t 的平面上时，其光场分布可以表述为出射面上光场分布乘以距离位相因子。

同理，从G2光栅出射的第m 级平面波在X、Y 和Z 三个坐标轴上的余弦如果用cosαm、cosβm、cosγm来表示，扰动幅度用Um来表示，那么平面波透过G2光栅后的波列方程可以表述为:

这里，假定G2光栅在Z 方向上离开原点(即G1刻划面)的距离为t。对于G2光栅的入射面，也就是Z=t这个平面，通过对比该平面上的波列方程和傅氏分解式:

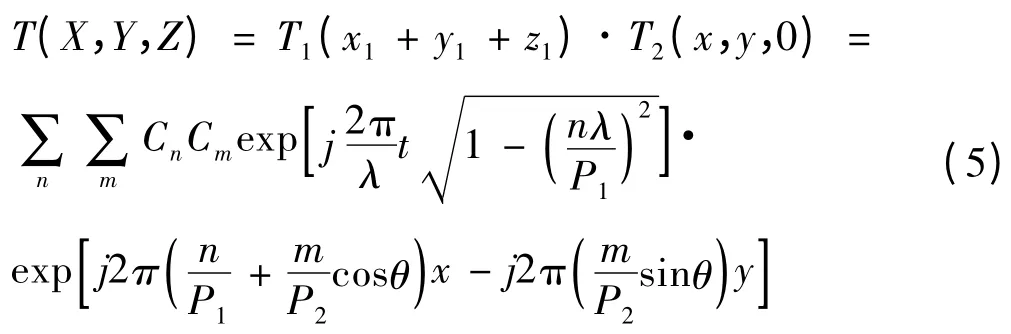
可知:

cosγm= ［1 - (λ/P1P2

将上面关系式代入式(5)，可得光栅副的合成波列式(6)。

应该指出，式(5)中的n 和m 实际上不可能由负无穷大变化到正无穷大，它的范围是有限的，这可由波列方程本身确定，或从光栅方程式解出。这就是光栅副在任意间隙下的光场方程。

2 最佳成像位置的分析和计算

2.1 菲涅尔焦面的分析和计算

正如前面所分析，因为光栅副之间存在间隙，所以平面波列必须引入一个位相因子。即，

由于传播分量应满足(nλ/P1)2＜1 的条件，因此复指数的平方根项可按幂级数展开为:

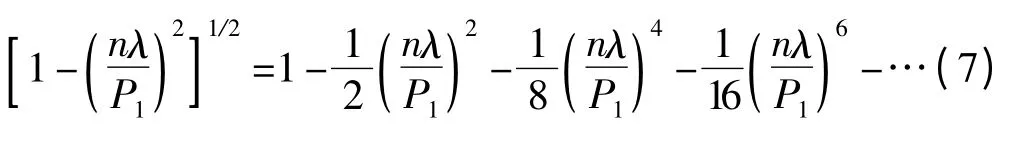
展开式的前两项，则表征间隙影响程度的位相项近似等于:

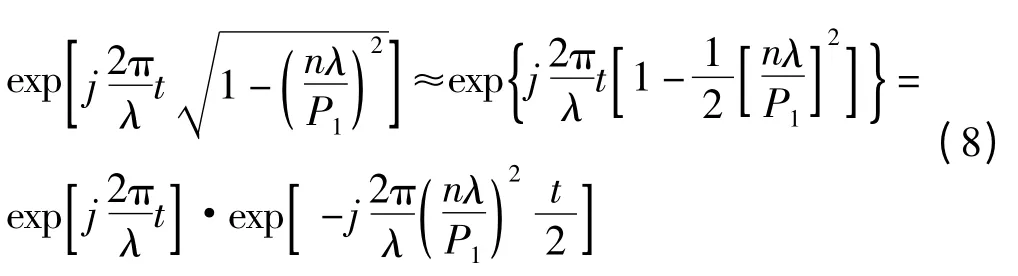
由式(8)可以看出，位相延迟项里面包含两个因子:一个因子只和间隙量t 有关，另一个因子不只和间隙量t 有关，而且还涉及到衍射序n。如果只考虑各分量之间的位相关系变化，那么就可以只考虑后一个因子。可见，当t 满足:

n 序光在光栅G1出射面上的位相关系就会在光栅G2的入射面上再现。同理，对于tn的n 倍位置的平面上，均能得到再现任何序号光束对于零序光的位相关系，也就是得到了光栅G1真的像，它是衍射光的自成像，也就是所谓的泰伯像。

从理论来说，泰伯像显然是周期性出现的、重复的系列像，各序像面与光栅的距离存在如下关系:

式中:N 被称为像面或焦面序数。如果光栅G2位于式(10)所计算出的位置上时，就会如同两个光栅没有任何间隙紧密叠合一样，各个焦面位置上都能够获得清晰的莫尔条纹。

进一步分析可知，即使光栅在(t/2)平面位置上也能自成像，只是所成像的横向位置(X 方向)发生了半个栅距的平移。我们将按:

来定义自成像位置，也就是菲涅尔焦面;序号从1 开始，分别是第一焦面，第二焦面……。证明如下，如图1 所示，间隙量t=P21/λ 的一对光栅副，栅线方向取为Y 轴;O1和O2分别是两光栅与Z 轴的交点;O3是光栅G2上离开O2点为Δx 距离的另一点(x 方向)。平面波列由O1点传播到O2点时，因t=P21/λ，代入式(8)，得到位相项等于exp［jn2π］，这意味偶次波列传到O2时位相不变，而奇次波列经P21/λ 路程后，其相位将改变π。根据相移定理，O3点处的谱分布将是O2点频谱F(nω)乘以相移因子exp［jnωΔx］，当Δx = P1/2时，相移量为exp［jnπ］，可见对于偶次波来讲O3点与O2点同相，而对于奇次波则O3点与O2点反相。综上分析，对于偶次波，因O3与O2同相，O2与O1同相，故O3与O1也同相;对于奇次波，O3与O2反相，O2与O1反相，故O3与O1同相。这就证明，在t=P21/λ 的间隔上也能再现光栅G1的菲涅尔像，只不过像面沿x 方向平移了半个栅距。

2.2 最佳像面位置的分析和计算

前面推导菲涅尔焦面理论位置数学表达式的过程中，相位因子的高次幂被省略了，因累积而造成的相位误差(或称为估算误差)为:

计量光栅常用栅距通常为P =(16～32)λ，相当于每毫米内刻画了50～100 对光栅刻线，那么此时的相位误差则可以表示为:ΔΦn=(0.176°～0.044°)n4。

表1 列出了各序分量所引起的相位误差值，由表1 可知，光线从G1光栅到菲涅尔焦面位置时，各分量的相位改变量跟各分量序数的四次幂成正比关系。若以P1=32λ 的光栅为例，低序波(n =1～4)基本上与G1栅出射面上相同，而到7、8 序时，几乎与G1光栅出射面上反相。亦即，若不计光栅高序分量的幅值影响，理论上在菲涅尔焦面上就不能够获得光栅G1的清晰像。此时，则应该将两光栅之间的间隙量在名义值t附近t±Δt 内作相应微调，目的是使得n 序波的调整相位差δφn，足以补偿累积相位差Δφn对成像清晰度的影响，而对于低序波(特别是基波)，对光栅副之间的间隙微小变化而导致相位误差是不敏感的，如果能够很好地控制Δt，则不会超出理论上清晰成像许可的范围。即最佳成像面的位置应该在光栅副间隙的名义值附近寻找。

表1 各序分量引起的相位误差值

两光栅间隙增加Δt 距离时，根据式(12)，调整位相为:

而在与光栅G1相隔 ( t+Δt )的距离处，因为在泰勒展开式中省略了高次幂所导致的累积相位误差:

根据要求，最佳像面位置应满足δφn+△φn=0 的条件，由此求出间隙调整量为:

由式(15)可知，最佳像面位置对于名义值位置(即菲涅尔焦面)的偏离程度将取决于光栅的谐波分布情况。当高次谐波的幅度较大时，Δt 的值较为可观，有时可达名义间隙的10%。在JC09 光栅尺中，高次谐波已被很好地控制，所以最佳像面位置按照名义值位置选择即可。一般的工程实际中，只要高次谐波不明显，也是允许这样确定最佳位置的。

2.3 光栅副最佳位置的允差分析和计算

当光栅G2偏离光栅G1(或光栅G1的菲涅尔焦面位置)时，各序光束对于参考光之间将产生δφn的调整相位差，从而使干涉图样的对比度降低，并影响系统的测量精度，因此规定名义间隙的允许误差范围是非常必要的。

假定参考光幅值为a0，n 序光幅值为an，干涉图案的对比度为Kn，则由对比度定义可知:案对比度。于是δφn=cos-1(Kn/K0)，由于调整位相

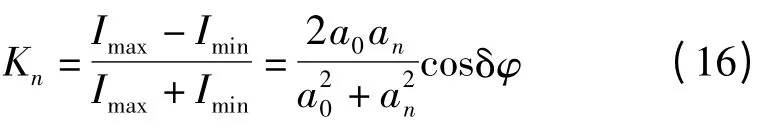
令K0=，表示δφn=0 时的图差δφn与间隙凋量△t 之间存在δφn= ( n2λ△t π )/P2的关系(即式(8))，所以间隙允差δt 可按对比度的许可变化范围求出:

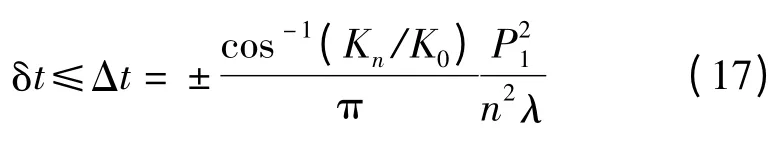
通常，要求Kn不小于0.9K0，那么δφn＜0.14 π。所以δt 可近似取:

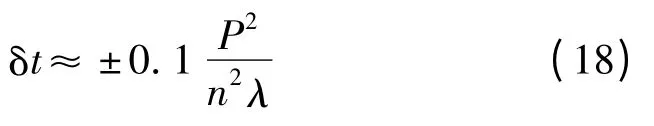
2.4 JC09 光栅尺位移传感器光栅副的间隙计算

把JC09 光栅尺位移传感器光栅副的参数P1=P2=0.02 mm，λ=700 nm 带入式(11)和式(18)，得到其各级菲涅尔焦面:t0=0.057 mm;t1=0.57 mm;t2=1.14 mm…。理论上各级菲涅尔焦面为成像位置，而且随着各级菲涅尔焦面成像质量依次降低。理论最佳成像位置为:t0=0.057 mm，间隙允许的误差为:∂t =±0.057 mm。

而实际上通过试验观察到，当间隙值t0＜t ＜t1/2范围内时，即0.057 mm ＜t ＜0.275 mm，莫尔条纹成像都比较清晰，清晰度与间隙值大小成反比。间隙值超过t1/2 以后，成像开始明显变得模糊。所以对JC09光栅尺位移传感器而言，实际工程中采用的间隙范围还是比较宽松的，可以结合机械磨损、装配工艺和光源强度等因素来灵活确定。一般是在能够满足电子学对信号处理的要求下，尽可能取比较大的间隙。

JC09 光栅尺位移传感器因密封性好，并配有洁净的压缩空气，考虑到磨损、振动等因素，取间隙值0.08 mm，在最佳成像范围内，允许的误差为±0.01 mm。

3 结语

本文按照几何光学的基本原理，分析和计算了基于JC09 光栅尺位移传感器的粗光栅理论上的最佳成像位置和允许波动范围，计算了JC09 光栅尺位移传感器最佳理论位置信息:t0=0.057 mm 以及允许的误差∂t= ±0.057 mm。考虑到光栅副的机械磨损、振动和装配成本、难易程度，结合试验和综合考虑后，给出了JC09 光栅尺位移传感器的光栅副间隙值的实际工程应用范围可以确定在0.08 ±0.01 mm 范围内。

［1］孙强.高精度绝对式光栅尺研究进展及技术难点［J］.世界制造技术与装备市场，2012(5):72 -73.

［2］张宝珠，张峰，刘仙航，等. 一种新型的动态位移传感器- 球栅尺［J］.测控技术，2000，19(1):22 -23.

［3］卢国纲.绝对式光栅尺和编码器是当代位移传感器发展主流——CIMT2011 精密位移传感器评述［J］. 世界制造技术与装备市场，2011(4):56 -60.

［4］纪刚，叶军. 光栅传感器的设计要点分析［J］. 仪表技术与传感器，1995(4):11 -13.

［5］李淑清，李建良，门长峰，等.光栅数字检波器的研究［J］.航空精密制造技术，2004，4(4):19 -22.

［6］孙莹，万秋华，佘容红.小型光电编码器细分误差补偿方法［J］.电子测量与仪器学报，2011，25(7):605 -611.

［7］胡鹏浩，岳盛，党学明，等. Talyrond300 型圆度仪中测角圆光栅的更换与调试［J］.计量技术，2009(8):28 -31.

［8］张帆.高精度光电轴角编码器空间适应性研究与设计［M］.哈尔滨:哈尔滨工业大学出版社，2007:20 -22.

［9］叶盛祥.光电位移精密测量技术［M］. 成都:四川科学技术出版社，2003:8 -9.

［10］张善钟，浦昭邦.光付间隙的确定［J］.仪器仪表学报，1983，4(3):244 -251.

［11］胡毅，费业泰，叶斯然.计量光栅空间位姿参数光场输出模型与仿真［J］.光电工程，2011，38(6)72 -75.

［12］马修水，费业泰，陈晓怀，等.光栅纳米测量的研究与进展［J］.仪表技术与传感器，2006，(4):53 -55.

［13］胡章芳，应俊.减小光栅传感器测量信号误差的研究［J］.重庆邮电大学学报:自然科学版，2007，19(6):697 -701.