基于层次分析法的职称晋升问题建模分析

李兆章

(重庆交通大学 土木建筑学院，中国 重庆400074)

1 问题重述

一学校从事某专业教学与研究的三位讲师，参加评审副教授职务，但是只有一个名额，专业技术评审委员会一直认为，教学效果的重要性比科研成果稍强一些，但要比任现职年限又明显高，科研成果的重要性强于任职年限，通过对甲、乙、丙三位讲师的职称审评材料认真审核，评委得出如下主要信息：

1）任现职年限：甲、乙、丙分别为5年、6年、8年；

2）教学效果：乙比甲突出，丙比甲明显高而比乙稍微高；

3）科研成果：乙丙相当，比甲稍低。

试问这三名教师中，谁的职称应该得到晋升。

2 研究思路与方法

这个问题是与决策有关的问题,且定量的说明了各项指标对三位讲师的影响大小,最后定性的决定选择晋升的对象,所以这是定性与定量相关的题目,于是想到层次分析法（AHP）,这种分析方法可以清晰地反映出诸相关因素(目标、准则、对象)的彼此关系,将所要分析的问题层次化，根据问题的性质和要达到的总目标，将问题分解成不同的组成因素，按照因素间的相互关系及隶属关系，将因素按不同层次聚集组合，形成一个多层分析结构模型，最终归结为最低层（方案、措施、指标等）相对于最高层（总目标）相对重要程度的权值或相对优劣次序的问题，使得决策者能够把复杂的问题简单化,然后进行逐一比较、判断,从中选出最优秀的方案。

3 模型的建立及求解

3.1 递阶层次结构的建立

复杂问题的决策由于涉及到的因素比较复杂，通常是比较困难的，应用AHP的第一步就是将问题涉及到的因素条理化、层次化，构造出一个有层次的递阶层次结构。现在将问题分为三个层次：目标层（O）、准则层（C）、方案层（P），目标层（O）为这三位讲师晋升情况,准则层为：影响晋升者的 3 项指标：任现职年限（C1）、教学效果（C2）、科研成果（C3）,方案层（P）为：三位讲师甲（P1）、乙（P2）、丙（P3）的晋升情况。每个层次有若干元素，各个层次元素间的关系用相连的直线表示。构造出来的递阶层次结构如图1所示。

图1 递阶层次结构

3.2 构造两两比较判断矩阵

层次分析法的特点之一就是定性分析和定量计算相结合，定性问题定量化，在解决问题的第二步就是要在已有层次结构的基础上，通过对准则层各个元素重要性的比较构造两两比较矩阵。

需要注意的是，不要把所有因素一起比较，而是两两比较的方法，对此，需采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。心理学规定共有1到9这9个尺度。先考虑准则层C三个因素对目标层O影响的情况，得到O—C判断矩阵，再次考虑方案层三个因素对准则层三个因素影响的情况，得到C1—P、C2—P、C3—P三个判断矩阵。

表1 O—C判断矩阵A

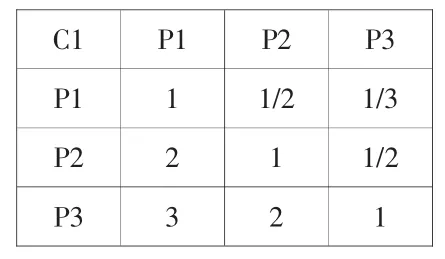
表2 C1—P判断矩阵B1

表3 C2—P判断矩阵B2

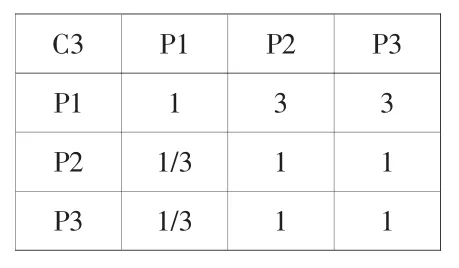
表4 C3—P判断矩阵B3

3.3 层次单排序

层次单排序是指对于上一层而言，本层次的各个因素的重要性的排序，是指每一个判断矩阵各因素针对其准则的相对权重，所以本质上是计算权向量。

首先O—C矩阵A用Matlab计算得到A的权向量为：

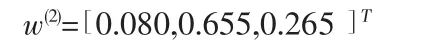
同理，C1—P、C1—P、C1—P 三者分别的判断矩阵 B1、B2、B3 对应的权向量分别为

3.4 层次总排序与一致性检验

一般地，若层次结构由k个层次（目标层算第一层）组成，则方案的优先程度的排序向量为：

各个判断矩阵的一致性检验如表6所示。

表6 判断矩阵一致性检验

可以看出判断矩阵A、B1、B2、B3的一致性是满足要求的。

组合一致性比率CR*=CR(2)+CR(3)=0.0328+0.0561=0.0889＜0.10

故所有判断矩阵的组合一致性是满足要求的。

准则层C和方案层P的总排序如表7、表8所示。

表7 C 层次总排序表

表8 P层次总排序表

从表8可以清晰看出，决策结果是：讲师丙的职称应该得到晋升。

4 问题求解结果分析

根据对排序结果的分析，得出最后的决策方案。

从方案层总排序的结果看，讲师丙的权重（0.5074）远大于甲的权重（0.2253）和乙的权重（0.2683），因此，最终的决策方案是：应该晋升讲师丙的职位。

根据层次排序过程分析决策思路。

对于准则层C的3个因子，任现职年限（C1）的权重最低（0.080），教学效果（C2）的权重最高（0.655），科研成果（C3）的权重（0.265）次之，说明在决策中最看重教学效果，较看重科研成果，而根本不看重任现职年限。

对于最看重的教学效果，丙的单排序权重（0.627）远远高于甲(0.081)，而又是乙(0.292)的两倍多，对于较看重的科研成果，乙和丙的单排序权重(0.200)一样，甲的单排序权重(0.600)大于乙和丙；对于最不看重的任现职年限，丙的单排序权重(0.539)仍然是远高于甲(0.164)和乙(0.297)，由此可以推出，丙由于教学效果较为突出，权重也会相对突出很多。

由此我们可以分析出决策思路，即决策比较看重的是教学效果和科研成果，不太看重任现职年限，因此对于具体因子，教学效果成为主要考虑因素，对于这两个因素，丙在教学效果上比乙和甲突出很多，而在较看重的科研成果方面，丙比乙相当，但比甲差一些，但是教学效果的权重比科研成果大得多，由此，最终的方案选择晋升讲师丙的职称也就顺理成章了。

5 方法评价及改进方法

层次分析法（AHP）将定量分析与定性分析结合起来，按照思维、心理的规律把决策过程层次化、数量化，用决策者的经验判断各衡量目标能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题，其系统灵活简洁的优点，迅速应用地在我国社会经济各个领域内，比如经济计划和管理，能源政策和分配，人才选拔和评价，生产决策，交通运输，科研选题，产业结构，教育，医疗，环境，军事等。

建立递阶层次结构是关键的一步，要有主要决策层参与。构造两两判断矩阵是数量依据，应由经验丰富、判断力强的专家给出。这样得出的数据才更贴近实际，才具有更好的一致性。

层次分析法所用数学工具主要是矩阵运算，用Matlab进行数据处理相当快速、方便。

我们必须同时看到这种方法的不足之处。

首先是它的主观性。从建立层次结构模型到给出成对比较矩阵，人主观因素对整个过程的影响很大，这就使得结果难以让所有的决策者接受。当然采取专家群体判断的办法是克服这个缺点的一种途径。

再者是它的粗略性，该法中的比较、判断以及结果的计算过程都是粗糙的，只用1到9这9个尺度不能非常精确地描述问题，不适用于精度较高的问题，可以尝试寻找其他更好的比较尺度或者寻找其他更好的评价方法。最后是它的囿旧性，即只能从原有的方案中优选一个出来，没有办法得出更好的新方案。

［1］周凯,宋军全,邬学军.数学建模竞赛入门与提高[M].浙江大学出版社,2012

［2］王正林,龚纯,何倩.精通MATLAB科学计算[M].电子工业出版社.2012(3).

［3］张志涌,等.Matlab教程R2012a[M].北京航空航天大学出版社,2010.

［4］田世海.管理运筹学[M].科学出版社,2011.