磁场中双量子位Heisenberg模型的纠缠与量子相变
黄海林,孙照宇
(武汉轻工大学电气与电子工程学院,湖北武汉430023)
Kamta等以两量子位Heisenberg XY链为例,分析了均匀外磁场对热纠缠的影响[1-3],指出任何有限温度下无论怎样调节所加外磁场的强度都存在着有限的纠缠,且临界温度Tc(温度T大于Tc时无纠缠)与外磁场无关。N.Canosa等在Kamta等人的工作基础上进一步探讨了两量子位Heisenberg XYZ链在均匀外磁场作用下的纠缠温度阈值与分离条件[4]。非均匀磁场作用下,Zhang 等[5]分析了两量子位Heisenberg XXZ自旋链的热纠缠,结果表明:随着外磁场的z-分量耦合相互作用的增强,有限温度下的纠缠不断增加,而非均匀磁场的临界值与z-分量耦合相互作用无关,且对称于磁场的非均匀性。同时还发现随着磁场的非均匀性加剧,可获得的最大纠缠变小,磁场的临界值增大。基态纠缠与z-分量耦合相互作用无关。然而实验上磁场方向的调控具有很强的可操作性。本文以Heisenberg XX链为例,从理论上分析磁场方向对纠缠的影响。
1 哈密顿量及其本征解
两量子位各向同性Heisenberg模型在任意一方向外磁场的作用下,其哈密顿量可写为:
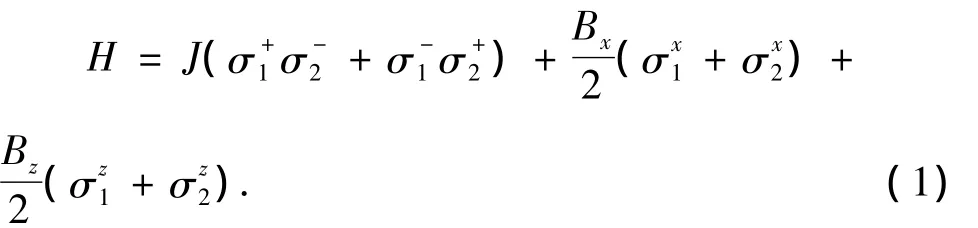
不难算得哈密顿量的本征态为:

此外,ξ(0≤ξ≤1)描述了磁场的方向,不妨称之为方向参数,在下面的分析中不再使用参数α,而用方向参数ξ。当磁场与Z轴平行时ξ=1,当磁场与Z轴垂直时ξ=0。而ξ的值在0到1之间连续变化时,表示磁场的方向在包含Z轴的平面内变化。
2 基态纠缠与量子相变
我们用共形纠缠来度量两量子位的纠缠度,其表达式为:
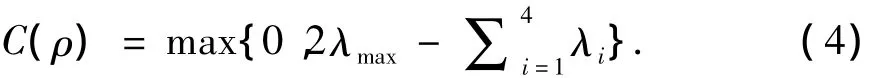
式中 λi为非厄米自旋翻转算符 R =ρ(σy⊗σy)ρ*(σy⊗ σy)的本征值的算术平方根,其中‘*’表示复共轭。
当系统处于无纠缠态时C(ρ)的值为0,处于最大纠缠态时其值为1,C(ρ)的值为0到1之间时,处于系统部分纠缠态。若系统处于某一纯态,即ρ时,(4)式可简单地写为
零温下,由本征解(3)式不难看出,基态能量与磁场有关,即由其大小和方向来决定。若 B >,基态为部分纠缠态 ψ2>,对应的能级为,若B <,基态为完全纠缠态 ψ4>,对应的能级为ε4=-J。
由基态相图(如图1所示)可看出,当磁场取某个确定的值时,总存在一个与之相对应的临界方向参数ξc(0≤ξc≤1),ξ<ξc时,系统的基态为最大纠缠态;同理,当方向参数取某个确定的值时,总存在一个与之相对应的临界磁场B >Bc时,纠缠陡降,也就是说,ξ越过ξc或B越过Bc时,纠缠产生突变,即发生量子相变。
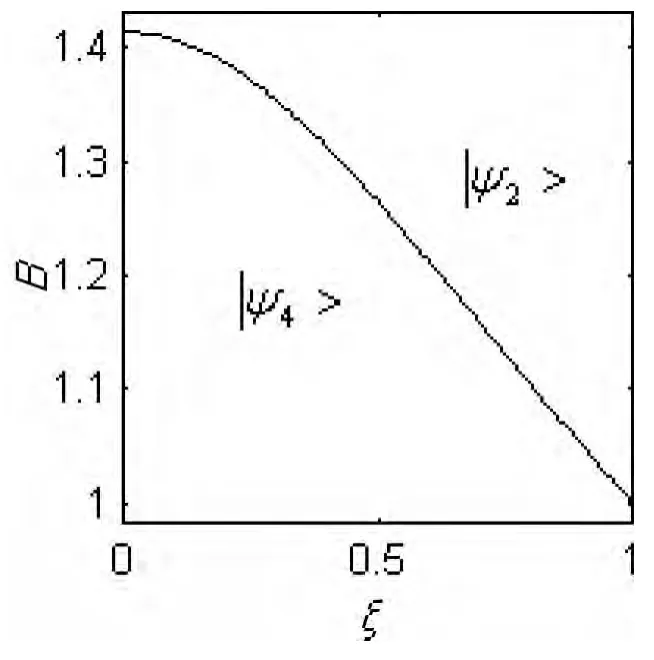
图1 基态相图
为了更清楚地说明参数临界点处的量子相变,我们绘制了零温下共形纠缠随方向参数ξ及磁场大小而变化的关系图,如图2所示。给定ξ,当磁场从零开始不断增强时,纠缠开始保持最大(C=1)不变,当磁场增强到其临界点 Bc(Bc=)时,纠缠突然陡降,发生量子突变。当ξ=1时,Bc的值为最小J,这与文献[6]有着相同的结论。当J<BJ时,方向参数ξ存在临界点处,纠缠同样发生突变,即产生量子突变。通过以上分析可得出:若保持磁场的方向不变,通过改变磁场的大小可获得最大纠缠,反之亦然,在一定范围内调整磁场的方向或大小均可发生量子相变。
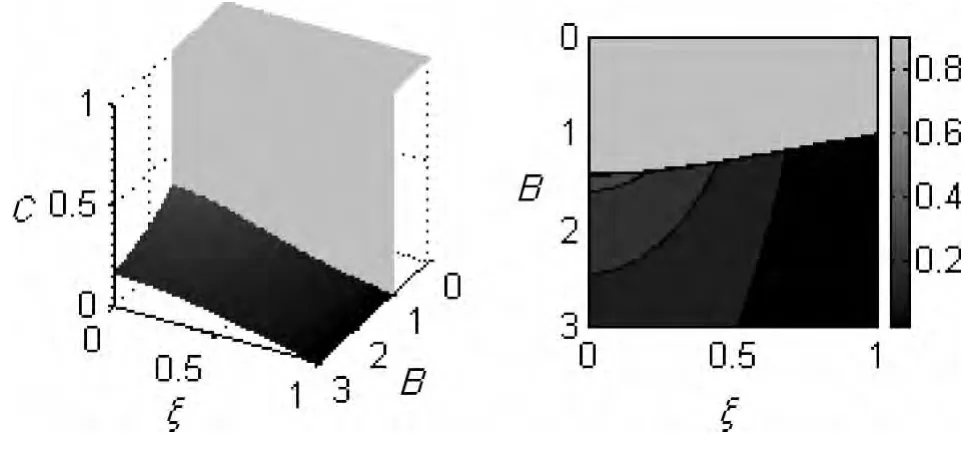
图2 零温下,纠缠随磁场大小及方向的变化
3 热纠缠与临界温度
下面分析有限温度下的纠缠。众所周知,当温度上升时,由于激发态与基态的叠加,纠缠会发生变化,换句话说,随着温度的变化,纠缠的激发态会与无纠缠的基态迭加,或者无纠缠的激发态会与纠缠的基态迭加。非零温下,虽然理论上仍可求出热纠缠的解析表达式,但其形式过于复杂,这里仅给出数值计算结果。
图3给出了在不同的方向参数ξ之下纠缠随磁场B大小和温度T的函数变化关系。仔细观察图中纠缠的变化特性,不难发现图3中每一个图域由3个变化特性不同的区域组成。首先,第一个区域为:B<Bc与T<Tc2,这里的Tc2以及下述的Tc1分别表示第二、第一临界温度。这一区域内,系统处于具有最大纠缠的基态,其能量为 -J,因此,T=0时C=1,随着温度T的上升,最大纠缠的基态与部分纠缠的激发态迭加,结果使得系统的纠缠单调地降低,故可称这一区域为“单调区”。第二个区域为:B>Bc和Tc1<T<Tc2,该区域内,随着温度T的升高,且磁场B趋向临界值Bc,这时纠缠经历一个复苏阶段,正如文献[6]中所述的纠缠复苏现象,故称这一区域为“复苏区”。在此区域内,复苏纠缠随着磁场强度的增加而减小,即纠缠的大小依赖于磁场B的大小。当磁场B增加超过其临界值时,复苏现象不复存在。第三个区域为:B>Bc和T<Tc1,该区域内,T=0时,系统处于非完全纠缠态,即基态为,纠缠随着方向参数ξ的增加而单调地减小。当ξ=1时,纠缠等于零,此时临界温度Tc1也不复存在,这与文献[7]相反,因此,可称这一区域为“方向区”。
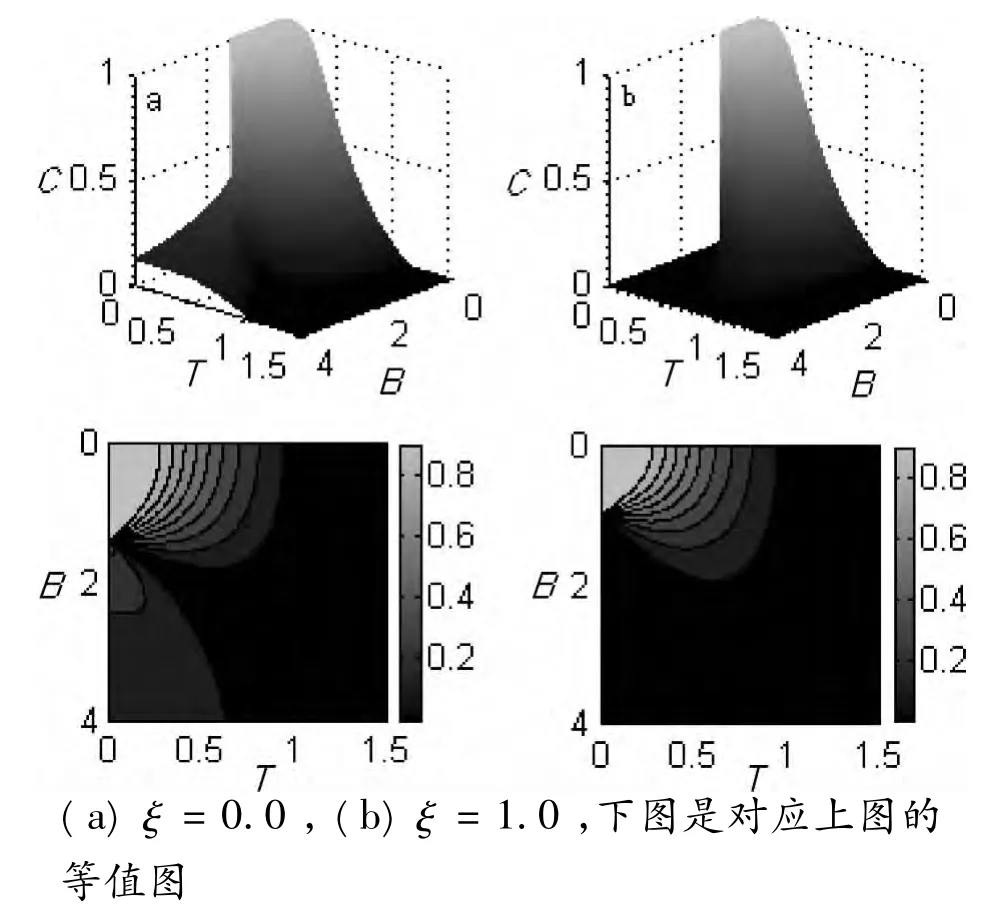
图3 纠缠随温度和磁场的函数变化关系。
为了更清楚地阐述有限温度下方向参数ξ对热纠缠的影响,我们给出了磁场取不同值时纠缠随方向参数ξ和温度T的函数变化关系,如图4所示。为讨论简单起见,不访假设Bc1=J,Bc2=J 。由图4不难发现:(1)B=0.8J(B<Bc1)时,方向参数ξ的临界值ξc不存在,且随着温度的上升,不管ξ取何值,热纠缠始终在“单调区”内变化,一直到温度上升至Tc2为止。(2)B=1.3J(Bc1<B<Bc2)时,方向参数存在着临界值ξc≈0.428 29J,且随着温度的变化,热纠缠要么在“单调区”(ξ<ξc时)内变化,要么在“复苏区”(ξ>ξc时)内变化,一直到温度上升至Tc2为止。(3)B=1.8J(B>Bc2)时,方向参数不存在着临界值ξc,且随着温度的变化,热纠缠要么在“方向区”(T<Tc1时)内变化,要么在“复苏区”(Tc1<T<Tc2时)内变化。(4)B=4.8J(B>Bc2)时,无论ξ取什么值,热纠缠都处于“方向区”(T<Tc1时)内。
同时还发现,临界温度Tc1、Tc2既依赖于磁场B的大小,又与磁场的方向变化有关,Tc1较为敏感,而Tc2则不然。ξ=1时,Tc2=1.14J(这与文献[6]的结论是一致的),Tc1=0。
为进一步阐述上述所得的结论,我们绘出了当磁场的大小和方向参数不同时热纠缠随温度T的函数变化关系。由图5(a)和图5(c)中不难看出,B <Bc2时,Tc2不随B和ξ变化。B>Bc2时,随着ξ的减小或B的增加,Tc2略有所降低。而由图5(b)和图5(d)中不难发现,Tc1随着B的增强而增加,随着ξ的增加而减小。
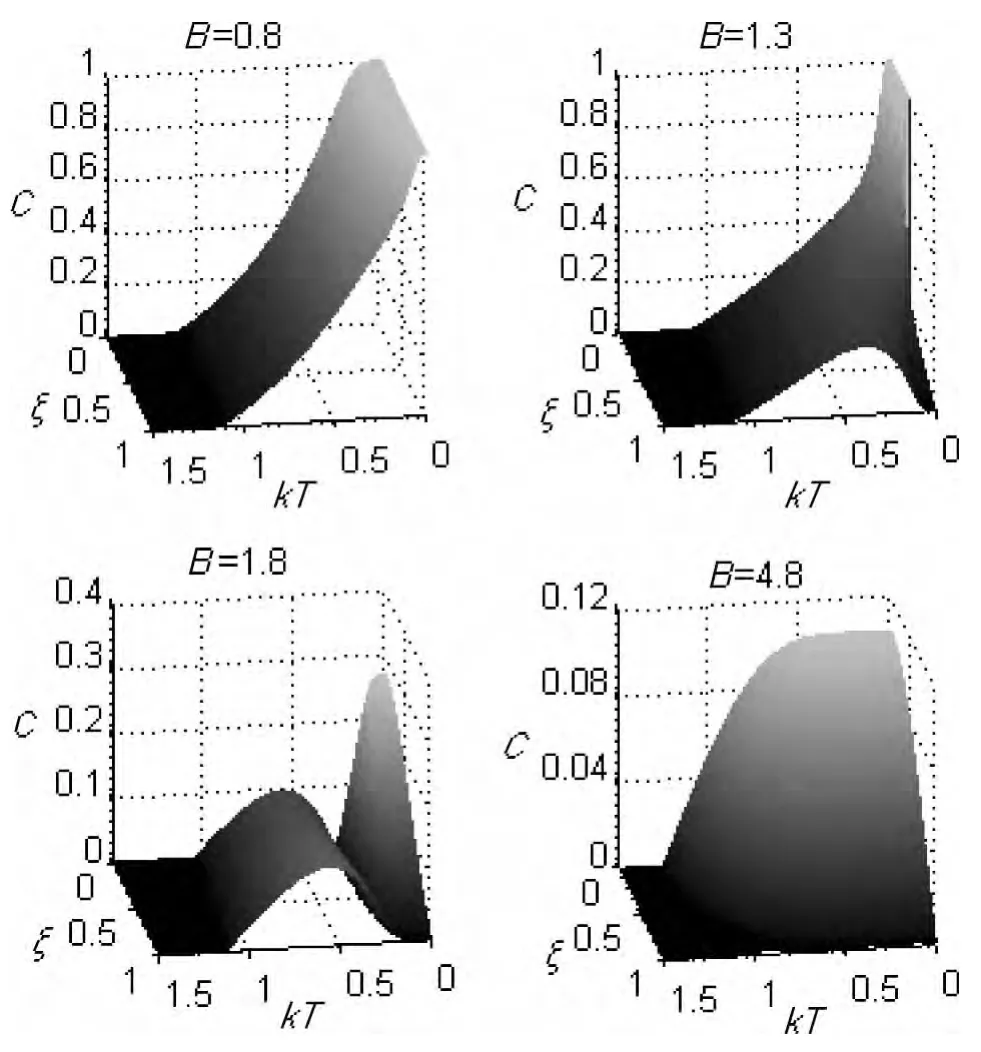
图4 纠缠随方向参数和温度的变化关系。

图5 纠缠随温度的变化关系。
4 结论
本文讨论了外磁场方向和温度对两量子位Heisenberg XX链纠缠的影响,结果发现仅调整外磁场的方向而保持其大小不变可改变系统的纠缠特性。给定温度下,通过改变磁场的方向可获得最大纠缠,即方向诱导纠缠,且阈值温度与磁场的方向有关。令人兴奋的是,改变磁场的方向可发生量子相变,可称之为磁场方向诱导的量子相变。本文的研究结果为实验上提供了一种通过调整磁场方向来调控量子纠缠的有效方法,这在量子通讯和量子信息领域中有一定的意义。
[1]Kamta G L,Starace A F.Anisotropy and Magnetic Field Effects on the Entanglement of a Two Qubit Heisenberg XY Chain[J].Phys Rev Lett,2002,88:107901-107904.
[2]Zhang G F,Liang JQ,Yan QW.Thermal Entanglement in Spin-Dimer V4+with a Strong Magnetic Field[J].Chin Phys Lett,2003,20:452-455.
[3]Sun Y,Chen Y G,Chen H.Thermal entanglement in the two-qubit Heisenberg XY model under a nonuniform external magnetic field[J].Phys Rev A,2003,68:044301(4).
[4]Canosa N,Rossignoli R.Separability conditions and limit temperatures for entanglement detection in two-qubit Heisenberg XYZ models[J].Phys Rev A,2004,69:052306-052312.
[5]Zhang G F,Li SS.Thermal entanglement in a two-qubit Heisenberg XXZ spin chain under an inhomogeneousmagnetic field[J].Phys Rev A,2005,72:034302-034305.
[6]Kheirandish F,Akhtarshenas S J,Mohammadi H.Effect of spin-orbit interaction on entanglement of two-qubit Heisenberg XYZ systems in an inhomogeneousmagnetic field[J].Phys Rev A,2008,77:042309(8).
[7]Wang X.Entanglement in the Quantum Heisenberg XY model[J].Phys Rev A,2001,64:012313.

