基于小波变换和KICA算法的图像盲分离

陈 聪，杨平先，方 洋，何庭杰

(四川理工学院自动化与电子信息学院，四川 自贡 643000)

引 言

图像在采集、使用和保存等过程中容易出现噪声污染、信号叠加等退化现象，而这些影响因素往往都是未知的。盲源分离(Blind Source Separation，BSS)就是在影响因素未知的情况下，根据输入的混合图像信号恢复与重构原始图像［1］。

目前传统的分离方法最要是ICA(Independent Component Analysis，独立分量分析)方法［2-3］，这种方法以非高斯源信号为研究对象，它把各个成分假设是线性独立的，因此在处理非线性信号方面存在一定的缺陷。文献［4］的实验仿真结果表明，在无噪声的情况下，传统的分离方法都有较好的分离效果，但在有噪声的情况下，几种分离效果都不佳。

在图像去噪方面，小波变换能有效地保持图像的细节特征，便于图像盲源分离的后续处理。在处理非线性盲源分离问题方面，新兴的 KICA(Kernel Independent Component Analysis)［5］算法具有较强的非线性处理能力。

由于传统的分离方法没有考虑噪声存在的情况，因此，本文采用小波变换与KICA算法相结合来处理有噪混合图像，并与传统的ICA算法进行仿真比较。仿真结果表明，此方法能较好地分离有噪混合图像。

1 盲源分离问题的描述

盲源分离的描述:假设存在N个源信号S(t)，其中S(t)={s1(t)，s2(t)，…si(t)…sn(t)}T，i∈［1，n］，t为时域中的采样点，并假设各个源信号Si(t)之间相互独立。当N个独立源信号经过某种未知的混合方式与混合矩阵 Am×n相混合，便形成了可观测的信号 X(t)，X(t)={x1(t)，x2(t)，…，xj(t)，…xm(t)}T，j∈［1，m］。由于源信号的数目未知，所以观测信号数目要大于源信号数目(即M ＞N)，盲源分离的数学表示形式:

式(1)中，A为m×n的未知混合矩阵，n为加性噪声。在忽略噪声存在的条件下，盲源分离可表示为:

由于源信号S(t)和混合矩阵A的未知性，想要通过观测信号X(t)分离源信号S(t)，就是要寻求一个分离矩阵W(t)，然后对观测信号X(t)进行分离，获得源信号S(t)的近似估计:

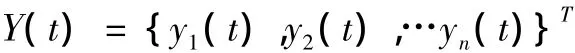
其数学形式:

因此，采用不同的分离矩阵W(t)，可以形成了多种盲源分离算法。

2 小波变换

小波变换是一种新兴的数学工具［6］，它能够处理时域和频域中的局部变换，因此小波变换能有效地从信号中提取有用信息。其基本思想是用一族小波函数系去表示或逼近信号，通过小波母函数的伸缩与平移产生子波，并用其变换系数来描述源信号［7］。

小波函数的表述:

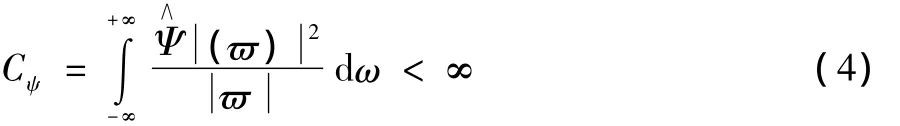
式(4)中函数 ψ(t)为小波母函数。小波基函数系{Ψa，b(t)}是由函数ψ(t)作伸缩和平移变换所得。小波基函数的性质可表示为:

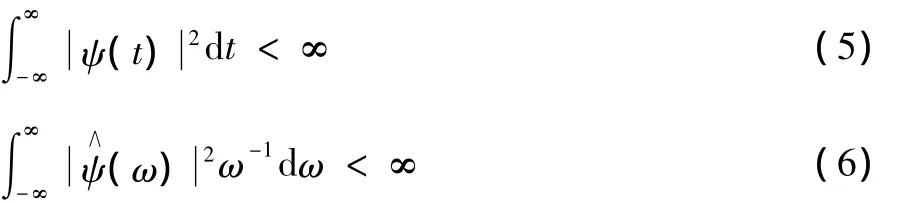
式(5)与式(6)中，

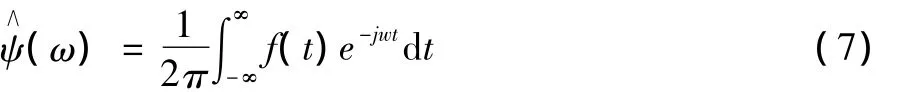
正交函数族:

式(8)中，a为伸缩系数，b为平移系数，a，b∈R2。

则连续的小波变换为:

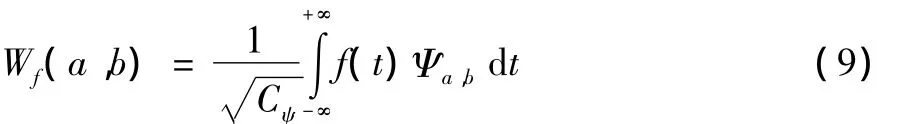
小波逆变换为:

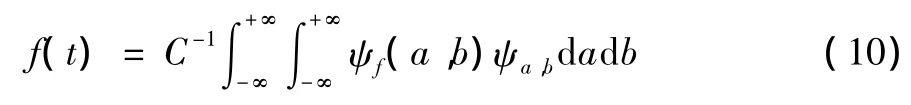
为了方便计算机对信号的处理，要将小波变换离散化。当伸缩和平移因子选取a=2j，b=2jk，可以得到离散的二进小波变换:

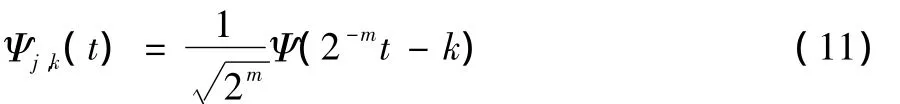
小波变换的实质就是把图像信号分解成不同频带的分量，形成LL(水平低频、垂直低频)、LH(水平低频、垂直高频)、HL(水平高频、垂直低频)、HH(水平高频、垂直高频)的成分。小波变换具有多分辨率和去相关特性，使得小波变换能很好的保留图像的细节特征。

3 小波域中Kernel ICA算法及其实现

使用传统的去噪方法，会在去除噪声的同时损害到图像的细节信息。由于小波变换具有去相关性、多分辨率性和选基灵活性等特点，因此本文选用小波变换对混合图像进行去噪处理。其去噪的基本思路:通过小波变换把含噪图像信号分解到多尺度中，对分解得到的小波系数进行门限阈值量化处理，再对小波作逆变换返回时域，可以实现信号的去噪处理。

小波去噪的关键是如何选择阈值和怎样进行门限阈值处理。小波阈值处理方法可分为硬阈值和软阈值处理。

硬阈值法:

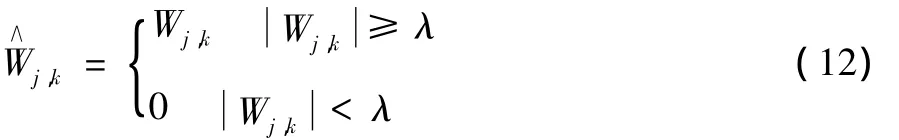
软阈值法:

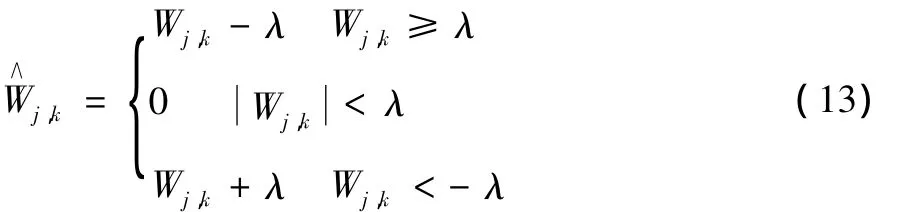
式中，Wj，k为噪声图像的小波变换系数，λ为小波阈值:为图像信号噪声的标准差，即评价噪声的强弱。公式(13)中可以看出，软阈值处理具有一定的平滑作用，故本文采用软阈值的处理方法。

考虑到图像信号间的非线性关系，将KICA分析方法引入到图像处理领域。其基本思想是利用非线性映射，把原输入信号空间Rn中的数据，通过一个非线性函数Φ映射到高维特征空间Rm中:φ:x∈Rn→φ(x)∈Rm。经过非线性映射，使得信号更加容易提取。KICA的假设条件［8］:

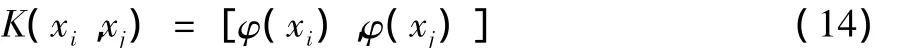
式(14)中K为核函数，在满足该条件的情况下，KICA就是利用核函数代替两向量直接的内积运算来实现非线性变换。常用的核函数有高斯核函数、Sigmoid核函数、Poly核函数。

高斯核函数:

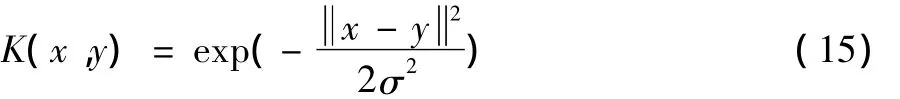
Sigmoid核函数:

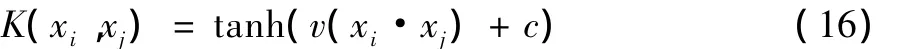
Poly核函数:

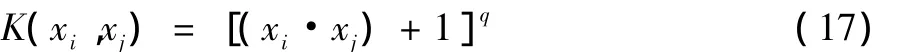
其中，高斯核函数具有局部性强的特点，参数σ越大，外推能力越强。因此本文采用高斯核函数对图像进行分析。

具体的小波域KICA算法步骤如下:

(1)对含噪图像进行小波变换，选择合适的小波和分解层数，获得各层信号和小波分解系数。

(2)对小波系数进行非线性处理。对分解后的小波系数进行阈值量化，获得有效的小波系数。

(3)利用二维小波进行小波逆变换，获得去噪后的重构混合图像。

(4)将混合图像信号变换为一维数组X，得到两个向量的矩阵 X= ［X1，X2］。

(5)给定核函数 Ki，j=K(xi，xj)。

(6)对输入数据作白化处理。

(7)计算中心化Gram矩阵K1，K2，…Km。

(8)计算出分离矩阵Wφ。

(9)由公式(3)求得分解出来的近似信号。

4 计算机仿真实验

选取了3幅像素为256×256的图像作为源信号S1，S2，S3，随机选取了混合矩阵 A3×3:

并对混合图像施加了高斯噪声，仿真效果如图1所示。

为了对分离出的图像进行质量评价，利用信噪比:

其中，PS为信号功率，PN为噪声功率。对混合图像的分离结果作了信噪比的比较结果见表1。由于信噪比越大，说明信号里的噪声越小，由表1的数据可以验证，此分离方法能有效地分离有噪源混合图像。

5 结束语

图1 实验结果

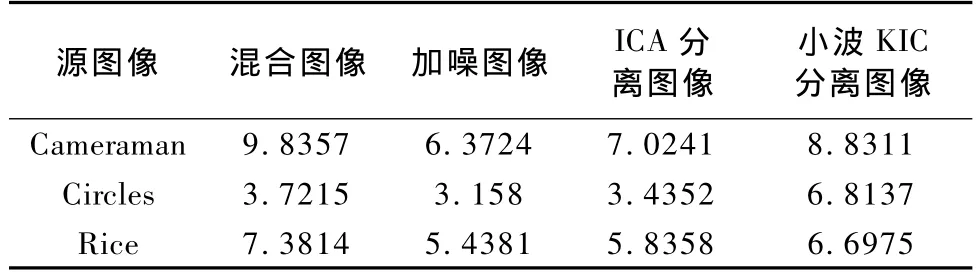
表1 图像信噪比比较

本文对含噪混合图像进行小波消噪处理，有效地消除了混合图像中的噪声，保持了图像的细节特征，并结合KICA算法，解决了含噪混合图像非线性分离的问题。通过本文的方法与传统的ICA处理方法相比较，从仿真结果可知，基于小波变换与KICA相结合的分离效果是显著的，具有切实的应用价值与发展空间。

［1］ Cao X R，Liu R W.General approach to blind source separation［J］.IEEE Trans.Signal Processing，1996，44(3):562-571.

［2］ Hyvarinen A，Oja E.Independent component analysis:a tutorial［J］.Neural Networks，2000，13(45):411-430.

［3］Comom P.Independent component analysis:a new concept［J］.Signal Processing，1994，36(3):287-314.

［4］黄大伟，戴吾蛟，唐成盼.不同ICA算法在图像盲分离应用中的比较分析［J］.工程勘察，2012(4):70-75.

［5］李军，郭琳.基于WKGV-KICA的盲源信号分离算法［J］.控制与决策，2013，28(7):972-977.

［6］周顺勇，李雷.一种改进的小波域图像去噪法［J］.四川理工学院学报:自然科学版，2009，22(3):83-86.

［7］高飞，杨平先，孙兴波.基于小波变换与阈值收缩法的图像增强去噪［J］.四川理工学院学报:自然科学版，2006，19(2):8-11.

［8］田学民，蔡连芳.一种基于KICA-GMM的过程故障检测方法［J］.化工学报，2012，63(9):2859-2863.