基于F直方图的空间方向关系形式化模型

王玉凡，赵占坤，韩晓霞

（河北软件职业技术学院 软件工程系，河北 保定 071001）

基于F直方图的空间方向关系形式化模型

王玉凡，赵占坤，韩晓霞

（河北软件职业技术学院 软件工程系，河北 保定 071001）

空间方向关系形式化模型是判定空间关系的基础，为了提高模型的可靠性，提出了一种基于F直方图的空间方向关系形式化模型。首先给出了基本的F直方图算法，然后提出了基于F直方图的空间方向关系判定方法。采用人工图片作为算例进行实验的结果表明该模型是可行的。

F直方图；空间方向关系；空间关系

0 引言

如何判定和描述空间对象间的空间关系是人工智能领域中一项非常重要的内容，其中建立适用的空间关系形式化模型是判定空间关系的关键[1-2]。作为最重要的空间关系之一，空间方向关系是人们对客观世界进行描述时必须要面对的基本空间关系之一。然而目前在空间关系研究中空间方向关系形式化模型的建立远不如空间拓扑关系和空间距离关系成熟，所以研究可靠的空间方向关系形式化模型是十分必要的。

1 空间方向关系定义及形式化模型

通常空间关系可以划分为三类：空间方向关系、空间拓扑关系和空间距离关系。本文研究的对象是空间方向关系，文献[2]对此给出了明确的定义：空间方向关系是指在空间中某个观察者（V）在一定空间方向关系参考框架（F）下以一定观察角度（θV）观察到的一个对象（目标对象OT）相对于另一个对象（参考对象OR）的位置，反映了空间对象间的序关系，可以用五元组表达式Dir（V，F，θV，OT，OR）表示。其中观察者、观察角度、目标对象、参考对象以及空间方向关系参考框架是空间方向关系的5个基本要素。

空间方向关系形式化模型的建立与这5个基本要素是直接相关的，目前该研究领域已经提出的形式化模型包括：锥形模型、二维字符串模型、最小外接矩形模型、方向关系矩阵模型、基于Voronoi图的模型和基于直方图的模型等。在上述模型中，基于直方图的模型充分考虑到了对象大小、形状、位置以及距离对空间方向关系判定的影响。文献[3]提出的F直方图模型是该类模型中的代表，本文将在F直方图算法基础上提出新的空间方向关系形式化模型。

2 F直方图算法

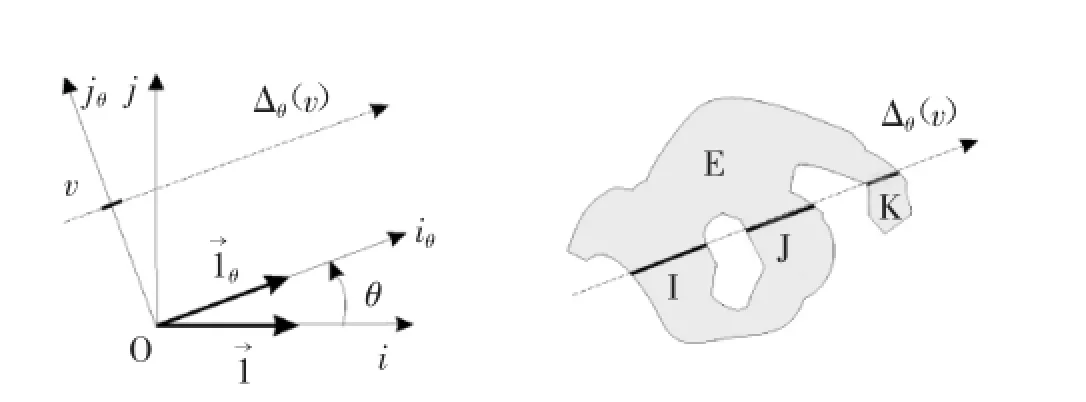
图1 空间方向关系直角坐标系和纵剖线示意图

F直方图算法处理的对象就是空间对象的纵剖线，假设T是关于（θ，Aθ（v），Bθ（v））的集合，θ和v的取值为实数集合R，A和B表示在二维平面上的两个空间对象，Aθ（v）表示空间对象A的纵剖线，Aθ（v）=A∩Δθ（v），同样空间对象B的纵剖线表示为Bθ（v）=B∩Δθ（v）；定义一个纵剖线函数F表示从集合T到集合R+的映射用于描述空间对象A相对空间对象B的空间方向关系，如公式（1）所示。

下面我们要计算空间对象A相对于空间对象B的F直方图FAB（θ），即空间对象A和B在不同角度θ方向上纵剖线之间的函数值F，以θ为变量的函数FAB（θ）则可以看成纵剖线函数值F对截距v进行积分，如公式（2）和图2所示。

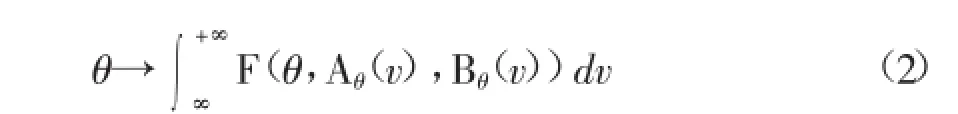
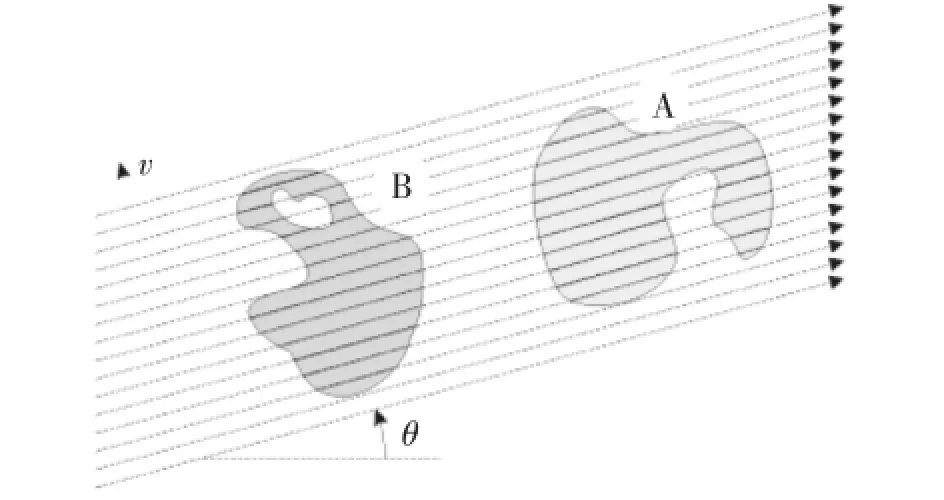
图2 FAB（θ）计算示意图

从物理上FAB（θ）表示对“空间对象A在空间对象B的θ方向上”这一概念的支持程度，我们将在［-π，π］区间内各个方向角度上的支持程度值综合在一起，从而得到F直方图FAB。

3 基于F直方图的空间方向关系判定

首先，需要将FAB（θ）进行归一化处理，获得对应的权值直方图f（θ），则f（θ）可以被看成一个概率分布，该分布以θ为随机变量。

由于人对空间关系描述通常采用定性的方式，如采用“上、下、左、右”进行描述，因此可以采用模糊集的方法实现定量数值与定性描述之间的转换。这里采用四方向空间方向关系，各模糊方向子集“上”、“下”、“左”、“右”的模糊隶属度函数为μ（sin2θ）或μ（cos2θ），如图3所示。

3.1 主要方向和次要方向的判定

根据公式（3）我们可以计算每个基本方向的隶属度值，即公式（3）的四个值相当于四个基本方向在θ概率分布下隶属度值的重心。

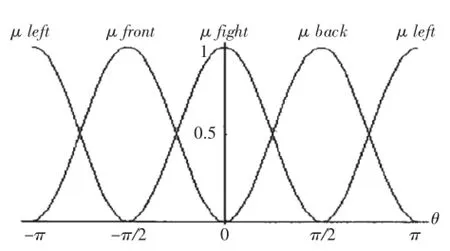
图3 4个基本方向模糊隶属度函数

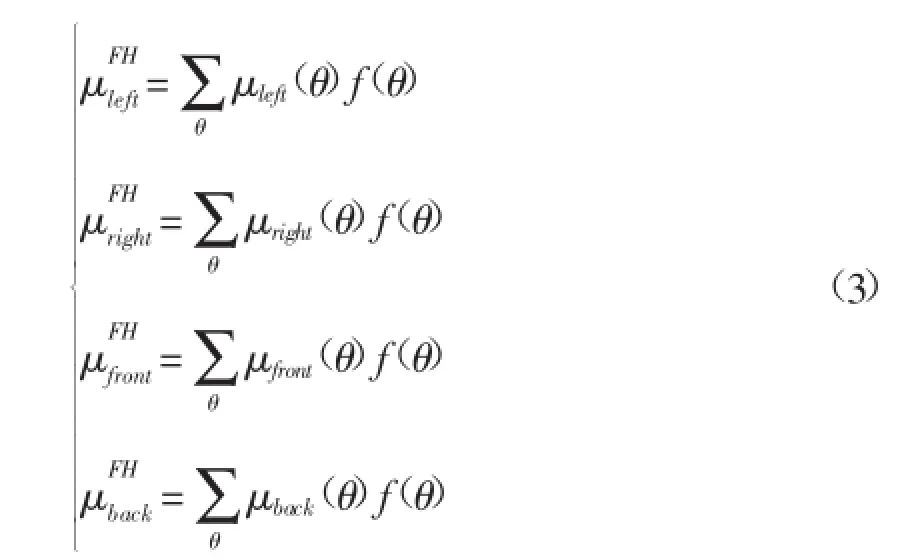
对于每个基本方向，需要考虑它与自己相反方向之间的削弱关系[2]，所以在计算公式（3）后引入公式（4），通过计算公式（4）获得每个基本方向最终的隶属度值，表示了此方向隶属于每个基本方向关系的程度。

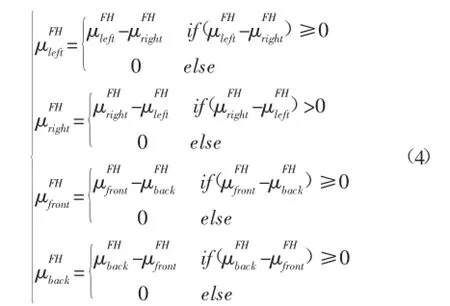
最后，我们将隶属度值最大的基本方向确定为主要方向，将隶属度值第二大的基本方向确定为次要方向。

3.2 “中间”方向关系判定

以上主要方向和次要方向的判定是在各种参考框架下都需要完成的工作，然而在内部参考框架下，除了这些基本方向关系外，还需要判定“中间”这个特殊的空间方向概念。

通过公式（3）（4）我们可以分别计算主要、次要方向的隶属度值，利用该方法得到的主要、次要方向的隶属度值都近似于零时，目标对象通常处于参考对象中间的位置。根据这个特点我们可以结合主要、次要方向的隶属度值μp和μs，通过公式（5）计算“中间”关系的隶属度值，其中“中间”关系的隶属度函数如图4所示。

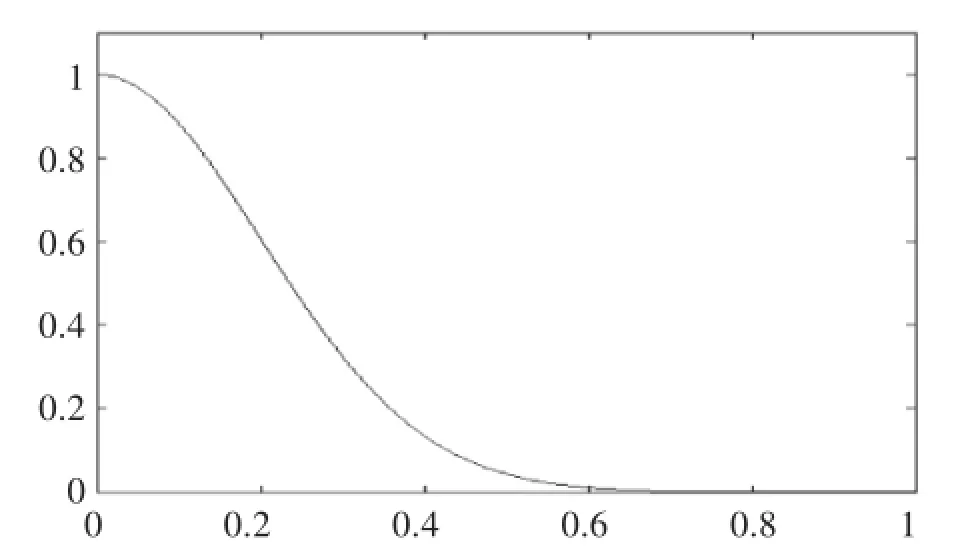
图4 “中间”方向关系的隶属度函数

4 计算实例

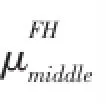
图5 人工图形图例

表1 基于聚合的方向关系词判定结果

5 结论

本文建立了基于F直方图的空间方向关系形式化模型。首先给出了F直方图算法，然后提出了基于F直方图的空间方向关系判定方法，该方法能够判定基本方向关系以及“中间”关系。实验结果表明，基于F直方图的空间方向关系形式化模型能够得到较为接近人对空间方向关系认知的结果。

［1］J.Freeman.The modelling of spatial relations［J］.Computer Graphics and Image Processing，1975，21（7）：27-36.

［2］张珂.二维空间关系描述的研究［D］.北京：北京邮电大学，2012.

［3］Matsakis P.，Wendlling L.ANew Way to Represent the Relative Position between Areal Objects［J］.IEEE Transaction on Pattern Analysis and Machine Intelligence，1999，21（7）：634-644.

Spatial Directional Relations Formal Model based on F-histogram

WANG Yu-fan，ZHAO Zhan-kun，HAN Xiao-xia
（Dept.of Software Engineering，Hebei Software Institute，Hebei Baoding 071001，China）

The spatial directional relations formal model is abase of spatial relations judgment.In ordertoimprovethe reliability of the model，anewspatial directional relations formal model based on F-histogramis proposed.Firstlythe algorithmof F-histogramis presented;secondly anewspatial directional relations judgment method based on F-histogramis proposed in detail.Agood experimental result fromthe synthetic image example showsthatthis model is feasible.

F-histogram;spatial directional relations;spatial relations

TP39

A

1673-2022（2014）02-0048-03

2014－01－10

2013年保定市科学技术研究与发展指导计划项目（13ZG030）

王玉凡（1972-），女，河北保定人，讲师，硕士，研究方向为信息系统与信息安全；赵占坤（1973-），男，河北保定人，讲师，硕士，研究方向为计算机应用；韩晓霞（1974-），女，河北保定人，讲师，硕士，研究方向为计算机应用。