利用声波速度测井估算海域天然气水合物饱和度
林霖,梁劲,郭依群,陆敬安,梁金强
(广州海洋地质调查局,国土资源部海底矿产资源重点实验室,广东 广州 510760)
0 引 言
2007年中国在南海北部神狐海域实施了天然气水合物钻探工作,在海底190~220 m的深度范围取得了含天然气水合物的海底沉积物样品,并获得了大量针对含水合物地层的地质、地球物理和地球化学方面的资料[1]。电阻率和声波测井是评价天然气水合物储层的主要手段,其测井响应特征为高电阻率和高声波速度。利用阿尔奇公式可以由电阻率估算水合物饱和度[2]。利用声波测井数据估算水合物饱和度的方法,一是利用经验公式,二是依靠岩石物理理论[3]。前人利用阿尔奇公式和热弹性理论[4]估算了神狐海域钻井的天然气水合物饱和度。针对海底浅表未固结的沉积层,新近发展的岩石物理模型能够更好地描述天然气水合物在其中的赋存状态,建立天然气水合物饱和度和地层速度的关系[5-6]。本文利用其中2种实用性较强的模型,预测了神狐海域SH2井的天然气水合物饱和度与声波速度的关系,与钻获的实际测井、取心资料进行对比研究理论模型在该区的适用性问题;并根据测井数据估算天然气水合物饱和度。
1 岩石物理模型
针对含水合物地层,基于不同的微观结构假设可以建立3种岩石物理模型:①颗粒胶结模型;②颗粒接触模型;③包体模型[5](见图1)。对比理论模型和实验室、野外钻探采集的数据表明,把水合物当作固体骨架处理的模型更符合观测结果[6],这并不包括第1类假设水合物为胶结状态的模型。
含水合物的颗粒接触模型(TPEM)由Helgerud等[7]提出。考虑了水合物微观赋存结构的2种极端形式,即水合物完全处于孔隙流体中不与固体颗粒接触,或相反作为一种固体骨架基质[见图1(b)]。野外观测数据[5-6]和实验室测试数据[8]表明,前一种情况不符合实际数据。郭依群等[9]在神狐水合物钻探区应用TPEM模型预测水合物饱和度,对比了2种情况的结果,认为水合物完全存在于孔隙流体中的模型在该区不合适。

图1 含天然气水合物地层岩石物理模型的微观结构
当水合物为固体骨架的一部分时,TPEM模型将其视为矿物颗粒中的一种,使用Hill平均计算矿物颗粒的等效弹性模量。利用Hertz-Mindlin接触理论计算矿物颗粒随机堆叠时的弹性模量,此时的孔隙度称为临界孔隙度。再分别使用Hashin-Strikman上下限描述高于和低于临界孔隙度时的情况;最后使用Gassmann方程计算水饱和时的等效弹性模量。
包体模型主要建立在Biot理论基础上,多位研究者给出了不同的描述含水合物地层的三相介质(固体骨架、水合物和孔隙水)模型[6]。Lee[4]在低频、忽略衰减等近似条件下给出一种简化的三相介质Biot方程(STPBE),计算较为简便,该方法在阿拉斯加冻土带和墨西哥湾地区都有较好的应用效果。
TPEM和STPBE这2个模型都只考虑三相介质且各向均一的情况,在处理固体骨架含多种矿物的情况时使用Hill平均。密度由体平均公式计算。2个模型都部分或全部依赖于Biot-Gassmann理论,对于富含黏土的地层,由于大量束缚水的存在使得模型对水饱和情况的估计失去有效性。上述模型的具体公式请参阅文献[4]和文献[7]。
2 模型参数
作为正演理论模型,含水合物的岩石物理模型主要参数是孔隙度、水合物饱和度和矿物成分及相对含量,可由实验测试和测井数据得到。模型中的其他参数则需要根据不同区域的地质情况给定。对于TPEM模型,需要给定临界孔隙度值φ0(一般为35%~40%)和颗粒的平均接触数C(一般为8.5~10)。这2个参数之间存在如下经验关系[10]

通过数值试验分析,这2个参数对模型计算的结果影响较小,当临界孔隙度值φ0取较大值时,计算出的P波速度略有下降。本文中临界孔隙度取38%,平均接触数按式(1)取8.8。
STPBE模型中有2个自由系数α和ε,前者为固结参数,后者表示水合物在孔隙流体中所占比重,取0表示水合物完全以固体骨架形式存在,取1则水合物完全存在于孔隙流体中。Lee等分析了多个实际数据集发现ε可以取固定值0.12,这表明水合物也少量存在于孔隙流体中影响等效介质的弹性模量[4]。对于这2个不能直接由实测数据确定的模型参数,为避免人工选择引入偏差,本文利用模型正演分析确定其取值。
3 模型正演分析
利用神狐海域SH2井的测井、取心分析数据建立模型,将模型预测的纵波速度与SH2井的速度测井数据进行比较以考察模型的应用效果,并确定模型参数。实测孔隙度由取心样品测试分析得到。水合物饱和度值由原位孔隙水氯离子浓度计算得到[2]。个别样点孔隙度和饱和度测试深度略有差异,但不超过0.4 m。沉积物矿物成分及含量由X射线衍射分析得到[11],由于其在含水合物层上下范围纵向变化较小,可以取其平均值用于建立模型。本文使用的纯矿物弹性参数见表1。
需要说明的是,孔隙度和矿物含量测试时样品中的水合物已经分解,这样测量得到的是水合物形成之前沉积物的原始孔隙度,测量得到的水合物饱和度是其在孔隙空间中所占百分比。另一方面,使用的模型中假设水合物为固体骨架中的一种矿物成分,模型中孔隙度φmod、水合物含量与实测孔隙度φ、水合物饱和度Sgh之间需要进行换算,有

式中,fgh为水合物在固体骨架中的相对含量。
相应的,地层原始的矿物相对含量将随水合物饱和度变化而不同,其关系为

式中,f为测试得到的矿物相对含量;fmod为模型中的矿物相对含量。
不含水合物时模型也必须有较好的预测结果,因此在含水合物层段和不含水合物的层段取2组数据进行比较分析(见表2、表3)。为定量标度实测与理论预测值之间的差异,对这2组数据分别计算测井值和模型计算值之间的欧式距离
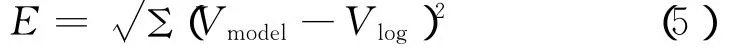
式中,Vmodel为模型计算声波速度;Vlog为声波测井值。该值越小,说明模型计算值越接近实测值。
为确定STPBE模型中的自由参数,以E取最小为标准做参数试验,得到计算值与实测值满足最小二乘的优选系数。对于2组数据,STPBE模型的最优系数并不一致,含水合物层段α=28,ε=0;不含水合物层段α=40,ε在此无意义。计算结果见表2和表3。在含水合物层2个模型都显示出较好的预测能力,与测井数据之差基本在100 m/s以内。最大偏差出现在214.70 m和215.74 m这2个样点处,可能是由孔隙度等值的测量偏差引起。在不含水合物层TPEM模型的E值小于STPBE模型,表明其与测井数据更吻合。从以上结果看,当选取合适的系数后,STPBE模型和TPEM模型在含水合物层段预测效果非常接近,可用于该区水合物饱和度的估算。TPEM模型在不含水合物的层段也显示出较好的预测能力,说明以颗粒接触理论为基础的等效介质模型能比较好地描述海底浅层未固结沉积物的岩石物性,因此也适合用来估算无水合物沉积层的孔隙度。

表1 模型矿物参数
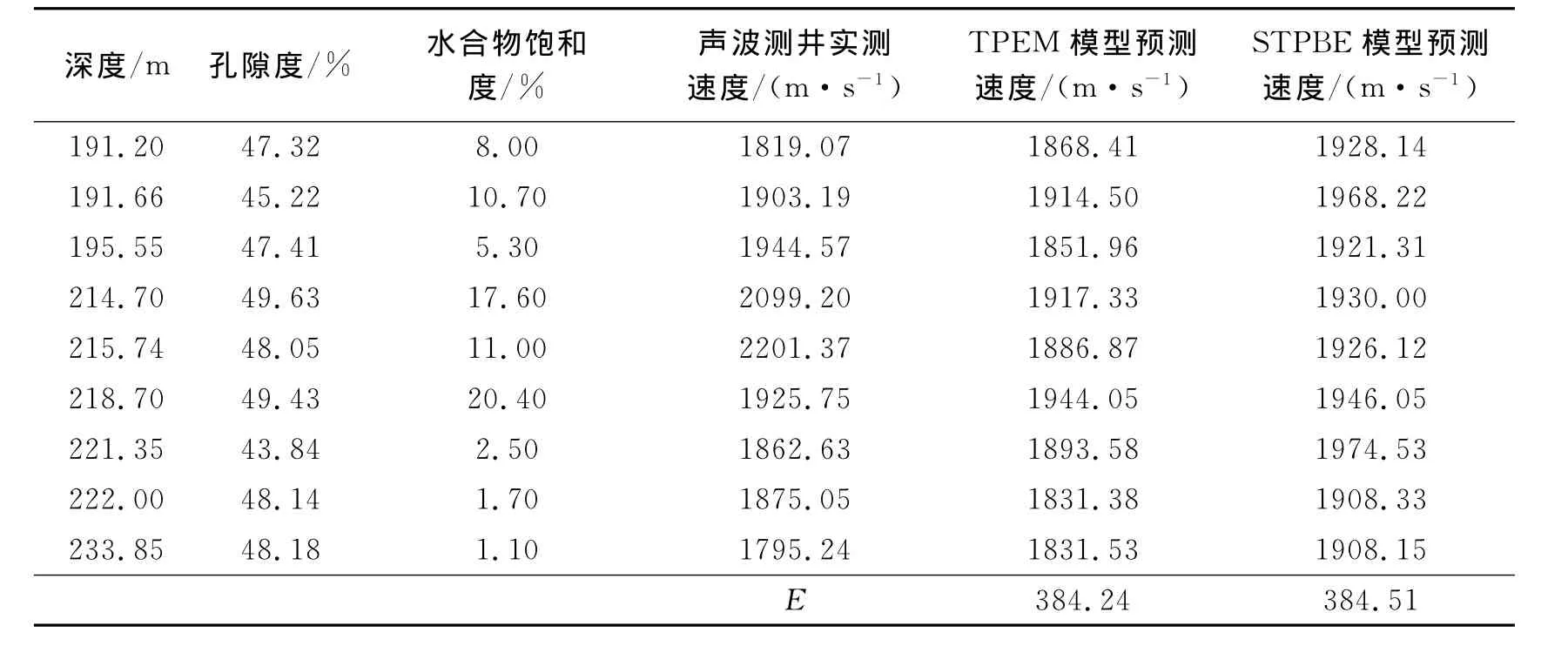
表2 含水合物层段实测数据与模型预测纵波速度

表3 不含水合物层段实测数据与模型预测纵波速度
4 水合物饱和度估算
理想情况下,根据模型方程解出水合物饱和度的计算公式就可以利用实测的纵波和横波速度以及密度数据计算水合物含量。但TPEM模型不能得到解析解,可以采用数值法求解。STPBE模型有解析解,但研究区测井数据中缺乏横波信息,因此仍然采用数值法求取水合物饱和度。
应用这2个模型计算SH2井的水合物饱和度,STPBE模型中的2个自由系数由上述含水合物层正演测试结果确定。孔隙度由密度测井数据计算出,利用测试孔隙度值对结果做校正[12]。TPEM模型和STPBE模型的估算结果总体一致(见图2),前者在一些深度范围估算结果较高于后者。在含水合物层段TPEM模型估算饱和度平均值为35.4%,STPBE模型为29.0%,最大值分别为67.5%和69.4%。模型估算结果与利用孔隙水氯离子浓度估算结果比较,在含水合物层段内显示出一致的趋势,在205~217 m深度段模型估算结果稍微高于后者。
5 讨 论
利用SH2井的测井、取心分析数据确定STPBE模型的ε系数为0,表示天然气水合物在这里的微观赋存是不影响孔隙流体弹性模量的一种形式,即可以将其看作是一种固体矿物成分[4]。这与墨西哥湾等地区的数据显示的情况不同,其可能的原因是该区以细粒沉积为主,而水合物饱和度较低,以细小颗粒的形式存在于沉积物中,不同于上述地区以砂层为主且水合物饱和度较高的情况。
应该注意到用来标定系数的岩心分析数据其水合物饱和度不超过21%,而ε系数在低饱和度情况下对模型的影响很小。图3给出其他参数不变的条件下,模型预测的水合物饱和度和声波速度间的关系,当孔隙度都为40%、ε系数取0或0.12时,STPBE模型在饱和度约60%以上时才有较明显的区别。因此若该区有饱和度较高的含水合物层,ε系数应重新根据实际数据进行标定。

图3 模型预测水合物饱和度与声波速度关系
从图3可以看到在水合物饱和度较小时,TPEM和STPBE模型较为接近,而孔隙度对2个模型的影响都较大,可见孔隙度对水合物饱和度估算精度影响较大。但由于水合物的存在,常规测井方法对含水合物层段孔隙度的计算偏差较大,提高孔隙度计算的准确性有待更进一步的研究。
6 结 论
(1)研究了2种实用性较强的岩石物理模型TPEM和STPBE在神狐海域SH2井的适用性问题,通过实测物性参数和矿物学分析数据确定了适于研究区的模型参数,并利用模型估算了天然气水合物饱和度。
(2)正演分析表明,2个模型对含水合物层的声波速度预测结果非常接近,但在不含水合物的沉积层中TPEM模型效果较好,因此适合用来估算无水合物沉积层的孔隙度。从对水合物饱和度的估算结果看,2个模型对SH2井含水合物层的饱和度估算结果非常接近,TPEM模型估算的饱和度平均值为35.4%,STPBE模型为29.0%,与取心测量氯离子浓度测算的结果保持一致。
(3)TPEM模型估算的饱和度相对较高,但对沉积层背景速度的预测效果较好;STPBE模型计算较为简便,且在有横波数据时可以显式计算水合物饱和度,但对于特定区域,2个自由系数需要通过实际数据标定才能得到较准确的结果。
[1] 陆敬安,杨胜雄,吴能友,等.南海神狐海域天然气水合物地球物理测井评价 [J].现代地质,2008,22(3):447-451.
[2] 王秀娟,吴时国,刘学伟,等.基于电阻率测井的天然气水合物饱和度估算及估算精度分析 [J].现代地质,2010,24(5):993-999.
[3] Lee M W,Waite W F.Estimating Pore-space Gas Hydrate Saturations from Well Log Acoustic Data [J].Geochemistry Geophysics Geosystems,2008,9(7):7-8.
[4] 梁劲,王明君,王宏斌,等.南海神狐海域天然气水合物声波测井速度与饱和度关系分析 [J].现代地质,2009,23(2):217-223.
[5] Dai J,Xu H,Snyder F,et al.Detection and Estimation of Gas Hydrates Using Rock Physics and Seismic Inversion[J].The Leading Edge,2004,23(1):60-66.
[6] Chand S,Minshull T A,Gei D,et al.Elastic Velocity Models for Gas-hydrate-bearing Sediments——A Comparison[J].Geophysical Journal International,2004,159(2):573-590.
[7] Helgerud M B,Dvorkin J,Nur A,et al.Elastic-wave Velocity in Marine Sediments with Gas Hydrates:Effective Medium Modeling [J].Geophysical Research Letters,1999,26(13):2021-2024.
[8] Winters W J,Pecher I A,Waite W F,et al.Physical Properties and Rock Physics Models of Sediment Containing Natural and Laboratory-formed Methane Gas Hydrate[J].American Mineralogist,2004,89:1221-1227.
[9] 郭依群,乔少华,吕万军.基于声波速度分析神狐海域水合物垂向分布特征 [J].海洋地质前沿,2011,27(7):6-12.
[10]Mavko G,Mukerji T,Dvorkin J.The Rock Physics Handbook:Tools for Seismic Analysis of Porous Media[M].New York:Cambridge University Press,2009.
[11]陆红峰,陈弘,陈芳,等.南海神狐海域天然气水合物钻孔沉积物矿物学特征 [J].南海地质研究,2009(20):28-39.
[12]莫修文,陆敬安,沙志彬,等.确定天然气水合物饱和度的测井解释新方法 [J].吉林大学学报:地球科学版,2012,42(4):921-927.

