采用坐标法保证孔系加工精度

陈兴国

(福建瑜鼎机械有限公司，福建 泉州 362000)

根据产品的技术要求，经济合理地确定各有关零件的尺寸公差与形位公差，使产品获得最佳的技术经济效益，这对于保证产品质量与提高产品的设计水平都有重要意义［1］。机械加工制造当中经常遇到壳体、箱体、机身和肘杆之类的零件，这类零件通常都有许多具有相互位置精度的精密圆柱孔组成孔系［2］。孔系分为平行孔系、同轴孔系和交叉孔系。在此仅探讨平行孔系加工中保证孔距精度的方法之一——坐标法。

1 孔系中心距的算法与原理

坐标法是在普通卧式镗床、坐标镗床或数控镗铣床等设备上，借助于测量装置，调整机床主轴与工件间在水平和垂直方向的相对位置来保证孔距精度的一种镗孔方法［3］。

尺寸链中常见的是直线尺寸链，平面尺寸链和空间尺寸链可以用坐标投影法转换为直线尺寸链［4］。采用坐标法镗孔之前，必须把各孔距尺寸及公差借助三角几何关系及工艺尺寸链规律换算成以主轴孔中心为原点的相互垂直的坐标尺寸及公差。

图1a 为二轴孔的坐标尺寸及公差计算的示意图。已知两孔中心距LAB及XAB值。加工时，先镗孔A，调整机床在X 轴方向移动XAB、在Y 轴方向移动YAB，再加工孔B。由此可见，中心距LAB是由XAB和YAB间接保证的。值得注意的是，在计算过程中应把中心距的公差化为对称偏差。

如图1b 所示，由几何关系得:

对上式取全微分得:

对式(2)以增量代替各个微分并整理得:

采用等公差法并以公差值代替增量，即令ΔXAB=ΔYAB=ε，则:

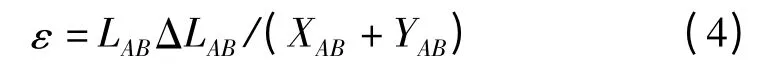
式(4)即尺寸链公差计算的一般公式。

2 实例

如图2 所示，以3 个孔之间保持一定的相互位置要求的情况。其中，XOB=60 mm。加工时，镗完孔O 后，调整机床在X 方向移动XOB，在Y 方向移动YOB，再加工孔B，然后用同样的方法调整机床，再加工孔A。由此可见，孔B 和孔A 的中心距是由两次加工间接保证的。

先计算(XOB，YOB)和(XOA，YOA)及其公差值，由图2 通过几何计算可得:

在确定坐标公差时，为了计算简便，可分解为几个简单的尺寸链来研究，如图3 所示。首先由图3a 求出满足中心距LAB公差而确定的XAB及YAB的公差。LAB转化为对称偏差，mm=(126.23 ±0.05)mm。

由式(4)得:

但XAB和YAB是间接得到保证的，由图3b 和图3c所示，两尺寸链采用等公差法，即可求出孔B 和孔A的坐标尺寸及公差:

为了保证加工孔系时的孔距精度，在选择原始孔和安排镗孔加工顺序时，应把有孔距精度要求的两个孔的加工顺序紧紧地接连在一起，以减少尺寸累计误差对孔距精度的影响［3］。原始孔选择原则，一是原始孔应有较高的加工尺寸精度和较小的表面粗糙度值，以保证加工过程中检验机床主轴对于坐标原点位置的准确性;二是原始孔尽量位于零件的一侧，依次加工各孔，这样工作台朝一个方向移动，以避免因工作台往返移动由间隙而造成的误差。

采用坐标法的加工孔系的机床由两类:一类是具有较高坐标位移精度、定位精度及测量装置的坐标控制机床，如数控镗铣床、坐标镗床、加工中心等，这类机床可以很方便地采用坐标法加工精度较高的孔系;另一类是没有精密坐标位移装置及测量装置的普通机床，如普通镗床、落地镗床、铣床等，这类机床如采用坐标法加工孔系，可利用块规、百分表等测量工具找正坐标尺寸来保证位置精度，这种方法不需要专用的工艺装备，其定位精度一般可达±0.04 mm，但操作难度大，生产效率低，仅适用于单件小批量生产［3］。

3 结语

对于更多孔系的加工也是同样的道理，只要确定好三角形关系，先通过几何关系计算出尺寸值，再利用式(4)即可简便而精确地计算出公差值，从而保证孔系的加工精度。但由于受到加工设备的限制，往往不能简单地依靠加工机床本身的精度来一次性保证零件的孔距公差。在实际加工时，可先半精镗孔，使用专用工装直接测量实际孔距，再根据计算获得X、Y 坐标轴的移动量，移坐标修改加工，确保精镗后获得更精确的孔距尺寸。

［1］邢闽芳.互换性与测量技术［M］.北京:清华大学出版社，2007.

［2］唐浩.采用相对测量法保证孔系加工精度［J］.机械工人:冷加工，2007，12(7):59.

［3］孟繁智.机械加工先进工艺窍门与新技术应用图示例解及常用技术资料速查手册［M］.哈尔滨:黑龙江文化电子音像出版社，2008.

［4］陈于萍，高晓康.互换性与测量技术［M］.1 版.北京:高等教育出版社，2002.