基于ICA-EMD 与SVM 的滚珠丝杠故障诊断*

孟祥敏 谭继文 战 红

(青岛理工大学机械工程学院，山东 青岛 266033)

滚珠丝杠副是数控机床的关键功能部件，广泛应用于数控机床的各直线轴中，其相关故障会导致数控机床出现机械爬行、定位精度下降以及噪声过大等异常现象，从而影响数控机床的加工品质。因此，滚珠丝杠的故障检测与诊断具有实际的应用意义。现在，滚珠丝杠的故障诊断多靠人工经验或应用简单仪表实现［1-2］，此种诊断方法过程复杂且诊断精度低。智能故障诊断研究不断发展，是近年来研究的热点。故障信号的采集以及特征值提取是智能故障诊断的重要基础，针对采集的不同信号之间相互混叠而影响后续的信号处理的问题，本文采用独立分量分析(ICA)算法将多个观测信号，根据统计独立的原则，通过优化算法分解成若干独立信号成分;针对滚珠丝杠故障时产生的非线性、非平稳的振动信号，本文应用经验模态分解(empirical mode decomposition，EMD)将故障信号分解成若干平稳的本征模函数(IMF)。滚珠丝杠的不同故障在不同频带内的信号能量值也不同，从包含故障信息的IMF 分量中提取能量特征值，结合时域、频域特征值作为支持向量机的输入得到最终诊断结果。

1 ICA 的基本原理

ICA 最初的产生动机是用来解决所谓的鸡尾酒会问题［3-4］。鸡尾酒会问题的目的是将特定说话者的声音从酒会嘈杂的混合声音中分离出，是信号处理中盲源分离(BSS)问题的特例。图像处理、语音信号处理、数据挖掘、模式识别等很多领域都已开始密切关注和广泛应用ICA。

1.1 ICA 的基本模型

实际应用中，观测信号中存在的隐含分量，而观测数据中的分量是相互统计独立的，因而可以使用ICA技术分离或提取隐含分量，提取隐含分量的本质特征。如果有信号观测向量:x=(x1，x2，x3，…，xn)T，源信号为:s=(s1，s2，s3，…，sn)T，每个观测分量是源信号分量的线性组合，即:

其中A 为未知混合矩阵:

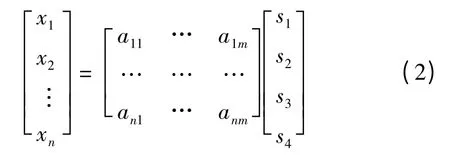
在独立源s 和混合矩阵A 未知的情况下，ICA 寻找分解矩阵W 使得y=Wx 是源信号s 的近似估计值。

1.2 使用条件

源信号s 和加权矩阵A 未知，只有传感器观测到的随机向量x 已知，式(2)有无数解。所以给出以下约束条件:

(1)源信号非高斯分布，至多只有1 个为高斯分布;

(2)源信号各分量间具有数学意义上的相互统计独立性;

(3)假定传感器观测信号与源信号数目相同，即n=m。

1.3 FastICA 算法

FastICA 算法是一种快速寻优迭代算法，又称固定点(fixed-point)算法，分为基于峭度的固定点算法和基于非峭度的固定点算法。本文选用基于非峭度的固定点算法，算法步骤为［5］:

(1)中心化观测数据x 进行零均值处理，再白化处理数据，得到相互正交且能量为1 的白化向量z;

(2)初值化分解矩阵W，且保证‖w‖=1;

(3)进行迭代计算:W(n+1)=E{zG［WT(n)z］}-E{G'［W(n)z］}W(n);

(4)归一化计算:W(n+1)=W(n +1)/‖W(n +1)‖2;

(5)迭代计算直至W 收敛，否则继续步骤(3)迭代运算。

2 EMD 信号处理方法

2.1 EMD 分解流程

EMD 基于自适应分解，是处理非平稳信号的一种有效工具，具有良好的分解性能［6］。根据信号本身具有的特征时间尺度，EMD 将非线性、非平稳信号分解成有限个平稳的固有模态函数(IMF)与1 个余项的和，IMF 能有效反映信号的内部特征。EMD 方法通过下面的步骤对任何复杂信号s(t)进行分解［7］:

(1)求s(t)的所有局部极大值点与极小值点，利用三次样条线在极值点间进行插值计算，形成上下包络线。

(2)计算上下包络线的平均值记为m1，求出h1=s(t)-m1，理想情况下h1为s(t)的第一个IMF。

(3)若h1为s(t)的第一个IMF，则返回步骤(1)(2)直至c1满足IMF 条件。

(4)令r1=s -c1，将r1作为原始数据重复以上步骤，得到第二个满足IMF 的c2，重复n 次，直至rn-1-cn=rn中的rn为单调函数，得到满足IMF 条件的cn。

2.2 EMD 分解条件及分解能力

根据待处理的信号，EMD 有一定的分解条件和分解能力。其分解条件为:(1)待处理的信号有相等的零点数与极点数，至多相差1 个;(2)信号关于时间轴局部对称，即满足在任一点上，由局部极大值确定的包络线以及局部极小值确定的包络线的均值均为零。另外，EMD 分解能力在一定程度上，会受采样频率、边界效应、包络曲线误差等限制。针对能量比相比较大或者组合信号频率比相近的信号，EMD 无法完全分解或正确分解出各单分量。

3 ICA-EMD 工程应用

3.1 基于ICA-EMD 的信号处理

振动信号能很好反映旋转机械的故障状态，针对滚珠丝杠5 种故障状态，本文采用加速度传感器与NI的PXI 4496 采集卡采集滚珠丝杠各种运行状态的振动信号。为了更全面地反映故障状态，在丝杠的X、Y、Z 方向各安放1 个加速度传感器(分别为1、2、3)，以及1 个温度传感器和1 个噪声传感器(分别为4 和5)，传感器安放位置如图1。

加速度传感器1、2、3 分别采集滚珠丝杠3 个方向振动信号，距离很近，采集到的信号会有混叠成分，我们可以从图2 分离后信号的EMD 分解结果图3 看出，由于EMD 的分解能力有限，而当EMD无法正确分解信号时，得到的IMF 为缺陷的IMF，丢失掉了源信号信息。图2 是传感器采集到的丝杠弯曲的原始信号时域波形，图3 是对应的进行处理后的波形。通过ICA 与EMD 结合恢复缺陷IMF 所丢失的信号特性，经过ICA 分离处理后的波形图4 及其EMD 分解结果图5 可以看出，ICA 处理后的信号波形更加规范，其幅值变化更能清楚地显示，能量变化更明显，信号性质可以体现出来。

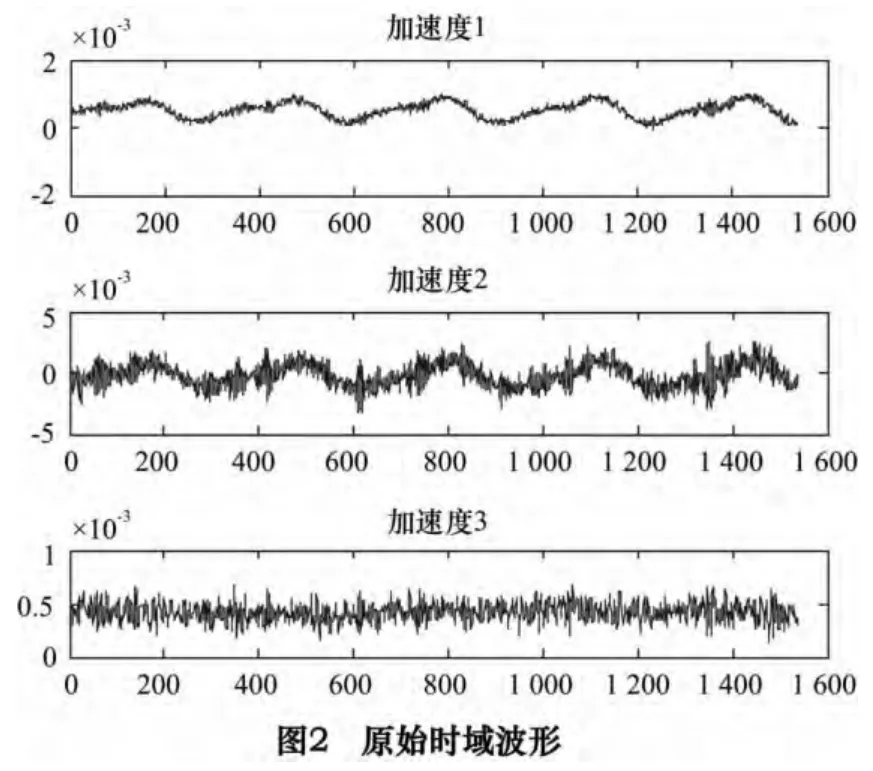
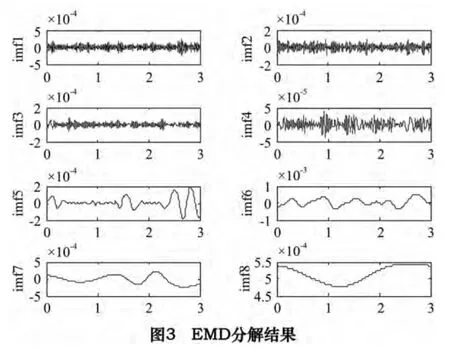
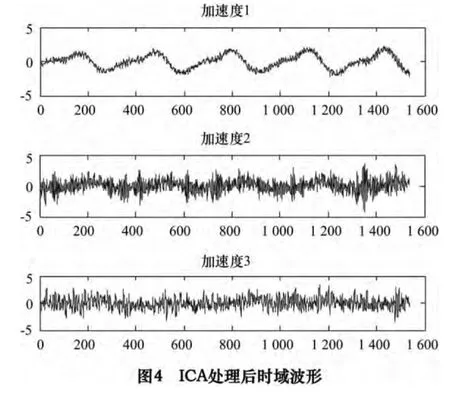
3.2 滚珠丝杆故障诊断

滚珠丝杠不同的类型故障会产生不同频率的振动信号，而振动信号产生相关的共振频率信号、故障信号的能量也随着频率分布而变化。本文用EMD 能量熵可以表现这种变化。

设通过EMD 分解滚珠丝杠振动信号得到n 个IMF 分量和一个余项rn，其能量分别为E1，E2…En，由于IMF 分量c1(t)，c2(t)，…，cn(t)包含不同的频率分量，E={E1，E2…En}形成了滚珠丝杠振动信号在频域上的能量分布，那么相应的EMD 能量熵定义为:

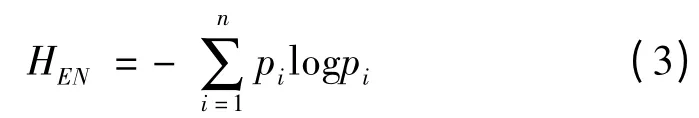
式中，pi=Ei/E 是能量ci(t)在整个信号能量(E=)中所占百分比。

本文针对滚珠丝杠的5 种状态，每种状态选择20组数据，共100 组数据，求取每种状态的平均能量熵，结果如表1 所示。

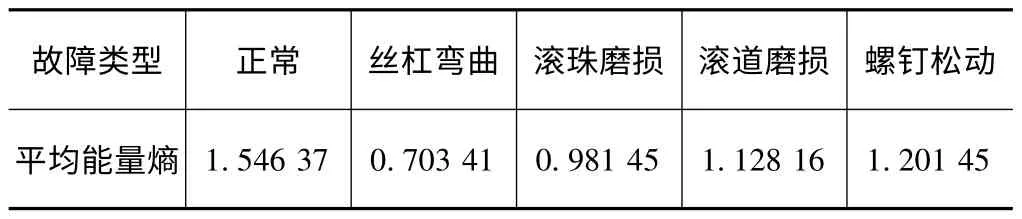
表1 能量熵表

因为正常振动信号中每个频带中的能量分布比较平均且不确定，所以其能量熵最大，其他各种故障状态产生的振动信号，随着频带能量分布的均匀性，其能量熵值都有明显的差别。如丝杠弯曲故障，产生较高的共振频率分量且振动严重，能量大部分集中在共振频带，其能量熵为最小。

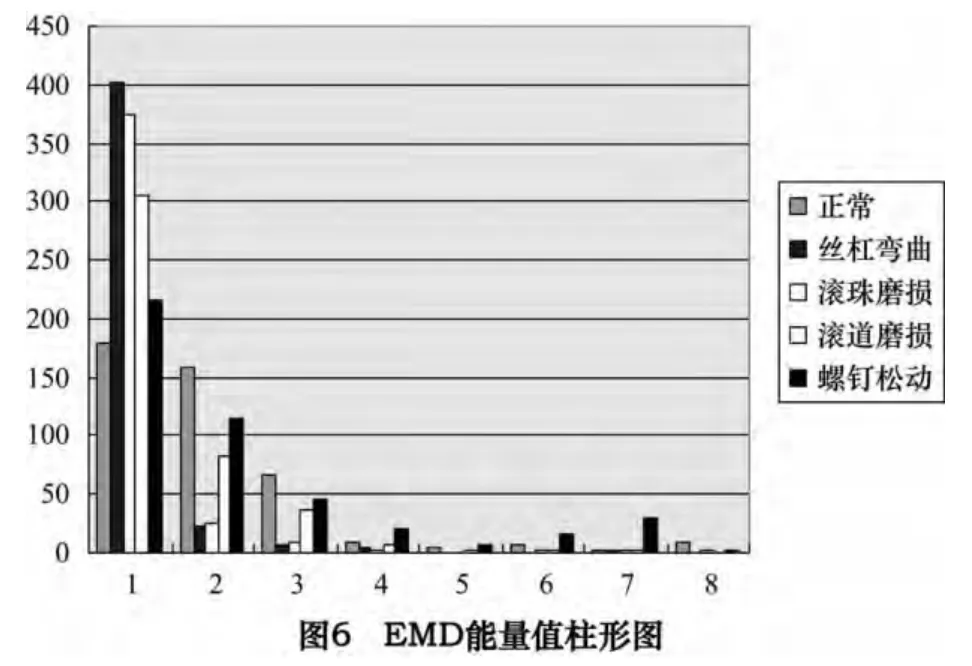
从图6 可以看出EMD 分解后的前3 个IMF 能量可以区别5 种故障状态，选择各种状态振动信号的前3 个IMF 能量值以及振动、噪声、温度信号的时域、频域值，共12 个特征量。针对正常丝杠、丝杠弯曲、滚珠磨损、滚道磨损及螺钉松动5 种状态分别做了50 组试验，类别标签分别为1、2、3、4、5，对滚珠丝杠5 种状态，所以每类故障共得50 组12 维特征向量。在50 组数据中随机选取46 组组成训练集，每种状态剩余的4组组成测试集作为支持向量机(SVM)的输入。测试集数据如表2 所示。

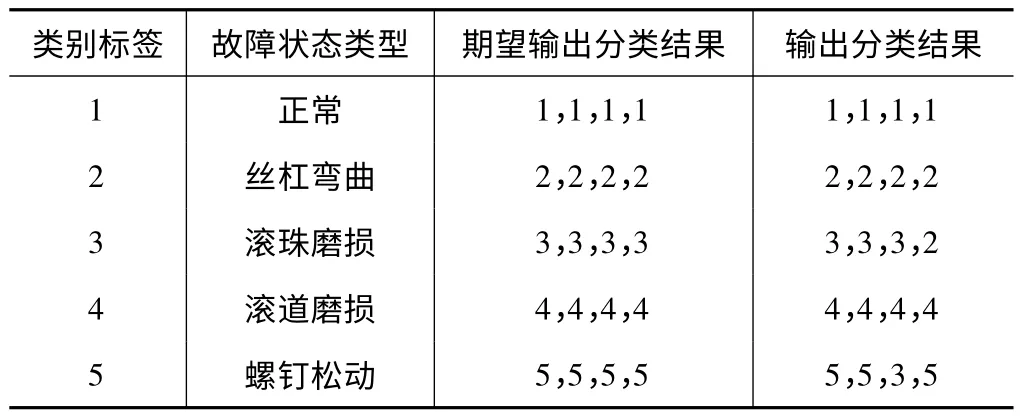
表2 滚珠丝杠故障诊断结果

诊断结果显示只有滚珠磨损及螺钉松动各一组数据诊断失误，诊断结果正确率达到90%。

4 结语

EMD 是处理非平稳信号的十分有效的时频处理方法，但由于信号本身的性质，EMD 有时无法正确分解信号，因此分解出的IMF 为缺陷的，不能完全体现出信号性质。而盲源分离技术，在没有先验知识的情况下，可以依据传感器采集的观测信号，恢复出机械部件的振源信号。本文用ICA 与IMF 相结合的方法，为了解决EMD 分解能力受到限制的问题，恢复缺陷的IMF 表现的信号性质。最终计算各IMF 能量，IMF 能量可以有效辨别不同的故障状态。

［1］唐利平.滚珠丝杠螺母副误差补偿及故障诊断［J］.中国科技信息，2006(23):73 -76.

［2］翟建军，王召颖.三点检测法检测数控机床滚珠丝杠副故障［C］∥第八届全国设备与维修工程学术会议暨第十三届全国设备监测与诊断学术会议.北京:机械工业出版社，2008:704 -706.

［3］Liu M，Wang X，Zhao H.Research on illegal information flow in role—based access control model based on petri net［C］.ICIC Express Letters，2012，6(1):139 -144.

［4］杨竹青，胡德文.独立成分分析方法在盲源信号分离中的应用［J］.计算机测量与控制，2002，10(3):200 -202.

［5］Hyvarinen A.Fast and robust fixed-point algorithms for inde-pendent component analysis［J］.IEEE Transactions on Neural Networks，1999，8(3):622 -634.

［6］Huang N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc R SocLond A，1998;454(1971):903 -995.

［7］蔡艳平，李艾华，石林锁，等.基于EMD 与谱峭度的滚动轴承故障检测改进包络谱分析.振动与冲击，2011;30(2):167 -172.