基于Petri的改进优先级队列缓存管理分析与仿真＊

王 霞，姜宏岸

（淮海工学院 计算机工程学院，江苏 连云港 222005）

随着网络环境中多媒体业务需求的快速增加，用户对于数据传输服务质量的要求越来越高，缓存管理是网络服务质量控制的关键技术之一，也是实现网络拥塞控制的重要手段。缓存管理是对网络传输节点中缓冲存储器队列资源的管理，网络中的传输节点通常采用队列缓存、延迟转发的服务方式来提高输出链路的带宽利用率。

Petri网［1］是很多系统和领域用来描述系统模型的有力的图形和数学模型工具之一，Petri网可以通过建立状态方程和其它数学模型来描述模型的形式，进行正确性验证以及系统性能的评价等。自随机Petri网提出以来，系统性能评价已经成为Petri网最成功的应用领域之一。而排队网络［2］在随机模型应用领域是传统的数学模型工具，在计算机网络、传统控制系统等方面有着广泛的应用。

本文提出的方法是基于Petri网模型并利用排队理论对缓存管理机制的性能进行建模研究，并通过相应仿真工具仿真，最后分析仿真结果。

1 缓存管理分析

1.1 传统的缓存管理机制

网络节点中的缓存管理通常采用先入先出（FIFO）方式，当缓存队列满时就不再接受新的报文。进行缓存管理机制的性能分析时，要用到排队理论中的里托定理（Little’s Law）［3］。该定理给出了趋于稳定状态时，排队系统中顾客数量N、吞吐量λ和每个顾客的平均时延T之间的关系为

将里托定理中的顾客数量作为缓存队列中的数据包数量，就可以通过公式（1）计算出数据包的平均时延。分析时假设采取定长数据包形式，规定数据包的大小与缓存队列中每个单元的大小一致。用参数R表示缓存中数据包的转发率，即每秒转发数据包的数量。设缓存队列的容量为B，用变量n表示缓存队列中数据包的数量，用参数π（n）表示缓存中数据包数量为n时的概率。

当缓存队列占满时将会出现阻塞情况，因此，数据包阻塞的概率为

数据包的吞吐量为

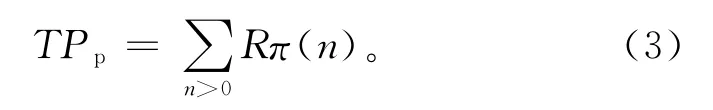
1.2 优先级队列的缓存管理机制

基于优先级队列［4］（PQ）的缓存管理机制在FIFO的基础上进行了改进。其基本实现方法是：系统有两个缓存队列Q1和Q2，其中的Q1用来存放高优先级的实时多媒体数据报；而Q2是用来存放低优先级的普通数据报的。在进行转发时，高优先级队列Q1中的数据报先于低优先级队列Q2中的数据报转发。

1.3 改进的优先级队列的缓存管理机制

本文提出一种改进的优先级队列（IPQ）的缓存管理机制，其思路是：系统有两个缓存队列Q1和Q2，其容量分别为Bh和Bl，其中的Q1用来放高优先级的数据报，Q2用于放高优先级和低优先级的普通数据报。当高优先级数据到来时，若Q1未满则进入Q1，若Q1已满而Q2未满则进入Q2；当低优先级数据到来时，若Q2未满则进入Q2，若Q2已满则该包丢弃。在进行转发时，首先高优先级队列Q1中的数据报优先转发，其次为了避免低优先级的丢弃过多则，如果Q2队列满则先将Q2转发一定数量的数据包，然后再检查Q1中是否有数据包。

对优先级队列的缓存管理机制，根据其工作原理，可得出高优先级数据报的吞吐量为

低优先级数据报的吞吐量为

式中，h为高优先缓存队列中数据包的数量，l为低优先缓存队列中数据包的数量。

2 缓存管理建模

Petri网是排队系统建模和仿真的有力工具。这里采用Petri工具对网络节点的缓存管理进行建模分析。Petri网中引入时间参数的方法是：使用一个随机的延迟联系每个变迁的可实施与实施，这种类型的Petri网叫作随机Petri网（stochastic petri net，SPN）［5］。现实生活中，为了接受某种服务，排队等待是常见的现象。从排队现象得到抽象的物理模型，进一步建立数学模型的一整套理论就是所谓的排队论。

排队模型中最常见的是 M／M／1队列［6］，第1个M表示到达过程是马尔可夫过程（Markovian process，MP），也可精确地说是泊松（Poisson）过程，到达速率为λ；第2个M表示服务时间的分布是马尔可夫过程（负指数），平均服务时间为μ－1。队列中的顾客被服务的原则是先来先服务，M／M／1队列模型，如图1所示。

图1 M／M／1队列模型图Fig.1 M／M／1queuing model diagram

文中提出的改进的优先级队列缓存机制的原理可如图2所示，结合排队理论，优先级原理则可对上述优先级队列的缓存管理机制建立Petri网模型，如图3所示。其中高队列、低队列和数据处理部分还需要设置队列容量的大小和数据处理的随机时间等，具体的实现在仿真图中进行描述。

图2 优先级队列的缓存管理机制Fig.2 Priority queue buffer management mechanism

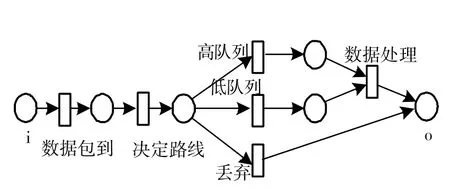
图3 优先级队列缓存管理机制的Petri网模型图Fig.3 Petri net model diagram of priority queue buffer management mechanism

3 缓存管理仿真

研究排队系统的方法有优化和仿真两种。优化主要是利用运筹学中的排队论，而仿真则主要是利用现有的基于离散事件的仿真软件，如Arena，Exspect等。本文采用Exspect软件［7］对排队系统建模的方法，并且对缓存管理中的不同方案进行了分析研究。

3.1 仿真实验

本文所提出的基于Petri网的优先级队列缓存管理机制在Exspect中仿真如图4所示。图4中结点decide需通过Exspect语言［8］实现选择入高队列，入低队列、还是丢弃包操作，结点start－process用于控制数据包的操作处理，给出数据处理的随机时间，并将完成一次服务后的队列数减1。本文仿真过程中假设开始节点以随机的速率产生报文，每个报文处理时间为1～4ms间的随机时间。在decide和start＿process两个结点中使用Exspect语言分别设计两种不同的优先级队列的算法，然后分析仿真结果中每个子过程中到达的数据包的数量、每个子过程数据包的平均时延、监测高低优先级数据包的丢包情况，并根据发送的数据包的数量和数据包的平均时延，通过上面的公式（1）可以计算出系统的吞吐量，当队列满时则可以根据公式（2）和公式（3）计算系统的吞吐量及阻塞概率等。

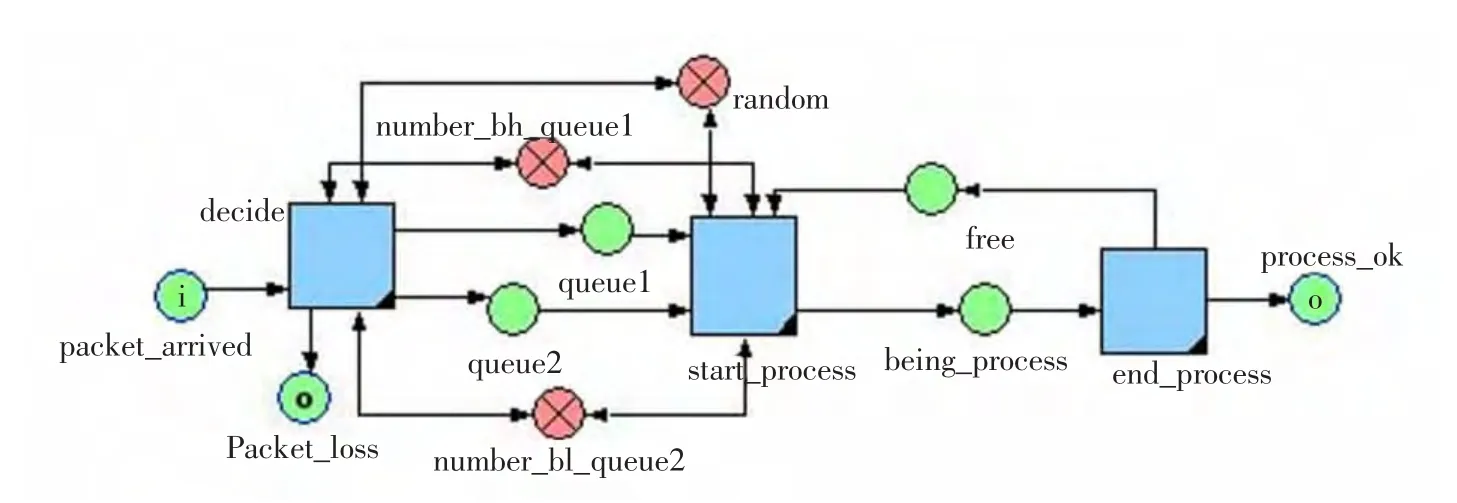
图4 优先级队列缓存管理机制在Exspect中仿真图Fig.4 Simulation diagram of priority queue buffer management mechanism in Exspect

利用仿真软件可得相关的仿真结果。在实际仿真过程中，选取了多组不同的队列容量数据，又分别选取了多组不同的随机处理速率数据，分别进行平均时延和丢包率的测试，并计算吞吐量，再将每组的吞吐量和丢包率进行对比分析，可得传输数据包队列容量、数据包处理速度与吞吐量和丢包率之间的关系，并将仿真结果转化成折线图，见图5和图6。

图5和图6中的Nh和Nl分别为高优先级和低优先级数据报的数量，高、低优先级数据报数量的比例Nh／Nl的不同取值将会对缓存管理机制的性能形成很大的影响，在仿真过程中，将Nh／Nl取在0.5到8之间。图5给出了不同缓存管理机制下数据报平均延迟的对比分析，图6给出了不同缓存管理机制下数据报阻塞概率的对比分析。

3.2 仿真结果分析

图5的实验结果表明，在PQ和IPQ缓存管理机制中，由于高优先级数据报先被转发，所以高优先级数据报的平均延迟要明显低于低优先级数据报的平均延迟，高、低优先级数据报的平均延迟会随着Nh／Nl取值的增加而增加。但由于IPQ缓存管理机制下高优先级数据报也会占用低优先级的缓存队列资源，因此IPQ缓存管理机制下低优先级数据报的平均延迟高于PQ方式，而IPQ缓存管理机制下高优先级数据报的平均延迟低于PQ方式，即IPQ缓存管理机制更能保证高优先级应用的性能。

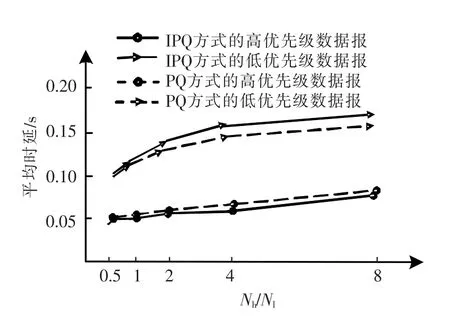
图5 不同缓存管理机制下的平均延迟Fig.5 Average delay in different buffer management mechanism

图6的实验结果表明，在PQ和IPQ缓存管理机制中，随着高、低优先级数据报数量的比例Nh／Nl的增加，低优先级数据报的阻塞概率逐步降低，高优先级数据报的阻塞概率逐步增加。但由于IPQ缓存管理机制下高优先级数据报也会占用低优先级的缓存队列资源，因此IPQ缓存管理机制下高优先级数据报的阻塞概率要低于PQ方式，即IPQ缓存管理机制更能保证高优先级应用的可靠性。

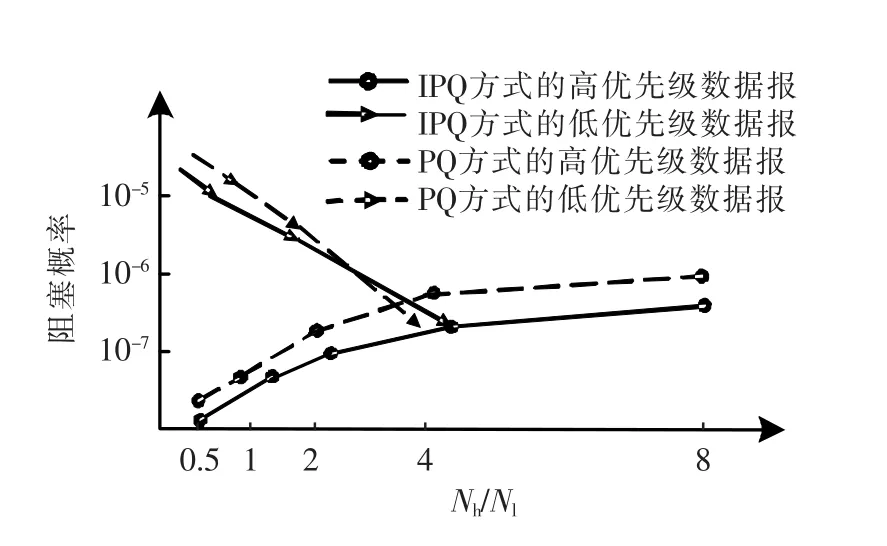
图6 不同缓存管理机制下的阻塞概率Fig.6 Blocking probability in different buffer management mechanism

从图5和图6的仿真实验结果可见，改进的优先级队列（IPQ）缓存管理机制与传统的优先级队列（PQ）缓存管理机制相比，更能保证高优先级数据报的转发速度和可靠性，即多媒体实时数据报的服务质量能够得到保证。

4 结束语

随着多媒体数据的快速增加，网络对延迟和丢包率等性能指标的要求逐渐提高，常规的缓存管理已不能适应当前网络环境的需求。本文基于Petri网并结合排队理论对缓存管理进行了建模并使用Exspect软件进行了仿真与分析。实验结果表明，改进的优先级队列（IPQ）缓存管理机制能够为高优先级的数据报提供更好的服务质量保证，在数据报的平均延迟和阻塞概率等性能指标上有很好的表现，能够更好地满足实时多媒体业务对于服务质量的需求。

［1］ 袁崇义.Petri网原理与应用［M］.北京：电子工业出版社，2005.

［2］ AGHAREBPARAST F，LEUNG V C M.Improving the performance of RED deployment on a class based queue with shared buffer［C］.Globecom，2001：2363－2367.

［3］ BERTSEKAS D，GALLAGER R.Data Networks［M］.北京：人民邮电出版社，2004.

［4］ BEDFORD A，ZEEPHONGSEKUL P.On a dual queueing system with preemptive priority service discipline［J］.European Journal of Operational Research，2005，161：224－239.

［5］ LEFEBVRE D.About the stochastic and continuous Petri nets equivalence in the long run ［J］.Nonlinear Analysis：Hybrid Systems，2011（5）：394－406.

［6］ 蔡令先.基于Petri网政务流程优化及评价方法的研究［D］.大连：大连理工大学，2008.

［7］ LIAN Dawei，ZHAO Xuefeng.Research on the Modeling Method of Production Process of General Assembly of Civil Aircraft based on Petri Network［C］.4th Conference on System Science，Management Science ＆System Dynamics，2010：253－261.

［8］ VAN DER ZEE D J.Building insightful simulation models using Petri nets——a structured approach［J］.Decision Support Systems，2011，51：53－64.